• 信用风险压力测试的核心框架及参数化 [page::1][page::2][page::3]：

- 信用风险压力测试用于内部风险管理与监管，主要通过将过周期（TTC）风险参数（违约概率PD、违约损失率LGD、违约暴露EAD）结合宏观经济模型生成的经济状态因子，将TTC参数转换为点时（PIT）或压力状态风险参数。
- 常见模型基于CreditMetrics框架，采用一因子信用资产模型，利用正常分布变量刻画借款人资产回报，从而推导违约概率及评级迁移矩阵。
- 经济状态z作为宏观经济模型计算得到，通过特定公式将无条件PD映射为经济状态条件PD。

• 过周期（TTC）贷款组合的定义与存在条件 [page::5][page::6][page::12][page::13]:

- TTC组合定义为在无压力条件下，通过迁移矩阵及贷款新发起分布的动态传播过程收敛的唯一稳定组合，与银行当前持仓无关。
- 存在的关键条件：Performing评级子矩阵为primitive（即多周期内评级间彼此可达）；且无新增贷款发起至违约等级。
- 该组合的存在和唯一性由庞加莱-弗罗贝尼乌斯定理保证，且可以利用递归算法计算，且银行当前组合将随着时间趋向此TTC组合。

• 数值实例及虚假违约概率（PD）偏差的风险 [page::7][page::8][page::9][page::10]：

- 采用Trueck和Rachev（2009）公开的迁移矩阵进行计算，结合实际贷款发起分布，得到TTC组合及对应PD。
- 初始组合若与迁移矩阵内隐的TTC组合不一致，组合演变过程中违约概率表现非单调，出现类似“虚假衰退”或“虚假景气”信号，即使无宏观压力输入。
- 该现象在长期演绎中存在，且在一般监管3年压力测试时间范围内即有可能对结果产生显著影响。
- 与TTC组合一致的初始组合演示出合理、平滑的PD趋势，验证模型参数一致性的重要性。

• 实务建议与风险管理启示 [page::9][page::11]：

- 银行应在压力测试前对迁移矩阵及贷款组合进行一致性校验，计算TTC组合并与当前组合比对。
- 通过无压力条件下对组合的多期投影，检查PD及评级分布演变，及时发现潜在模型参数不一致导致的虚假违约率信号。
- 该检测手段有助于识别隐藏的模型偏差，避免压力测试结果误导风险判断，提升压力测试有效性。

金融研究报告详尽分析报告

报告标题： Spurious Default Probability Projections in Credit Risk Stress Testing Models
作者： Bernd Engelmann
发布日期： 2024年1月16日
研究机构： 未明确，但作者为业内资深学者，研究内容涉及银行信用风险压力测试模型
主题： 银行信用风险压力测试模型中的违约概率（Default Probability, PD）投影问题，重点揭示模型参数化导致的伪影（spurious）违约概率预测，尤其对长期情景下信用风险管理的影响。

---

一、元数据与概览

本报告主要针对银行信用风险压力测试模型中的违约概率投影，提出核心论点：当前常用的信用风险压力测试框架中，模型参数的设置蕴含了一个客观上的“穿周期”(Through-the-Cycle, TTC)组合，这个组合是唯一确定且独立于当前银行组合的。银行当前实际的贷款组合在模型框架下，将随时间演化并收敛于这个TTC组合。这一事实会带来潜在的问题，尤其当模型参数与银行当前的组合不符时，会引起违约概率预测的伪影，从而扭曲压力测试的结果。这种情况在银行采用外部数据、跨地区迁移参数或长期气候风险情景模拟时尤为突出。

报告总结了现有模型的基本框架，数学地刻画了这种“TTC组合”的存在性及其计算方法，并辅以数值例证说明问题的严重性和现实意义。作者还建议风险管理者对模型参数和当前资产组合进行必需的验证，防止伪影违约概率对压力测试的干扰。[page::0,1]

---

二、逐节深度解读

1. 引言

介绍压力测试在金融风险管理中的重要性，尤其银行在监管指令（如美联储、欧洲银行管理局）和内部需求下执行的信用风险压力测试。新型压力测试扩展到气候变化相关的长期（30年）情景，带来了更复杂的模型需求。报告点明本研究聚焦在信用风险压力测试的核心参数：违约概率(PD)、违约损失率(LGD)和违约敞口(EAD)，其中违约概率通过评级迁徙矩阵进行建模。这些参数通常基于穿周期视角（TTC），经宏观经济模型转换成即时时点风险参数（PIT），再应用于压力测试。关键指出，在长周期压力测试中，贷款组合动态演化（流失、核销、提前还款、新增发放）及TTC参数定义了一个理想的TTC组合，该组合并非反映银行当前实际状态，而银行组合会逐渐趋向此组合，产生潜在的偏差和伪影。[page::1]

2. 信用风险压力测试模型的框架及基本原理

该节详细阐述了信用风险组合模型的历史起点——1990年代的CreditMetrics框架，并引入一阶因子模型定义单一期限借款人资产收益率分布。资产回报率由系统性因子$Z$和独立特有因子$\epsilon$组成，总体为标准正态分布。违约发生阈值由资产回报率低于$\theta$定义，$\theta$与违约概率$p$的关系通过标准正态分布函数$\Phi$反函数$\Phi^{-1}$确定。系统因子$Z$抽象代表经济状态，负向值增加违约概率，正向则降低。

报告以此推导了条件违约概率$p(z)$公式：

$$
p(z) = \Phi\left(\frac{\Phi^{-1}(p) - \sqrt{\rho}z}{\sqrt{1-\rho}}\right),
$$

这是即时时点评估（PIT）违约概率与穿周期（TTC）违约概率的转化基础。

随后，介绍了基于这一思想的评级迁徙矩阵$\mathbf{T}$的构造，矩阵第$n$个评级为违约吸收态。每个评级对应的迁移概率被阈值分段划分，扩展了单个违约概率的模型。经济状态$z$对迁徙矩阵的影响通过调整阈值实现，从而导出压力测试下的迁徙概率。

最后，结合宏观经济模型，展示如何通过信贷违约率指数$Ct$与宏观经济变量$X{k,t}$的回归，估计经济状态指标$zt$，链接经济模型与迁徙矩阵，完成压力测试风险参数的计算。此部分详细揭示了当前经典信用风险压力测试的模型架构和计算流程。[page::2,3,4]

3. 穿周期组合的数学刻画及唯一性

该节建立了所依据的模型结构假设：贷款组合有$n$个评级等级，初始资产分布向量$W$，给定穿周期迁徙矩阵$\mathbf{T}$及新发放贷款分布向量$O$，并假设有估计好的经济状态时间序列$zt$。每个周期迁徙矩阵根据经济状态更新，组合根据迁徙矩阵演化，同时违约资产立即核销并按比例由$O$向评级重新分配保持总余额不变。

核心结论（定理1）指出：在两个条件下

• （1）构成非违约评级子矩阵$\mathbf{T}p$的若干次幂后所有元素严格正，即矩阵为primitive；

- （2）贷款新增发放不会进入违约评级（$on=0$）；

存在唯一的穿周期组合$W{ttc}$满足组合不变性方程：

$$
W{ttc}^\prime = W{ttc}^\prime \mathbf{T} \mathbf{I}w + (W{ttc}^\prime \mathbf{T} Vw) O^\prime,
$$

且该组合可以通过迭代算法从任意初始组合收敛计算出来。

该节还通过一个简单的反例，证明当条件不满足时不会存在唯一解，展示理论的必要性。作者还从经济角度解释了这些条件的合理性和普适性。[page::5,6]

4. 数值例证与模型参数不一致导致的伪影违约概率

本节对定理1数值求解的过程及结论进行实证演示。采用Trueck和Rachev(2009)的评级转移矩阵$\mathbf{T}$和给定的发放向量$O$，计算得到穿周期组合$W{ttc}$及其整体违约概率约1.198%。

作者设计不同的初始组合$W{init}$，包括与$W{ttc}$较为接近和较为偏离的情形，运行迁徙演化并绘制随年份的违约概率(PD)趋势，发现：

• 初始组合偏离$W{ttc}$时，PD并非收敛单调，而是出现波动，可能先递增后递减或先递减后递增，表现出“伪影”景气或衰退迹象（图1，图2，图3）。

- 这意味着即使未加载真实经济压力（$z=0$），模型自身因参数不一致，仍然会模拟出周期性的假象变化，误导分析和决策。

• 当初始组合与参数模型一致时，违约概率变化平滑收敛，无异常（图4）。

作者强调，实际银行因数据缺乏往往采用外部信用评级机构的迁徙矩阵或跨区域参数，极易出现此类不一致。因此强调参数与组合一致性验证的重要性，并建议在压力测试前进行基础验证：计算$W{ttc}$并与真实组合比对，观察无压力情形下PD曲线，及时发现潜在伪影风险。[page::7,8,9,10]

5. 结论

报告总结指出，信用风险压力测试作为复杂风险管理核心任务，尤其长期压力测试，对参数一致性和精准性有更高要求。普遍采用的迁徙矩阵参数若不匹配银行组合，会导致违约概率的伪影，严重影响压力测试的准确度。

基于理论推导与数值案例，作者明确了穿周期组合的存在及其对全体模型参数及实际组合状态关系的重要性。风险管理人员必须执行基础的参数-组合一致性验证，通过计算TTC组合和无压力演化测试，甄别潜在风险。该简单但科学的步骤可避免或预警模型设计上的错判，从而提升压力测试的稳健性和可靠性。[page::10,11]

---

三、图表深度解读

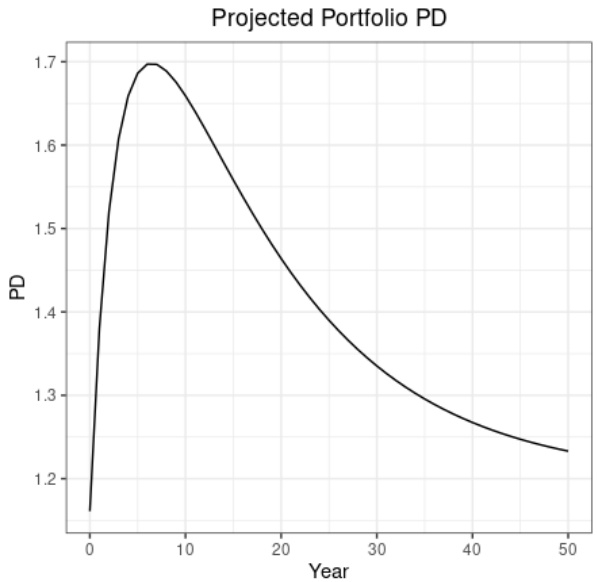
图表1（第8页）— 初始组合为$W{init}$，无经济压力下50年违约概率投影

• 描述：横轴为年份，纵轴为组合平均违约概率（PD %）。初始组合含0权重于最高评级等级，展示了违约概率随时间上升并最终趋于稳定的趋势，部署了非单调路径，有峰值约1.7%。

- 解读：起始组合违约概率为1.161%，略低于TTC组合1.198%。投影初期PD上升，反映组合向参数指定的TTC组合演变过程中资产评级迁移引发违约率上升，模拟出“衰退”假象。

• 关联文本：此图支持章节4对模型不一致时伪影违约概率的分析，说明即便无实际经济压力，模型内置参数也能引发系统性偏差，暗示风险管理中对模型参数与资产状态不符的风险。

- 可能局限性：未显示置信区间或不同情景波动，模型是确定性演示，未考虑市场随机性及估计误差反馈。[page::8]



---

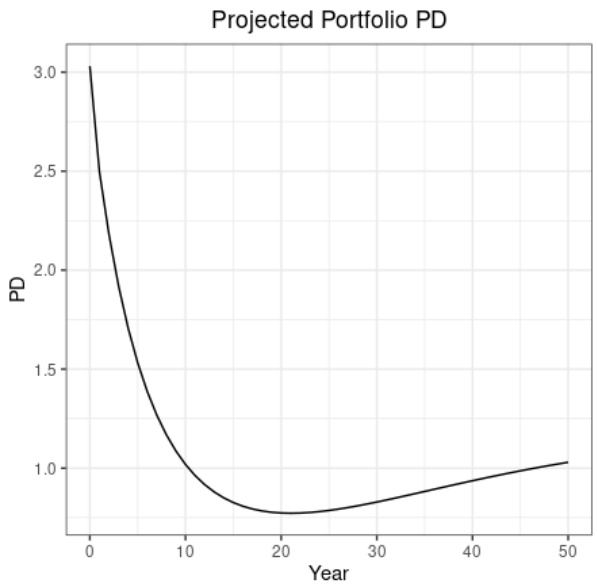
图表2（第9页）— 极端偏离TTC组合的初始组合$\overline{W}{init}$违约概率投影

• 描述：组合初始PD约2.73%，无压力情景下，PD随时间显著下降，最低点约0.72%，之后阶段性反弹并趋于TTC的1.2%附近。

- 解读：初始组合远高于穿周期组合PD，经过迁徙演化过程，模型呈现“假性经济复苏”，违约概率先行下降后缓慢回升，表现出显著非线性和非单调特征。

• 关联文本：说明迁徙矩阵和初始组合错配可能引发模型“假性繁荣”表现，误导风险评估。

- 局限：同样为单路径，无波动性，模拟为确定性过程。[page::9]



---

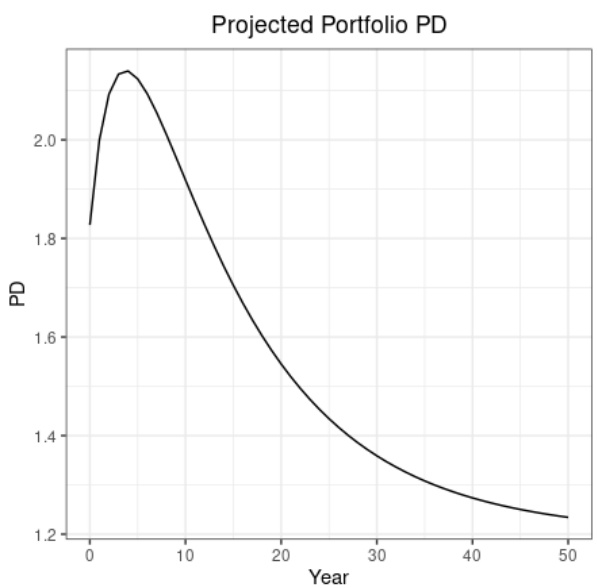
图表3（第9页）— 初始组合$\tilde{W}$中等偏离TTC组合违约概率趋势

• 描述：初始PD 1.83%，投影中PD先升至2.14%的峰值后，缓慢回落收敛至TTC组合1.2%。

- 解读：显示了既非极端也非极端相符的状态下违约率非单调波动，验证伪影违约概率可能先升再降的多变动态。

• 关联文本：强调零权重非唯一成因，而是组合与迁徙矩阵偏离程度及迁徙路径决定PD动态特征。

- 局限同前。[page::9]



---

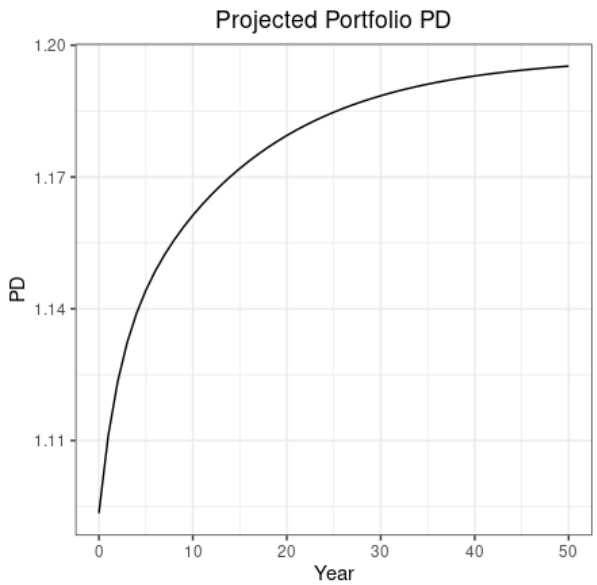
图表4（第10页）— 与参数模型一致初始组合$\hat{W}{init}$的违约概率稳定演化

• 描述：初始组合由压力矩阵作用于TTC组合产生，初始PD 1.093%，投影过程中PD平稳上升，收敛至1.2%左右。

- 解读：违约概率变化平滑无假象波动，验证了模型和组合一致时的预期合理性。

• 关联文本：说明模型一致性是压力测试稳健性基础。

- 局限：无经济压力施加，仅验证一致性效应。[page::10]



---

四、估值分析

本报告属于信用风险管理模型方法研究，未涉及资产价格或公司估值模型，因此无直接估值分析栏目。报告强调的重点为风险参数估计和违约概率投影模型的数学特征和稳定性验证，而非具体资产估值定价。

---

五、风险因素评估

报告隐含的风险主要来自模型参数与银行实际资产组合的不一致：

• 风险表现为“伪影”违约概率波动，投影中出现经济周期假象，使风险管理者对组合风险状况产生误判。

- 风险起因： 迁徙矩阵估计来自异质数据源（外部评级机构、不同地区数据、数据稀缺地区替代），或模型参数与贷款组合特征不匹配。

• 潜在影响： 误判利弊，导致资本要求设定错误，贷款拨备不足或过度，继而影响银行资本稳定及监管合规。

- 缓解措施： 报告建议在压力测试前执行基础验证——计算穿周期组合$W_{ttc}$，比较当前组合，进行无压力条件下违约概率动态演化测试，识别潜在不一致及伪影风险。[page::11]

---

六、批判性视角与细微差别

• 报告基于理论模型假设，实际银行贷款组合和迁徙矩阵估计高度复杂，涉及更多外生因素（回购、担保、违约后恢复等），未完全涵盖在模型中；因此模型简化可能限制适用性。

- 报告强调了TTC组合对当前组合的独立性和唯一性，但在现实中资产迁徙受多重非线性和市场共振影响，模型参数的稳定性和一致性检验也存在方法论挑战。

• 数值案例虽详尽，但缺乏对实际银行数据的验证实例，建议未来研究结合实证数据强化结论。

- 模型动态演化假设总资产保持不变（核销部分新增补充），但贷款余额动态调整和资产质量变化亦可能影响结果，此点未深入讨论。

• 文章对压力期间经济状态$z$的热点建模展开有限，重点放在无压力下的内在伪影，这对现实压力测试的相关性具一定局限。

---

七、结论性综合

本报告针对银行信用风险压力测试中的违约概率投影，揭示了一个关键的模型结构性风险：基于迁徙矩阵和贷款发放参数定义的穿周期贫组合是唯一且模型参数驱动的，独立于当前银行贷款组合。银行实际贷款组合在无经济冲击情况下，会逐步迁移并收敛至该穿周期组合。

由于迁徙矩阵参数通常基于外部或非匹配数据估计，实际贷款组合与模型内置穿周期组合往往存在显著差异。正是这种不一致导致无压力条件下违约概率曲线表现出明显的非单调波动，模拟出“假象”经济衰退或繁荣周期。如此伪影若忽视，将严重误导压力测试结果，从而影响资本充足度评估和风险拨备。

作者通过数学理论证明穿周期组合的存在性和唯一性的条件，凭借数值模拟强化论点，强调风险管理必须对模型参数与真实资产组合进行一致性验证。建议计算穿周期组合并以无压力演化模拟验证参数合理性，及时发现潜在伪影，以保障压力测试结论的正确性。

概括而言，报告主张的关键立场是：信用风险压力测试的准确性核心，在于确保模型参数与银行当前资产组合的一致性，规避违约概率的伪影投影，从而保证风险识别的稳健性和资本配置的精准性。该观点对长期气候风险压力测试等新型压力测试尤为重要。[page::0-11]

---

总结

本报告从理论、模型、数值及风险管理实践角度，全面并深刻揭示了信用风险压力测试中参数模型和资产组合不一致性导致的违约概率投影伪影问题。对风险管理者在压力测试建模与使用过程中具重要警示和指导作用，尤为提醒了跨数据来源组合和长周期压力测试时的潜在陷阱和必要检验环节。报告内容严谨、条理清晰、结合数学推导与实际案例，具备较强的实务价值和理论贡献。

报告