• ITU模型定义及动机 [page::0][page::1]：

- 完全可转移效用(TU)假设转移效用以恒定“兑换率”转移，而ITU考虑可能存在非线性转移限制，如税收或非线性公共物品分配，且无法统一标度转换。
- 例子覆盖劳动市场工资税收模型与婚姻市场对私人和公共消费的分配等。

• 四种经典效用模型及其距离前沿函数描述 [page::2][page::6][page::8][page::9]：

| 模型 | 特性 | 距离-前沿函数示例 |
|---|---|---|
| TU | 效用完全线性可转移，Pareto前沿为线性 | $D{ij}(u,v)=\frac{u+v-\Phi{ij}}{2}$ |
| NTU | 不可转移，效用独立上限 | $D{ij}(u,v)=\max\{u-\alpha{ij}, v - \gamma{ij}\}$ |
| LTU | 工资税率引入倾斜的线性边界 | $D{ij}(u,v)=\frac{\lambda{ij}u+\zeta{ij}v - \Phi{ij}}{\lambda{ij}+\zeta{ij}}$ |
| ETU | 指数型工具实现非线性Pareto边界 | $D{ij}(u,v)=\tau{ij}\log\left(\frac{e^{\frac{u-\alpha{ij}}{\tau{ij}}}+e^{\frac{v-\gamma{ij}}{\tau{ij}}}}{B{ij}}\right)$ |

• 结合集合交/并运算生成复杂模型 [page::7][page::9]：

- 使用距离-前沿函数的最小/最大操作对应可行集合的并/交集，有助于组合税率分段及公共物品离散选择问题。

• 匹配稳定性条件及均衡定义 [page::11][page::13]：

- 个体匹配稳定性定义：匹配变量$\mu{ij}\in\{0,1\}$满足配对边界条件$D{ij}(ui,vj)=0$（匹配时）及稳定约束$D{ij}(ui,vj) \ge 0$（任意配对）。
- 引入异质性及未观测偏好的结构化模型，假设效用可分解为系统效用+随机扰动，满足支持全域和连续性。
- 提出聚合均衡定义，匹配与系统效用依赖效用风差（wedge）$W{xy}$，满足市场供需清算。

• 均衡存在性与唯一性及算法解法 [page::14][page::15]：

- 存在唯一价格向量$W$使供需过剩函数为零，采用Jacobi方法基于大类替代性质进行迭代收敛。

• ITU-logit模型及匹配函数均衡 [page::16][page::17]：

- 假设扰动为Gumbel分布，系统效用与匹配量满足对数奇数比关系。
- 匹配数$\mu{xy}$与剩余单身量$\mu{x0},\mu{0y}$通过特定距离函数生成匹配函数$M{xy}$相联系，包含TU、NTU及LTU、ETU的特殊形式。
- 匹配函数均衡通过非线性方程组求解，算法2为对应交替逼近方法，收敛至唯一解。

• 参数估计方法 [page::18][page::19]：

- 基于参数化距离函数的最大似然估计，推导相应对数似然函数及其梯度，利用样本匹配数据估计模型参数。

• 规范性及经济学性质分析 [page::20][page::21][page::22][page::23]：

- 探讨匹配的正相关性条件推广至ITU。
- 使用Legendre-芬谢尔变换将系统效用与匹配量联系，实现仅用匹配量描述的均衡定性。
- 比较静态分析揭示人口变化如何影响匹配结构与个体福利，验证Becker关于伴侣相对稀缺性的预期。
- 探讨均衡与最优解的关系：TU下两者一致，ITU下一般不等价。

• 扩展及相关领域讨论 [page::24][page::25][page::26][page::27][page::28][page::29][page::30][page::31]：

- 赋予与公平性（同质个体等遇）、Pareto效率、非凸集合交并及多对一匹配的理论归纳。
- 讨论模型的存在性多种证明路径及其与传统匹配理论的关联。
- 植入具有搜索摩擦的动态匹配框架，实现ITU版本的Shimer-Smith模型推广。
- 浅述相关文献，包括TU、NTU与ITU匹配模型以及经济学婚姻市场和劳动力市场经验研究。

• 核心图示强化模型理解

- 图示阐释非凸有效集与随机化假设之权衡，以及Pareto效率与Pareto权重法的区别。

金融研究报告详尽分析报告

——《Matching under Imperfectly Transferable Utility》章节草稿解构与深度解析

---

1. 元数据与报告概览

• 标题：《Matching under Imperfectly Transferable Utility》（不完美可转移效用下的匹配）

- 作者：Alfred Galichon 与 Simon Weber

• 发布机构：《Handbook of the Economics of Matching》经济学匹配手册（编辑：Che, Chiappori 和 Salanié）

- 日期：2024年10月4日

• 研究主题：探讨匹配市场中效用不可完全转移（Imperfectly Transferable Utility，ITU）的框架，拓展传统可完全转移效用（Transferable Utility，TU）模型，同时构建并推导ITU模型的理论基础、均衡特征及应用。

核心论点：

• ITU模型是对传统TU模型的有意义扩展，尤其中在存在转移限制（如税收影响）或效用转移非线性时，它更符合现实经济匹配市场情形。

- 提出并界定以“距离到前沿函数（distance-to-frontier function）”为核心工具的ITU模型数学表示，适用于广义匹配模型。

• 设计了匹配函数（matching functions）及均衡存在性和唯一性的数理证据，特别是在考虑异质性的宏观匹配市场中。

- 在控制异质性、无完全效用转移背景和logit偏好假设下，给出了逐步计算算法与极大似然估计方法。

[page::0,1,2]

---

2. 章节详解

2.1 引言与动机（1. Introduction）

• 论点：介绍ITU模型的必要性。现实中转移效用因各种市场摩擦和非线性因素无法百分百转移，如工资税收、家庭中的资源分配。TU模型虽然简洁，但过于理想化。

- 定义：效用分配集合$\mathcal{F}{ij}$的形态由函数$A{ij}$和$B{ij}$控制，不再是简单线性组合的形式。ITU可视为一类更广义的转换技术。

• 关键辨析：ITU与TU最大差别在于匹配市场中关于不同潜在匹配对象无法统一公度化的效用分割尺度——这导致ITUs下均衡结构更为复杂且具现实意义。引用Chiappori 2017强调TU模型中恒定“交换率”假设的局限。

[page::0,1]

2.2 符号与模型设定（1.2 Setting and notations）

• 个体层面：考虑男女配对的异性恋市场，匹配变量$\mu{ij}\in\{0,1\}$，满足匹配可行性条件（最多单配不重叠）。

- 类型层面：引入$|\mathcal{X}|$男类型与$|\mathcal{Y}|$女类型定义，记人数规模$nx,my$，并允许单身作为类型0。

• 宏观匹配：匹配向量$\mu{xy}\ge0$，满足量的容量限制（匹配质量不超量），并定义内点匹配集$\mathcal{M}^0$。

此设定奠定了后续理论推导的基础，强调了匹配的有限容量与类型层面分布。

[page::1]

2.3 ITU案例示范（1.3 A bestiary of models）

• 示例1（平税）：公司支付给工人的工资受单一税率$\tau{ij}$影响，导致工人与公司实得/支付效用不等，Pareto前沿变为线性但斜率非-1。

- 示例2（累进税）：工资分段课税，产生分段线性前沿，整体Pareto集合为多个线性集合的交集。

• 示例3（婚姻市场的私有消费）：夫妻分配总预算于各自私有消费，效用呈对数形式，Pareto前沿非线性，且与福利参数相关。

- 示例4（加公共物品）：夫妻决策公共物品投入，导致Pareto集合为多个非线性子集的并集，非凸，表达更复杂。

以上示例扩展了ITU框架适用范围，覆盖税制、消费分配与公共物品，多层次非线性结构体现效用转移的复杂现实性。

[page::2,3]

2.4 配对讨价还价集结构（2. Pairwise bargaining sets）

• 详述效用讨价还价集$\mathcal{F}{ij}$的形式，以及Pareto效率前沿与常用的加权Pareto权重方法的异同。指出在非凸集合中两者可能不同，常见模型若假设随机化决策则相当于凸化集合，但现实中随机化假设难以接受。

- 作者支持纯粹的Pareto效率路径而非权重均衡，强调竞争市场均衡决定在哪个Pareto点达成效用分配。

下文定义了proper bargaining set的三条性质：

• 闭合非空，

- 下方完备性（满足自由处置条件），

• 上界有界性（防止无穷效用）。

通过图示（图2）展示不同匹配集形态：TU简单线性，NTU矩形，LTU线性斜率变更，ETU非线性等。

[page::3,4,5,6]

2.5 距离到前沿函数（Distance-to-frontier function）

• 定义距离到前沿函数 $D{\mathcal{F}{ij}}(u,v)$为从效用点$(u,v)$沿对角线偏移至效用集边缘的最小移位量，作为匹配集的隐式表示。

- 证明距离函数具备单调性、连续性，且集合并、交对应距离函数的取最小与取最大操作（Lemma 2），为多元、复杂匹配集构造提供算术工具。

• 应用示例2、4中的分段与并集形式，均由对应距离函数的最大或最小表述可构成。

[page::7]

2.6 各类模型距离函数重述（2.4 Examples）

• TU模型: $\mathcal{F}{ij}=\{u+v \le \Phi{ij}\}$, 距离函数线性并为$\frac{u+v-\Phi{ij}}{2}$。

- NTU模型: $\mathcal{F}{ij}=\{u \le \alpha{ij}, v \le \gamma{ij}\}$，距离函数为$\max\{u-\alpha{ij}, v-\gamma{ij}\}$。

• LTU模型（自身税率引入）: 集合定义为线性约束$\lambda{ij} u + \zeta{ij} v \le \Phi{ij}$，距离函数相应调整。

- ETU模型（对数效用与预算共享）: 集合定义为指数和不超过预算，距离函数为对数形式。

• 分段LTU模型（示例2累进税）: 距离函数为各个线性距离的最大值，体现分段线性组合。

- 分布式ETU模型（示例4公共物品）: 距离函数为各公共物品量下距离的最小值，即复合集合以距离操作并接。

• 引入不确定性模型: 若分配变量随机且效用为VNM效用，则效用前沿非线性凸，体现ITUs特性。

这些例子表明distance-to-frontier函数对多样化匹配机制具备强大的描述能力。

[page::8,9,10]

2.7 稳定匹配定义与特征（3 Stable matchings without heterogeneity）

• 定义个体均衡结果（individual equilibrium outcome）三元组$(\mu{ij}, ui, vj)$满足匹配可行性、讨价还价前沿约束、个体保障效用（reservation utility）及互补松弛条件。

- 证明$D{ij}(ui,vj) \ge 0$（配偶非匹配状态下效用不可在集合内部否则会破坏稳定），匹配时则恰等于0。

该定义是ITU稳定匹配的非线性推广，定位等同于TU情形中的最优匹配条件。

[page::11]

2.8 带异质性的宏观均衡（4 Stable matchings with heterogeneity）

• 假定具有可观测分类型异质$x \in \mathcal{X}, y \in \mathcal{Y}$及随机无观测异质（idiosyncratic preference shocks）$\epsilon, \eta$，其中个体效用含系统部分与随机部分叠加。

- 关键假设：
- 无观测异质的分布具有覆盖全$\mathbb{R}^k$的密度（非零、绝对连续支持），确保均衡匹配的独特性及存在性。

• 引入表现出受价差$w = u-v$参数化的效用前沿函数$\mathcal{U}{\mathcal{F}{xy}}(w)$和$\mathcal{V}{\mathcal{F}{xy}}(w)$，满足边界条件及一致性。

- 提出aggregate equilibrium outcome定义，要求：
- 匹配内点且严格可行，
- 系统效用满足距离为零的边界条件，
- 匹配与系统效用满足市场均衡条件（供需平衡，表现为最大期望效用对应的匹配数量相等）。

• 通过离散选择模型（max-utility选择）将匹配问题拆解为“供给-需求”关系，利用Daly-Zachary-Williams定理求出匹配质量。

[page::12,13,14]

2.9 存在唯一性与计算方法（4.4 Existence, uniqueness and computation）

• 定义超额需求函数 $Z(W)$（价格向量$W$为市场价差$w$）：供需差，通过利用效用前沿函数的梯度$\nabla G, \nabla H$表示。

- 基于gross substitutability性质（价格升高使当商品需求降低，替代品需求上升）证明$Z(W)=0$解的存在与唯一性（Theorem 1）。

• 提出Jacobi迭代算法（Algorithm 1）：初始化高价使超额需求为负，递归更新价格直到超额需求趋近零，实现数值解法。

- 通过逆单调性（inverse isotone）证明唯一性的严谨性。

[page::14,15]

2.10 ITU-Logit模型与匹配函数（5 The ITU-logit model）

• 在偏好异质服从Gumbel（logit模型）假设下，配对效用易求解析表达式，即通过log-odds-ratio给出系统效用：

$$
U{xy} = \log \frac{\mu{xy}}{\mu{x0}}, \quad V{xy} = \log \frac{\mu{xy}}{\mu{0y}}
$$

• 结合效用集约束，导出匹配函数关系：

$$
\mu{xy} = \exp\left(-D{xy}(-\log \mu{x0}, -\log \mu{0y})\right)
$$

匹配函数定义了配对数量与剩余单身的内生联系，仍属于均衡方程式。

• 对应用模型匹配函数举例：

- TU-logit: $M{xy} = \mu{x0}^{1/2} \mu{0y}^{1/2} e^{\Phi{xy}/2}$
- NTU-logit: $M{xy} = \min\{\mu{x0} e^{\alpha{xy}}, \mu{0y} e^{\gamma{xy}}\}$
- LTU-logit与ETU-logit模型对应的匹配函数通过参数权重份额以相似形式表达，且ETU为NTU与TU的极限形式。

• 定义匹配函数均衡（matching function equilibrium），通过终端单身数$\mu{x0}, \mu{0y}$和匹配函数系统方程求解整体均衡匹配。

- 提出迭代算法（Algorithm 2）用于解此非线性系统，证明其收敛且与Gale-Shapley延迟接受算法机制具类似递减递增福利特性，为连续版本。

[page::15,16,17]

2.11 参数估计（6 Estimation）

• 假定距离函数$D{xy}$属于参数化族 $D^{\lambda}{xy}$，参数$\lambda$待估计。

- 利用匹配数据样本，构造样本匹配频率$\hat{\pi}{xy}$及极大似然函数：

$$
l(\lambda, u, v) = -\left(\sum{xy} \hat{\pi}{xy} D{xy}(\lambda,u,v) + \sumx \hat{\pi}{x0} ux + \sumy \hat{\pi}{0y} vy + \log N(\lambda,u,v)\right)
$$

其中$N(\lambda,u,v)= \sum{xy} e^{-D{xy}(\lambda,u,v)} + \sumx e^{-ux} + \sumy e^{-vy}$归一化匹配概率。

• 一阶条件、得分函数及Fisher信息矩阵均得以表述，使MLE标准统计推断成为可能。

- 设计算法进行参数估计，且在样本容量大时满足渐近正态。

[page::18,19]

2.12 规范性与经济属性（7 Remarks and discussions）

• 正向配合匹配（Positive Assortative Matching，PAM）：ITU模型中PAM由偏导及Spence-Mirrlees条件推广决定，TU案例特例。

- 均衡表达式简化分析：利用Legendre-Fenchel变换将市场均衡条件表示为边际函数导数零点问题，减少引入复杂潜变量。

• 比较静态分析（Theorem 4）：总人口变化如何影响匹配数量及效用分配，验证经典Becker观点（人口结构影响婚姻市场）。

- 均衡解区分：ITU情形下跨性别福利偏导无对称性，TU情形则对称性成立，提供可检验假设。

• 均衡与最优解差异：TU模型均衡与最优配送一致，ITU由于非线性转移，均衡不可简化为福利最大化（缺乏优化问题的对偶结构）。

- 异质性缺失情形：利用互补松弛条件与顶点算法证明均衡存在性与唯一性。

• 平等待遇与效率性：

- 当$D{ij}(u,v)$严格单调时有人物福利差异必引发匹配破裂，实现平等待遇。
- 否则如NTU模型则平等待遇非必然，但染模设计倾向于实现该属性。

• 扩展：

- 一对多匹配模型，考虑公司雇佣多工人包。
- 有/无完整匹配、单身选项差异。

• 非可转移效用模型：允许“效用燃烧”，即匹配稳定态非必然是联合最大效用的状况，解释市场浪费以及工人过剩时的挣扎竞争。

- 搜索与匹配框架：与Shimer-Smith连续时间匹配模型扩展至ITU设定，考虑动态匹配、拆散率与折现率，给出Bellman方程和匹配条件。

[page::20,21,22,23,24,25,26,27,28,29]

2.13 相关文献综述（8 Related literature）

• 图谱清晰呈现TU、NTU与ITU匹配理论发展史，包含重要贡献者及代表文献。

- 介绍ITU匹配存在性、均衡结构的算法性证明，包含Kelso-Crawford、Hatfield-Milgrom等研究。

• 强调最近关于效用前沿距离函数与市场均衡存在唯一的新发现和应用。

- 实证框架方面，ITU较TU与NTU文献更稀缺，Galichon等人的研究为开创者。

• 婚姻市场、劳动市场的研究动态，如何将集体家庭决策模型与ITI匹配框架串联。

- 算法实现参见Sinkhorn/IPFP法及其扩展，呈交叉学科的数学经济学谱系。

[page::30,31,32,33]

---

3. 图表与数据解读

图1：家庭中公共物品选择的匹配集可行域示意

• 内容说明：图示展示了公共物品选择导致的匹配效用集合$\mathcal{F}_{ij}$并非凸集，前沿存在黑色曲线（Pareto边界）和红色凸壳边界（凸集前沿）。

- 数据趋势与解释：
- 红色线对应Pareto权重法可达前沿，黑色曲线表明部分Pareto效率点不可由权重法达到，强调纯效率视角上的市场均衡必要性。
- 反映选择“买”或“租”住房决策的非凸效用集，凸显市场不连续性、非线性影响。

• 联系文本：支持2.1节中对Pareto效率和权重分配方法的理论批判，呈现实证直观。

- 方法局限：随机化假设（凸化）行为在经济上难以合理化。

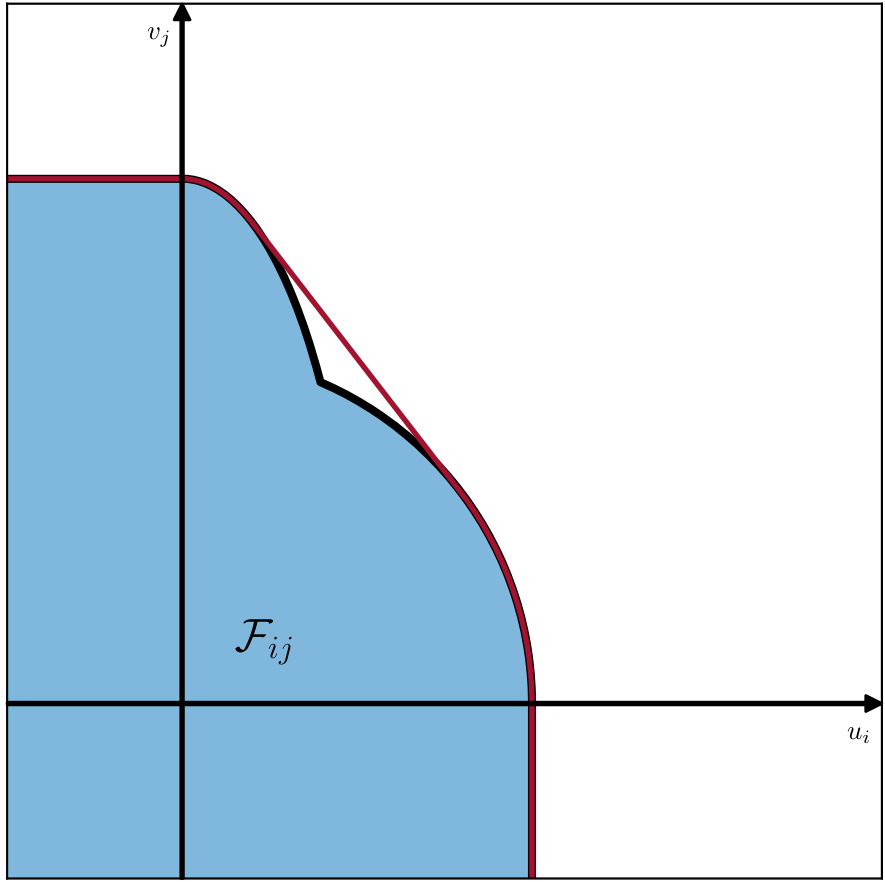
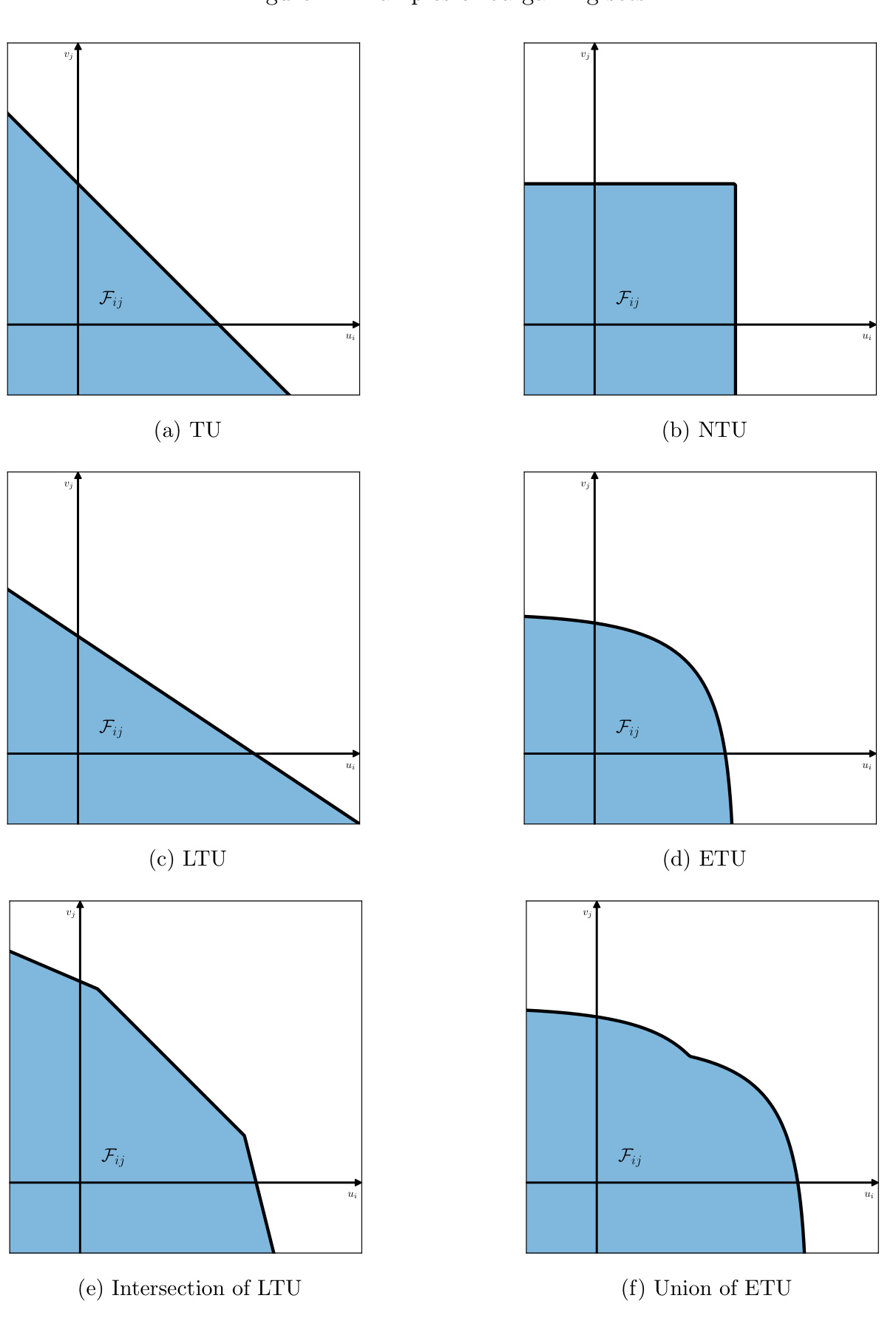
图2：不同匹配模型的效用集结构（子图a-f）

• 内容说明：展示TU、NTU、LTU、ETU及其复合模型对应匹配效用的可行域形态。

- 数据趋势与解释：
- TU（a）为标准线性拼接，完备且凸。
- NTU（b）为矩形，非凸，效用不能转移。
- LTU（c）为倾斜线性，体现部分线性转移。
- ETU（d）为凸非线性曲线，体现私有消费对数效用。
- 交集LTU（e）及并集ETU（f）表现复杂不凸或分段形态。

• 联系文本：图形化阐明2.4节理论模型匹配集性质，有利于直观理解模型多样性。

- 底层数据：由参数$\lambda,\zeta,\alpha,\gamma,\tau$控制，体现税收、消费结构、公共物品影响的经济机制。



---

4. 估值分析

本章节核心在于介绍匹配模型推导的稳健均衡价格（效用差）向量$W$的求解机制。通过定义excess demand function $Z(W)$，利用均衡条件$Z(W)=0$确定市场均衡解。

• 估值本质是找出一组均衡价格$W$，使得匹配需求和供应平衡。

- 该方法属于非线性（凸）规划范畴，满足gross substitutability条件，保证雅可比迭代算法局部收敛与唯一性。

• 迭代算法为求解配对价格提供了实际可操作的框架，适合大规模求解。

- Estimation部分将距离函数参数化，构造基于匹配频率的极大似然函数，参数估计及其渐近性质具备理论保证，方便计量分析。

• 与传统TU模型相比，估值中更强调距离函数的非线性与多样性，适用范围更广。

整个估值框架拥有较强的理论推导基础，适合应用于多样化劳动和婚姻市场建模。

---

5. 风险因素评估

报告整体未直接将风险定义为特定章节，但隐含风险主要体现为：

• 模型假设风险：

- 转移效用假设的适用范围有限，实际税收、家庭决策行为复杂，过于简化模型可能失真。
- Pareto效率假设放弃了权重分配方案，隐含个体策略随机化可能风险（现实中随机化难成立）。

• 均衡唯一性风险：

- 需满足gross substitutability、无观测异质性支持等假设，否则可能无稳定解或多重均衡。

• 数据和估计风险：

- 参数化假设、数据完整性、异质性分布的正确性直接影响估计准确。
- 估计方法依赖于充分样本和模型正确定义，偏误或异方差可能导致估计失效。

• 动态匹配和市场摩擦风险：

- 章节7.10涉及的搜索匹配模型假设较多，随机匹配抵消、匹配报酬的动态变化可能导致实际市场稳定性欠佳。

报告较透彻地对隐含风险表述较为谨慎，未给出完善缓解策略，但通过严格条件保证理论稳健性，暗示模型实际应用时需谨慎进行条件检验。

---

6. 批判性视角与细微差别

• 模型偏好：

- 作者偏向使用的Pareto效率路径放弃了随机化或权重方案，可能忽略了现实中多样协商的可能性，限制了模型适应性。

• 非凸匹配集处理：

- 作者强调非凸结构的不可忽视性，批判对模型凸化并随机化的常规方法，但从实用角度看，凸化能极大简化计算，权衡取舍欠缺讨论。

• 等价转换与尺度问题：

- ITU效用尺度转化无法统一，强调不同匹配对的不可比性，可能导致模型对尺度选取敏感，估计复杂。

• 无观测异质性的强假设：

- 全支持和密度非零假设强烈，实际市场个体偏好分布可能难以完全满足。

• 算法复杂度与实际适用性：

- 虽有迭代算法保证收敛，但高维匹配市场和一对多组合匹配存在计算瓶颈，报告未详述实际规模上的实施问题。

• 非凸ITUs市场均衡对优化性缺失：

- 等价于失去了社会福利最大化的保障，部分经济学家可能质疑该点对政策分析的适用性。

综上，报告在理论创新和严密性上有所突破，但对实用操作性及市场多样性复杂性的包容性偏弱，尤其对非凸效应的经济解释尚需深入。

---

7. 结论性综合

该章节草稿详尽系统地展现了不完美可转移效用匹配模型的系统理论, 其贡献点包括：

• 在转移效用可转化性受限的现实环境下提出更为严谨的模型体系和参数化方法，填补了匹配市场建模长期以来的理论空白。

- 通过距离到前沿函数，提供了描述复杂匹配效用集的统一工具，使得包含税收、中间消费、公共物品以及不确定性的效用模型均可纳入框架。

• 发展了配对讨价还价集对应的距离函数代数计算规则（取最小、最大），允许复杂组合模型的构建与解析。

- 明确界定了纯粹的Pareto效率路径匹配均衡，批判了既有的权重分配及凸化随机化处理假设，强调市场均衡端点的内生性。

• 展示了异质性匹配中个体与聚合均衡结果的对应关系，证明了存在唯一均衡及提供了有效数值迭代算法（Jacobi和迭代比例拟合）。

- 对于带logit异质性的ITU模型，提出了对应的闭式匹配函数表达和均衡求解算法，使拟合估计成为可能。

• 从理论到计算，从微观个体到宏观匹配结构，覆盖了协调、估值、风险、优化性等多个维度，提供了极具操作意义的匹配市场分析体系。

- 结合丰富的经济学实例（劳动市场、婚姻市场、公共物品决策）和现实经济现象（进税累进性、不确定性、家庭福利分配），形成理论与实践良性循环。

• 系统地回顾了匹配经济学中TU、NTU、ITU模型的演进及其现实适用边界。

从图表深度分析来看，文本对不同匹配集形态及公共物品决策的非凸性进行了形象展现，直观提升了理论洞察力。匹配函数和综合均衡条件的迭代算法为实务应用提供了强有力的工具。

总之，作者传达的核心判断是：

通过引入和系统刻画不完美可转移效用，能够更贴切地描述真实匹配市场的效用约束和交易结构，同时保留并延伸了传统一可转移效用模型的稳健均衡理论和可计算性，实现理论的质的飞跃。

---

参考页码

[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]

---

以上即对该章节草稿的全面解析，涵盖理论结构、数据/图形解读、估值、风险、批判及综合结论，深入展现了报告的重要观点及其整体经济学意义。

报告