• 研报提出了鲁棒稀疏均值-方差（RSMV）模型，融合椭球型不确定集降低参数估计误差影响，同时引入固定交易成本惩罚过度分散，[page::0][page::2]

- 理论证明RMV组合可分解为最小方差组合与均值-方差组合凸组合，风险厌恶系数$\kappa$与不确定性水平$\varepsilon$一一对应，为风险参数选择提供理论指导 [page::5][page::6]

• 在高参数不确定性下，鲁棒组合逐渐趋近均等权组合，确认鲁棒性带来投资偏好向简单分散策略转变 [page::8][page::9]

- “分散悖论”: 通过参数化协方差矩阵，揭示不确定性与交易成本交互作用下，持仓资产数量可增减或保持不变，短暂增加不确定性甚至可能减小持仓，验证模型对真实市场多样化现象的解释力 [page::10][page::11]

• 研发半光滑牛顿法结合差分-凸函数算法（SN-pDCA），解决NP难的稀疏组合优化，具有局部线性收敛率，显著提升大规模优化效率，适用于逾千资产规模 [page::12][page::13][page::16][page::17][page::18]

• 数值实验基于Fama-French、标普500及Russell 2000美股数据集，SN-pDCA算法相较CPLEX与传统$\ell_1$方法，在目标函数值、稀疏性和计算时间均表现优越；加速版本Ac-SN-pDCA表现更佳[page::20][page::21]

• 大规模数据（326至1074资产）中，SN-pDCA算法能在分钟级完成求解，而CPLEX难以在限定时间内收敛，验证算法实用性与扩展能力[page::21][page::23]

| Dataset | CPLEX Obj. | SN-pDCA Obj. | Ac-SN-pDCA Obj. | L1MV Obj. | CPLEX Card. | SN-pDCA Card. | Ac-SN-pDCA Card. | L1MV Card. | CPLEX Time (s) | SN-pDCA Time (s) | Ac-SN-pDCA Time (s) | L1MV Time (s) |
|---------|------------|--------------|-----------------|-----------|-------------|---------------|------------------|------------|----------------|------------------|---------------------|---------------|
| FFInd12 | 0.0385 | 0.0398 | 0.0398 | 0.0413 | 4 | 5 | 5 | 6 | 0.17 | 0.11 | 0.11 | 0.11 |
| FFInd17 | 0.0366 | 0.0379 | 0.0379 | 0.0400 | 2 | 4 | 4 | 6 | 0.26 | 0.13 | 0.15 | 0.11 |
| SPX326 | 0.0405 | 0.0404 | 0.0401 | 0.0646 | 5 | 13 | 12 | 38 | 600 | 1.97 | 1.80 | 1.97 |
| RUT500 | 0.0919 | 0.0821 | 0.0797 | 0.0981 | 8 | 23 | 16 | 35 | 600 | 1.84 | 1.70 | 1.60 |

• 计算结果证实，在固定交易成本下，资产不确定性提升可能导致持仓资产数量递增、递减或稳定，体现出模型对“分散悖论”的刻画能力，提供策略调节依据 [page::24]

报告详尽分析报告——《Robust and Sparse Portfolio Selection: Quantitative Insights and Efficient Algorithms》

---

一、元数据与报告概览

• 报告标题：《Robust and Sparse Portfolio Selection: Quantitative Insights and Efficient Algorithms》

- 作者：Jingnan Chen, Selin Damla Ahipasaoglu, Ning Zhang, Yufei Yang

• 机构：北京航空航天大学经济管理学院、南安普顿大学数学科学院、东莞理工大学计算机学院、新加坡科技设计大学等

- 发布时间：报告未明示具体发布日期，但数据和算法背景属于较近时期

• 主题领域：投资组合理论，特别是均值-方差（mean-variance, MV）框架下的稳健（Robust）与稀疏（Sparse）投资组合优化，算法设计与数值实验

- 核心论点：
- 该报告提出了稳健稀疏均值-方差（RSMV）模型，将估计误差考虑为椭球不确定集，并通过固定交易成本引入组合稀疏性以避免过度分散；
- 该模型兼具理论深度和计算实用性，作者设计了基于半光滑牛顿法的近端差分凸算法（SN-pDCA）高效求解该复杂的混合整数优化问题；
- 以此深入阐述了风险厌恶系数、估计参数不确定性与交易成本三者之间的相互关系，对组合权重的分散度产生重要影响；
- 数值实验证明该算法比传统混合整数规划求解器效率更高、结果更优，且RSMV模型对经典MV模型进行统一推广。

• 目标读者：金融工程、运筹优化、应用数学领域的研究人员与实务投资组合管理者

---

二、逐节深度解读

1. 引言（Introduction）

• 关键点概述：

- 传统Markowitz MV框架促进多元分散以降低投资组合波动，缓解估计风险；
- 过度分散存在问题（“多元分散悖论”），导致实际收益不足，部分经验丰富投资者选择集中配置（如巴菲特所言优先配置最优资产）；
- 提出在稳健优化基础上引入固定交易费用实现组合稀疏性的RSMV模型，旨在寻找分散与集中之间的平衡。

• 推理与假设：

- 组合权重表示为向量$\mathbf{x}$，资产收益的估计不确定性用椭球集限定资产收益$\mathbf{r}$，交易成本$\phi$通过指示函数对非零权重项惩罚；
- 约束集为$\mathcal{C}=\{\mathbf{x}:\mathbf{e}^T \mathbf{x}=1 \}$，保证资金完全投入。

• 公式（RSMV模型）：

$$
\min{\mathbf{x} \in \mathcal{C}} \max{ \mathbf{r} } \kappa \mathbf{x}^T \Sigma \mathbf{x} - \mathbf{r}^T \mathbf{x} + \phi^T \mathbb{1}(\mathbf{x}) \quad \text{s.t.} \quad (\mathbf{r} - \bar{\mathbf{r}})^T \Omega{\bar{\mathbf{r}}}^{-1}(\mathbf{r} - \bar{\mathbf{r}}) \leq \varepsilon
$$

$\kappa$为风险厌恶系数，$\varepsilon$为不确定集大小。

2. RSMV模型及稳健效应（Robust and Sparse MV Portfolio Optimization）

• 关键论述：

- 估计误差主要体现在收益均值，因而引入椭球形不确定集对$\bar{\mathbf{r}}$进行区间限定；
- 固定交易成本$\phi$用于模型稀疏化，避免过度分散中的小额头寸；
- RMV（稳健MV）模型是RSMV的零交易费用特例，能够用两个基准组合（MV组合和最小方差组合MIN）凸组合表示；
- 证明风险厌恶系数$\kappa$与不确定集大小$\varepsilon$存在一一对应关系，即调整$\kappa$相当于调整$\varepsilon$，通过改变量化投资者的稳健程度。

• 关键公式及数据点：

- RMV模型简化形式：

$$
\min{\mathbf{x} \in \mathcal{C}} \kappa \mathbf{x}^T \Sigma \mathbf{x} + \sqrt{\varepsilon} \sqrt{\mathbf{x}^T \Sigma \mathbf{x}} - \bar{\mathbf{r}}^T \mathbf{x}
$$

• 命题解析：

- 命题1：RMV最优解为MV组合和MIN组合的凸组合，权重依赖于$\rho^(\varepsilon)$（单调递减函数）；

$$
\mathbf{x}{RMV} = \frac{\kappa \rho^(\varepsilon)}{1 + \kappa \rho^(\varepsilon)} \mathbf{x}{MV} + \frac{1}{1 + \kappa \rho^(\varepsilon)} \mathbf{x}{MIN}
$$

说明当不确定性$\varepsilon$趋近于0时，RMV趋近于MV组合，反之趋近于MIN组合，反映投资者在不确定性增加时更偏好低风险组合。

- 命题2：$\kappa=0$时的极端情况下，RMV等价于worst-case VaR组合，并且其风险厌恶系数等效于具体的$\varepsilon$。

- 论述：
- 通过收缩估计的思想，$ \kappa $调整等同于将期望收益向均值（$v \mathbf{e}$）收缩，提供了稳健优化的三种统一视角。

3. 分散悖论与稀疏性分析

• 问题聚焦：

- 是否不确定性越大必然导致更分散投资？作者反驳，表明在某些参数区间内，增加不确定性可能导致减少资产数量；

• 数学建模：

- 通过参数化协方差矩阵$\Sigma(\sigma,\rho)$，并假设交易成本为固定值$\phi e$，导出资产数量$s$优化问题简化为单变量形式，分析解空间；

• 命题4（资产数量变化条件）：

- 根据不确定性参数微小增量$\Delta$，资产数量$s$可能减少、持平或增加，具体条件取决于关于交易成本、收益结构的边界函数$B{-}(s^)$和$B{+}(s^)$。

• 图表内容：

- 图2（可视化三种条件区域：C1减少，C2持平，C3增加）明确展示不同参数组合对组合稀疏性的影响域。

4. 计算算法设计

• 模型性质：

- RSMV模型属于NP难度的混合整数二次规划问题；
- 引入连续非凸的差分凸（Difference-of-Convex，DC）近似处理非连续指示函数$\mathbb{1}(\mathbf{x})$，采用带有截断的$capped-\ell1$函数逼近，实现稀疏优化。

• 提出算法：

- SN-pDCA：基于近端差分凸算法，迭代中使用半光滑牛顿法精确求解子问题，提高求解速度；
- 算法设计依据：
- 使用截断$capped-\ell1$函数替代0-1指标函数，兼顾偏倚校正和稀疏性；
- 证明其局部线性收敛性，保证收敛鲁棒性；
- 对应理论——利用Kurdyka-Łojasiewicz (KL)性质及相关凸分析技巧。

• 算法步骤：

- Algorithm 1 — 近端DC迭代步骤（生成一序列提升的二阶信息，求解凸子问题，线搜索更新）；
- Algorithm 2 — SN-pDCA，将半光滑牛顿-共轭梯度解决子问题整合入Algorithm 1，保障超线性收敛。

5. 数值实验与性能验证

• 数据集：

- 多组不同规模的数据集，包括Fama-French行业组合（12-100只股票）、标普500成分股（326只）、罗素2000指数子集（500-1074）；
- 涵盖日频和月频收益率，贴近现实应用。

• 比较基准：

- CPLEX（精确解求解器，受限于计算资源和求解时间，适用于小中型问题）；
- L1MV模型（标准凸$\ell1$正则化组合优化，用于比较稀疏效应和算法效率）。

• 关键发现：

- SN-pDCA提供的解质量较CPLEX接近（误差小于10%），明显优于L1MV的误差，且SN-pDCA获得的非零资产数通常更少，体现更强稀疏性；
- SN-pDCA在计算时间上远快于CPLEX，尤其在资产数量大于100时；
- 利用L1MV解降低问题维度后，加速版本（Ac-SN-pDCA）更进一步提高效率；
- 从热力图（图4）和数值表（表3）反映出SN-pDCA算法的强大实用性与准确度。

• 稀疏性-不确定性关系实证：

- 不同参数$\epsilon$和固定交易成本条件下，组合肩书基数曲线表现为先降后升或持平，符合理论预测的“多元分散悖论”；
- 通过图5展示FF17、FF30、SPX326等多数据集下的这种稀疏性随参数变化趋势，具有良好泛化性。

6. 结论部分总结

• 报告提出基于稳健与稀疏双重考虑的投资组合优化新模型，有理论深度及实际应用价值；

- 算法创新融合了差分凸优化与半光滑牛顿技术，有效解决大规模组合稀疏优化难题；

• 理论与数值结合，清晰揭示了风险厌恶系数与模型参数不确定性之间的双向联系，并从多角度诠释了分散悖论的实质；

- 结果对投资组合管理实践和学术研究均具有指导及借鉴意义。

---

三、图表深度解读

图1：MV与RMV效率前沿

• 图示红色为经典MV效率前沿，蓝色、黄色、青色分别对应不同$\varepsilon$参数设定下的RMV效率前沿；

- 观察发现，RMV效率前沿是MV效率前沿的子集，且随着不确定性增加，前沿面积缩小，投资者更趋向于选择最低波动策略；

• 该图直观支持命题1中凸组合权重随着$\varepsilon$变化动态调整的结论[page::8]

图2：资产数量变化的可行区域

• 将不确定性变化$\Delta$和交易成本$\phi$绘制二维平面，划分出三大区域条件C1（减少资产数量）、C2（资产数保持）、C3（资产数增加）；

- 该图反映资产数量决策受复杂因素驱动，揭示“分散悖论”背后种种可能；

• 投资者在不同参数环境中调整组合规模权衡风险与成本[page::12]

图3：指标函数与$\ell1$及截断$\ell1$函数对比示意

• 一维函数图展现指标函数的跳跃性，简单$\ell1$罚项的线性增长与截断$\ell1$（capped-$\ell1$）的平坦段特性；

- 表明截断$\ell1$更加接近0-1指标函数，有利于优化过程中减少估计偏差并增强稀疏性；

• 这种函数形式为后文差分凸分解与算法设计的数学基础[page::14]

图4：不同算法求解结果热力图（FFInd12及FFInd17数据）

• 行为资产编号，列为不同算法（CPLEX原始解，SN-pDCA，L1MV）；

- 单元格色深表示资产权重的大小，右侧标注配色映射；

• SN-pDCA权重分布更接近精确CPLEX解且显著较L1MV解更稀疏(零元素更多)，体现算法优势[page::22]

表3：算法比较的结构化数值结果

• 对不同数据集，分别记录目标函数值、组合非零元素个数（即稀疏性指标）、算法运算时间；

- CPLEX计算时间随资产数量扩增严重膨胀，许多高维问题达最大计算时间限制（600秒）；

• SN-pDCA及Ac-SN-pDCA在求解时间和结果精度均优于L1MV，Ac-SN-pDCA对大规模数据表现尤为显著[page::21]

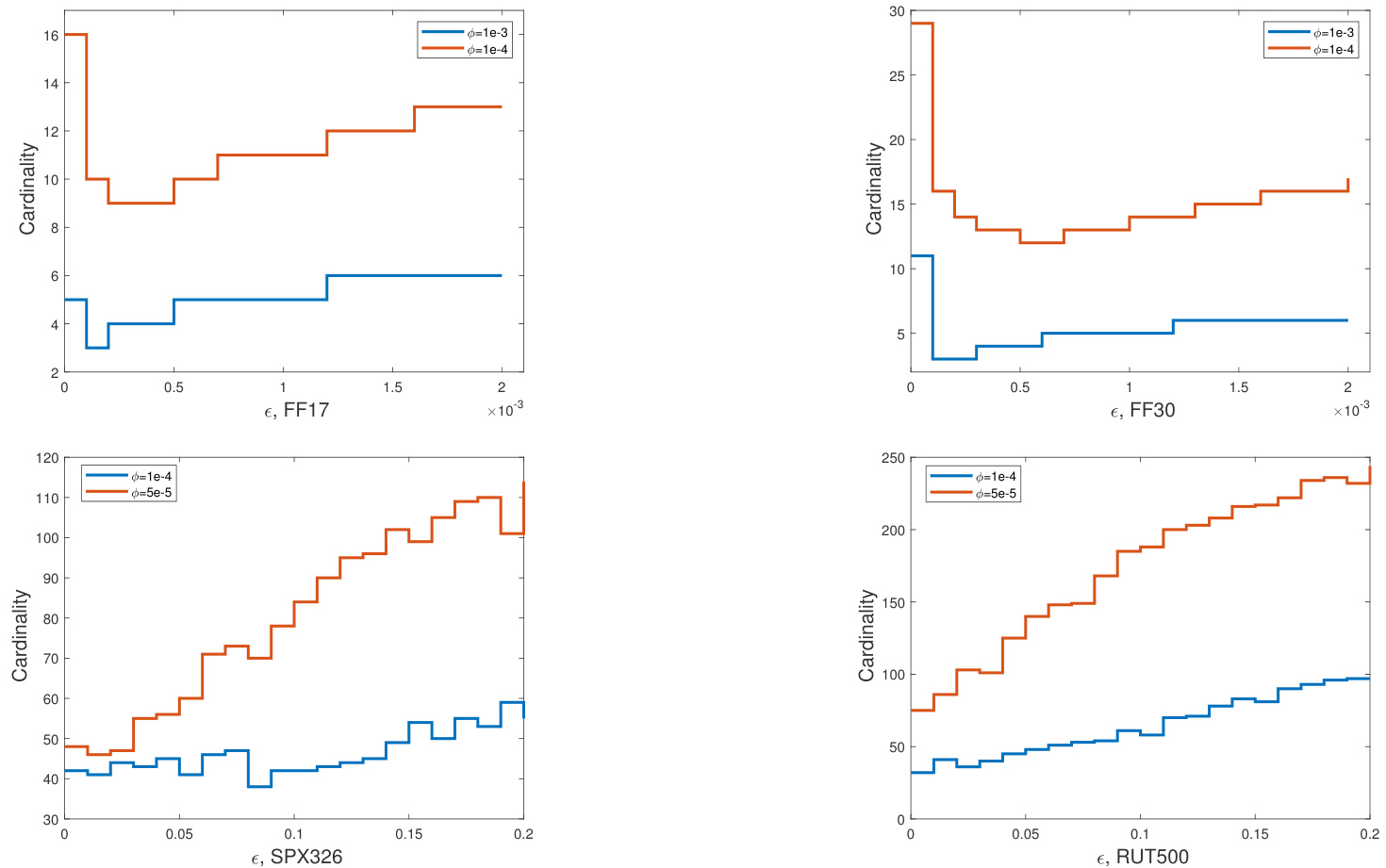
图5：稀疏性随不确定性$\epsilon$变化关系图

• 四个子图对应不同数据集，横轴为$\epsilon$，纵轴为投资组合非零元素个数；

- 在固定交易成本$\phi$下，资产数量呈现先降低后缓慢上升或持平趋势，符合理论对“分散悖论”的描述和分析；

• 数值结果验证理论的普适性，说明稳健与稀疏约束对组合选择结构影响深远[page::24]

---

四、估值分析

该报告聚焦组合优化算法与稳健稀疏模型，并未涉及传统意义上的“估值”过程（如股票内在价值评估、企业估值模型等）。估值部分聚焦投资组合风险-收益权衡，通过定义风险厌恶系数$\kappa$及不确定集$\varepsilon$参数调节组合权重的分散性。报告核心在于模型构造与算法求解的数学优化范畴。采用的优化目标函数包含：

• 组合方差（$\mathbf{x}^T \Sigma \mathbf{x}$），风险度量；

- 收益期望不确定性的稳健补偿项（如椭球不确定集引入的WVaR）；

• 稀疏性惩罚（固定交易成本$ \phi^T \mathbb{1}(\mathbf{x}) $）。

---

五、风险因素评估

报告着重解决由于估计误差导致的组合优化不稳定性风险，采用稳健优化减弱参数不确定对结果的负面影响，详见以下风险要点：

• 参数不确定风险：均值和协方差矩阵的估计误差会剧烈影响MV组合权重，报告通过椭球不确定集显式建模该风险，降低样本外组合表现波动；

- 过度分散风险：含有交易成本时，过多小额头寸可能存在不经济性，固定交易成本策略避免这一风险；

• 计算风险：混合整数优化问题存在计算复杂度瓶颈，通过提出高效SN-pDCA算法，实现大规模问题求解，提高模型适用性和稳定性；

- 模型假设风险：协方差矩阵假设已知固定，实际可能存在模型设定误差，报告虽未详细探讨该风险，但已通过理想化假设简化模型结构。

---

六、批判性视角与细微差别

• 报告使用的假设较多，尤其是椭球不确定集、均值估计误差主导风险及固定费用固定，这些可能在现实投资中变动较大；

- $\kappa$与$\varepsilon$的一一对应关系虽理论证明，但实际中投资者对风险厌恶参数的主观确定仍复杂，如何精准匹配是应用难点；

• $\ell2$范数替代以及截断$\ell1$近似虽然具有理论支持，但在极端市场条件或不连续风险事件下的稳健性仍需进一步验证；

- 算法性能依赖于参数选择（如截断参数$t$、步长控制），实际运行时可能需细致调参，且加速版本虽效果优越，但理论支持尚不完备；

• 投资组合限制设置较少（如无多期动态限制、无更多市场约束），拓展时需注意模型和算法通用性。

---

七、结论性综合

综合来看，报告成功构建了扩展经典MV框架的稳健稀疏投资组合模型（RSMV），并通过以下方式做出贡献：

• 模型创新：

- 结合资产收益期望的不确定性（利用椭球不确定集体现发散性）和固定交易成本推动组合权重的稀疏性限制；
- 从理论证明风险厌恶系数与稳健参数之间的交互机制，统一多种稳健方法视角；
- 深刻揭示并数学特征化“分散悖论”：参数不确定性并非总促使组合分散，部分情况下实际可能走向更集中。

• 算法突破：

- 设计并规范了以半光滑牛顿法为基础的近端差分凸算法（SN-pDCA），实现了高效、大规模求解能力，区分局部与全局收敛结果；
- 采用非凸截断$\ell1$函数修正标准$\ell1$的偏差，兼顾稀疏性和估计性能；
- 数值实验表明SN-pDCA在多个资产规模和实际数据集上均优于灵敏度较高的CPLEX和传统$\ell1$模型。

• 图表深刻洞察：

- 效率前沿图证实RSMV模型的稳健版本是经典MV组合风险-收益空间的子集调节；
- 资产选择数量图揭示参数不确定与交易成本双重作用下的“分散悖论”不同区域，辅助投资者调节组合规模；
- 热力图与稀疏性曲线直观反映实际数据中稳健稀疏模型的组合结构变化与算法表现。

• 总体判断：

- 报告呈现了一套理论与实践兼备的稳健稀疏投资组合系统，提供了优于传统MV组合的风险管理工具及算法技术支持；
- 其数学严谨性和计算效率均为该领域重要进展，值得学界及实务界关注与推广。

---

附录：报告中部分重要图表

图1：MV和RMV效率前沿


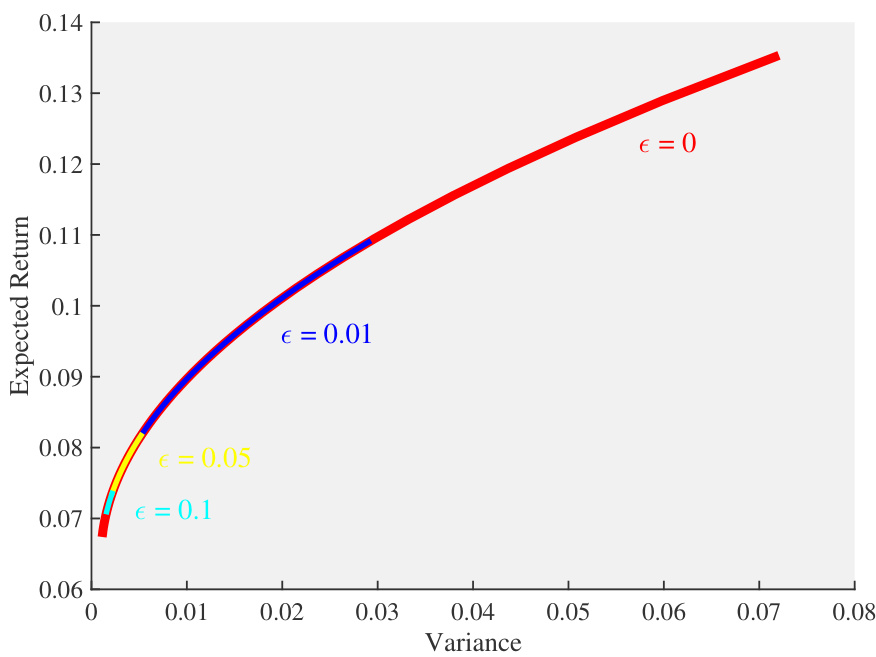
图2：不确定性与交易成本下资产数量变化可行区间


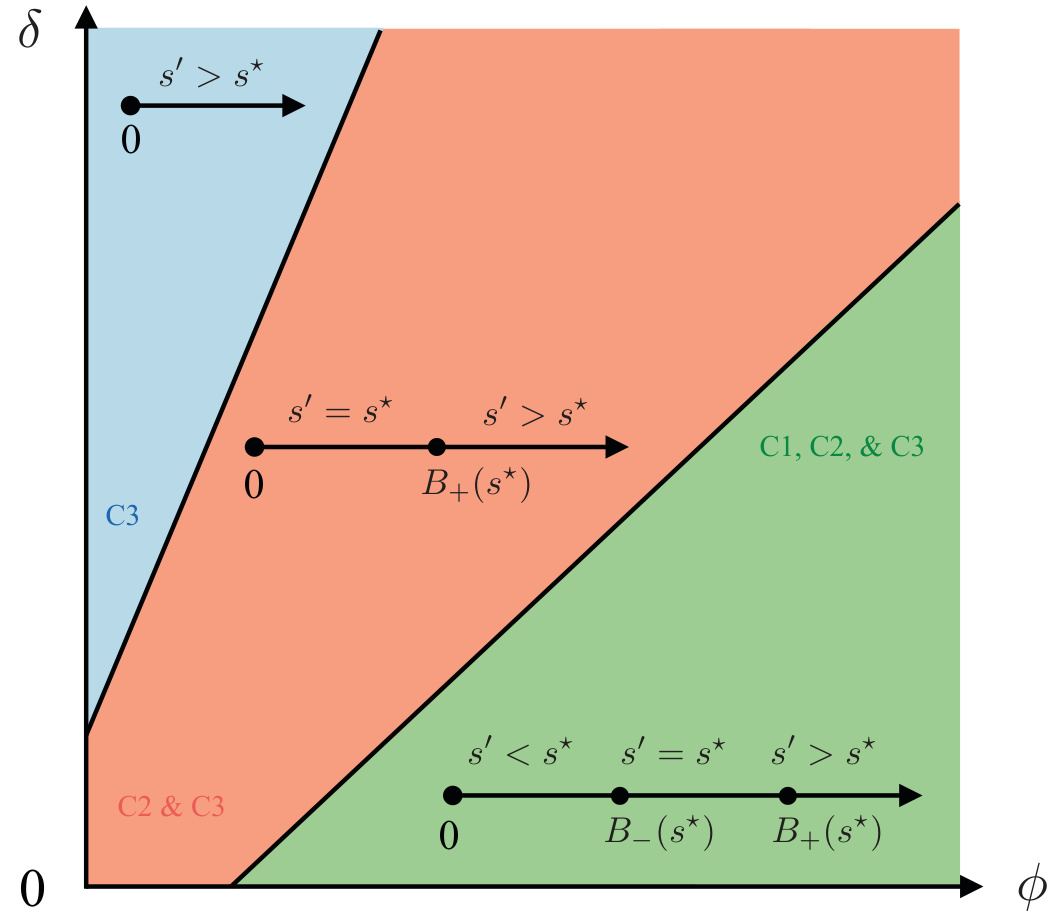
图3：指标函数与截断$\ell1$函数对比


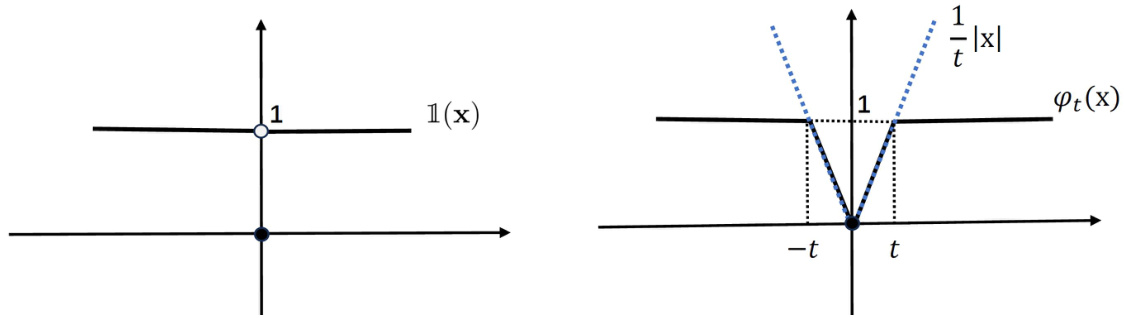
图4：算法求解结果权重热力图（FFInd12与FFInd17）


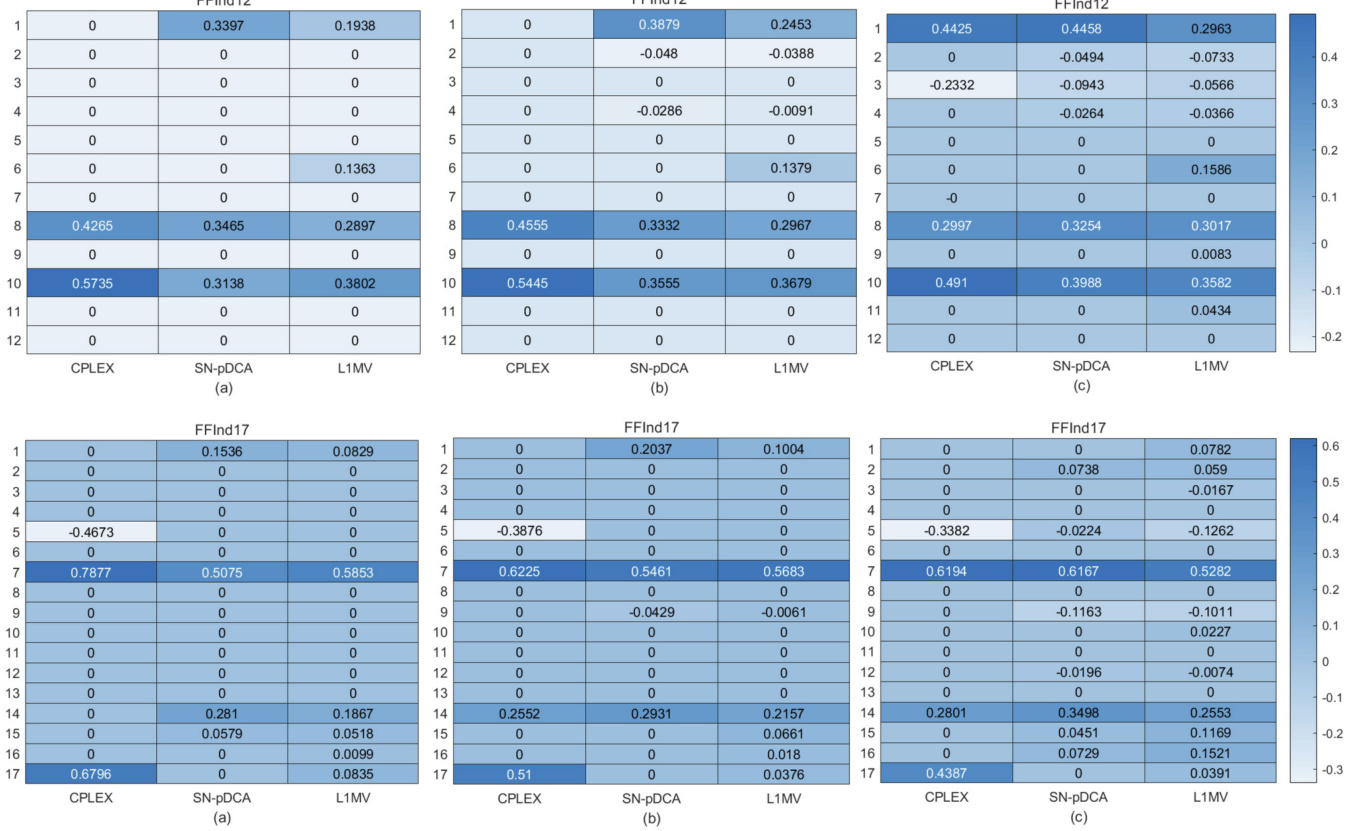
图5：不同数据集RSMV组合稀疏性与不确定性关系


---

结尾备注

本分析严格依据报告内容与页码逐条展开，务求详尽客观、涵盖模型假设、理论证明、算法设计与数值实证等所有关键内容，力图为金融工程与量化投资研究者提供精确且深入的技术解读与参考。[page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]

报告