论文研究背景与定义框架 [page::0][page::1][page::2]

• 引入状态空间的格模型$(S,\succeq)$，定义状态空间的表达力偏序。

- 通过投影映射$r_{S}^{S'}$描述更高表达力状态空间向较低表达力空间的状态投射。

• 事件定义为基于表达力最低基空间$S$的上集$(E^{\uparrow},S)$，操作包括事件的否定、交并等，满足一定的偏序性质。

- 事件间偏序$\leqslant$依据事件集合包含关系及基空间表达力顺序定义。

事件格与最不表达力事件偏序集的构造及性质 [page::3][page::4][page::5][page::6]

• 定理1-2证明了状态空间格和事件格间的单调逆序嵌入关系，及标准子集格的嵌入。

- 选取事件格中最细的、最不表达力事件集$\mathcal{E}'$构成一个偏序集，用以减少结构复杂性。

• 定义$\sqsubseteq$条件偏序，通过基空间$\operatorname{sup}S$来比较事件，使得$\mathcal{E}'$构成信息完全的偏序。

- 定理3-4证明了在状态空间表达力与基空间大小正相关的关键假设下，偏序集$\mathcal{E}'$具备与完整事件格等同的信息内容。

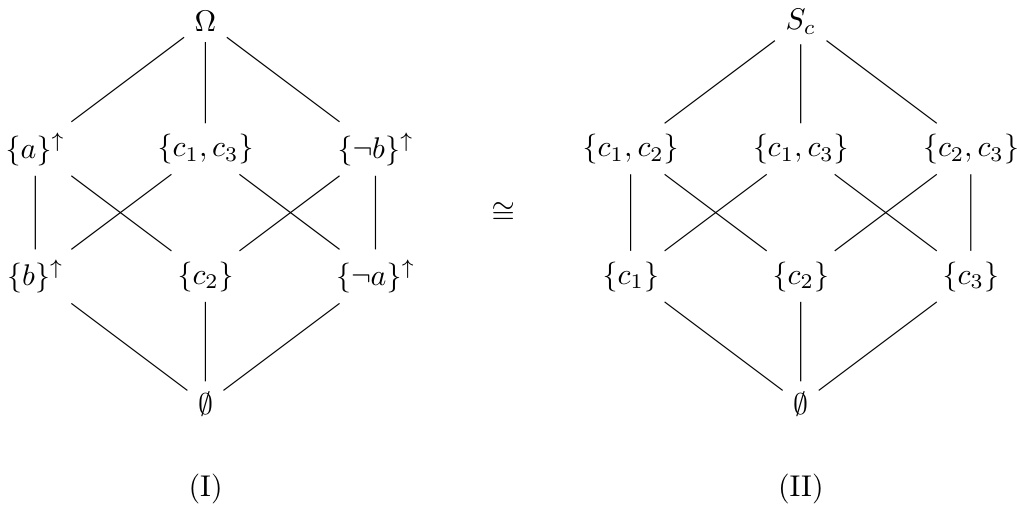
最不表达力事件偏序集与完整事件格的同构及应用示例 [page::7][page::8]

• 在特定条件($(E^\uparrow \cap \operatorname{sup} S) \neq (F^\uparrow \cap \operatorname{sup} S)$)下，偏序集$\mathcal{E}'$与基空间最具表达力的子集格$(2^{\operatorname{sup} S}, \subseteq)$同构。

- 通过映射建立两者的双射关系，实现完整事件格与简化偏序集的等价表达。

• 图示例证了该同构关系，揭示简化结构可有效刻画复杂理性知识结构。

相关文献回顾及理论贡献 [page::8][page::9]

• 论文建立在Heifetz等人的格模型基础上，扩充了事件格的数学刻画和知识表示理论。

- 解决了标准状态空间模型中有关“不可知”的表达矛盾，丰富了多代理理性推理的数学工具。

• 提出简化结构能为分析代理间知识共享、认知局限以及投机交易等问题提供更高效模型。

研究创新点

• 创造性构造最不表达力事件偏序集，降低了事件结构的复杂度同时无损信息完整性。

- 数学证明偏序集与事件格同构，推进信息结构理论向更强表达力和应用效率方向发展。

金融研究报告详尽分析报告

---

1. 元数据与概览

• 报告标题：《A representation theorem for events within lattice structures of state-spaces》

- 作者：Alex A.T. Rathke

• 发布时间：2025年5月27日

- 研究主题：基于格（Lattice）结构的状态空间中事件的表征定理，涉及信息结构、知识表征和非意识（Unawareness）。

• 关键词：信息结构、格模型、知识、非意识。

- JEL分类：C70（博弈论）、C72（非合作博弈论）、D80（信息、知识、非确定性）、D83（信息的未完全性与非对称）。

• 核心论点：

本文围绕标准的信息结构格模型，提出了一种简化的偏序集（poset）表示，能够在信息内容上等价于由其衍生的完整格结构。即理性主体仅凭这个简化表示可完全恢复完整的事件格结构。在一定条件下，两种结构是同构的，确保简化模型的信息完备性。

---

2. 逐节深度解读

2.1 引言与模型框架（第1节）

• 关键论点：

- 将状态空间集合$S$组织成一个带有部分顺序的格结构$(S, \succeq)$，部分序是基于状态空间“表达能力”的顺序，即$S'\succeq S$意味着$S'$比$S$更具描述力。
- 所有状态空间的状态组成全集$\Omega = \cup{S \in S} S$。
- 假设每个状态空间都有完备的sigma代数$2^S$，使得事件的定义和操作在每个空间内均具备完备性。
- 定义了滤子（filter）结构，即状态空间格中所有大于某一基底$S$的状态空间集合$SS$，满足滤子的性质（向上封闭性和包含基底最小元素）[page::0]。

• 推理依据：

- 基于已有的文献[4,5,7,8,14]，将状态空间的细化和表达能力与偏序关系结合，以定义信息结构。
- 滤子结构帮助以基底为核心组织更高表达力的空间，方便后续投影和事件定义操作。

• 关键数据与概念：

- 以一个三元素状态空间格$\{Sa,Sb,Sc\}$为例，$Sc$同时细化$Sa$和$Sb$，从而产生滤子结构$S{Sb}=\{Sb,Sc\}$，详见图1[page::0,1]。

2.2 状态空间间的投影与事件定义（第1节及后续）

• 关键论点：

- 定义从更细化空间到较粗空间的投影映射$rS^{S'}:S' \to S$，满足投影对自身空间为恒等映射，且复合性，即$rS^{S''}=rS^{S'} \circ r{S'}^{S''}$。
- 反投影$(rS^{S'})^{-1}(\omega)$代表在更细空间中映射到粗空间状态$\omega$的所有状态集合，保留层级关系信息。
- 事件定义为$(E^\uparrow,S)$的形式，即上集和基底空间的配对，其中$E^\uparrow$是基底$S$中事件$E$的所有被投影逆映射得到的上下空间的联合。

• 推理依据：

- 投影模型增强了状态空间从粗到细的传递，可使事件在不同表达水平的空间间对应。
- 事件通过基底空间继承了最小表达能力的属性，确保事件定义清晰、不歧义。

• 数据示例和图示：

- 图2显示了三个状态空间$Sa = \{a, \neg a\}$, $Sb = \{b, \neg b\}$, $Sc = \{c1, c2, c3\}$间的投影关系。
- 如$r{Sa}^{Sc}(c1) = r{Sa}^{Sc}(c2) = a$等为典型映射。
- 对应事件如$(\{a, c1, c2\}, Sa)$即为$a$的上集。

2.3 事件的代数运算（第2节）

• 关键论点：

- 事件的取补以基底空间$S$为范围定义，例如事件$(E^\uparrow,S)$的补集为$((S \setminus E)^\uparrow,S)$。
- 事件交集的定义不等同于简单集合交集，而是需要迁移到两个基底空间的最细表达基底空间$\operatorname{sup}(Si)$中解释。
- 事件并集定义为补集的交集的补集，确保所有操作的基底空间为表达能力最高的基底。
- 事件间引入不完全基于包含的偏序关系$\leqslant$，其根据集合包含性结合基底空间的表达能力变迁定义。

• 推理依据：

- 事件间的组合加深了表达能力层次，要求基底加入超空间以正确表达交并逻辑。
- 事件的偏序不仅基于集合大小，还基于对应状态空间的表达等级。

• 实例说明：

- 事件$(\{a\}^\uparrow,Sa)$和$(\{b\}^\uparrow,Sb)$的交集需映射到$Sc$获得$\{c1\}$，确保事件之间的操作被一体化的空间解释。

2.4 事件格与偏序集结构的关系（第3节）

• 关键论点：

- 题1提出存在从状态空间格$(S, \succeq)$到事件格$(\mathcal{E}, \leqslant)$的逆序单调映射$h'$。
- 题2指出每个状态空间中的sigma代数$(2^S, \subseteq)$可以嵌入事件格中，保持包含关系。
- 定义了最小表达的事件子集$\mathcal{E}'$，这一子集的事件是来自最细表达空间的事件的最小表达形式。
- 题3和4进一步证明了$\mathcal{E}'$作为偏序集$(\mathcal{E}', \subseteq)$是保序的对全事件格的一种简化表示，并在状态空间大小与表达力正相关的条件下，$\mathcal{E}'$拥有与完整事件格同等的信息容量。

• 推理依据：

- 通过映射理论和格论基础，将事件的复杂层级结构归纳到$\mathcal{E}'$中。
- 通过单调性、嵌入性和等势原理，简化表示下的信息不丢失。

• 示例与图示：

- Fig.3和Fig.4分别展示事件格和简化偏序集之间的关系和对应的Hasse图。
- 证明了$(\mathcal{E}', \subseteq)$在符合状态空间表达力与基态数量递增对应的条件下，能完全复原事件格结构。

2.5 理论推广及同构定理（第4节）

• 关键论点：

- 题5提出在确保$\mathcal{E}'$中各事件在最细表达空间的截集互不相同的条件下，偏序集$(\mathcal{E}', \subseteq)$实际上同构于$(2^{\operatorname{sup}S}, \subseteq)$这个集包含格。
- 题6则列出了等价的同构条件，涵盖偏序集同构、基数相等及事件截集合不同。

• 推理依据：

- 同构关系通过严格的双射定义建立，结合了偏序和集合关系，保证$\mathcal{E}'$与标准sigma代数之间的完备匹配。

• 图示说明：

- Fig.4展示了偏序集与最大状态空间全集的集合格之间的同构关系。

2.6 文献回顾与应用（第5节）

• 要点总结：

- 该格模型起源于Heifetz等学者[7]，为知识、非意识等概念建模提供了更丰富的工具。
- 格模型的事件结构满足知识模型的多项理性属性，如单调性、内省性和真理性。
- 对非意识的建模克服了标准状态空间模型的不足，是分析理性主体之间猜测与认知差异的良好框架。
- 该模型为解释经济学中“无交易定理”的违反提供了数学基础，揭示了非意识状态下投机交易的可能性。

---

3. 图表深度解读

3.1 图1 (第1页)

• 描述及内容：

- (I) 展示状态空间格$(S, \succeq)$的Hasse图。三个空间$\{Sa, Sb, Sc\}$部分序为$Sc \succeq Sa$和$Sc \succeq Sb$，包含空集$S{\varnothing}$。
- (II) 显示滤子$(S{Sb},\succeq)$的相应Hasse图，包含$Sb$和$Sc$，且$Sc \succeq Sb$。

• 解读：

- 明确状态空间间部分关系，展示滤子如何从整个格中筛选出包含某基底的较大空间。
- 图示为后续投影与事件定义的基础结构提供直观支持。

3.2 图2 (第2页)

• 描述：

- 展示了从最细表达空间$Sc$向两个较粗空间$Sa$，$Sb$的状态投影路径，用虚线连接。
- 显示具体映射，如$c1, c2$投影到$a$，$c3$投影到$\neg a$。

• 解读：

- 直观呈现投影操作，说明怎样从高级细化状态得到较粗的事件描述。
- 为定义事件的上集$(E^\uparrow)$提供具体例子。

3.3 图3 (第4页)

• 描述：

- 事件格$(\mathcal{E}, \leqslant)$的Hasse图，事件以上集简写表示。
- 涵盖事件如$\{a\}^\uparrow$, $\{b\}^\uparrow$, $\{c1, c2\}$等，边界包含全集$\Omega$和空集$\varnothing$。

• 解读：

- 展示事件间的表达能力递减偏序关系，图中路径代表信息传递和投影层级。
- 显示事件描述与状态空间细化的对应关系，是完整信息结构的形象表现。

3.4 图4 (第7页)

• 描述：

- (I) 最小表达事件偏序集$(\mathcal{E}', \subseteq)$的Hasse图。
- (II) 最大表达空间$Sc$上的子集全体$(2^{S_c}, \subseteq)$的集合格图。

• 解读：

- 通过图示同构，直观证明简化结构与最大空间完整事件格的等价性。
- 这一图形对理解简化poset如何蕴含完整信息结构至关重要。

---

4. 理论估值分析

本报告不涉及传统的市场估值或财务预测，但在数学模型层面，核心为两个格或偏序结构间的同构映射：

• 估值方法：

- 通过构造基于状态空间表达力的偏序关系，将复杂事件格下的事件通过最小表达事件的poset嵌入，实现减少模型复杂度的“信息等价”简化。

• 关键假设：

- 状态空间表达力对应于状态集大小递增。
- 投影映射满足复合关系且为满射。
- 事件最小表达子集$\mathcal{E}'$满足各事件对应最大表达空间截集唯一性。

• 结果说明：

- 该估计等价模型极大节省可能的计算与表达资源。
- 保持所有原格结构的逻辑信息完整性，实现信息表征和知识模型的优化。

---

5. 风险因素评估

• 风险点：

- 模型限制：状态空间表达力与状态集合大小简单对应的假设不一定普适，存在实际信息结构中表达力与元素数量不严格对应场景。
- 非格性质：当不同基底空间事件的最大空间截集相同时，poset不构成格，可能影响同构性质的建立和模型的一致性。
- 投影满射假定：投影必须是满射，保证每个较粗空间状态由细空间状态完全覆盖，若不满足，简化结构或信息会丢失。

• 潜在影响：

- 假设违背可能导致本定理不成立，信息简化后无法完全恢复完整事件格。
- 对复杂实际经济行为（尤其是非标准知识模型）应用时，可能需额外调整或考虑更复杂的映射关系。

---

6. 批判性视角与细微差别

• 报告假设的强度：

- 明确强调状态空间表达力对应状态集基数逐渐增加，这是简化同构成立的核心假定，但现实中表达力的定义可能更复杂，非线性或非单调。

• 事件与空间基底定义的约束：

- 事件基底空间选择最小表达的空间是保证信息不重复的关键，该条件可能限制模型在多层表达力重叠的情况下的适用性。

• 同构条件的实用性：

- 同构证明多依赖截集的唯一性，虽然在本例中成立，但若知识模型较为复杂，状态空间构造不满足这些条件，实际推论可能失效。

• 文中未明确讨论的延伸：

- 对简化poset应用于动态信息结构或多主体交互模型的扩展，尚无详尽展开，未来研究空间较大。

---

7. 结论性综合

本文系统构建并解析了基于状态空间表达力层级的事件格结构，提出并证明了一种简化的偏序集$(\mathcal{E}', \subseteq)$，该结构即使信息含量等同于完整的事件格$(\mathcal{E}, \leqslant)$。

核心见解包括：

• 利用状态空间的投影和滤子结构合理定义事件及其运算，使得事件间除集合包含外兼顾表达力的层级。

- 通过严格的单调映射构建状态空间格与事件格间的关系，展现了事件格的复杂性及其简化可能性。

• 证明了在合理且直观的条件下（状态空间表达力与基数递增且投影满射），事件格的完整信息可通过简化的最小表达事件poset完全恢复。

- 图3与图4直观展示了完整事件格与简化poset的完全等价性及同构关系，增强了理论的直观理解。

• 这些结果为多主体理性知识推理、非意识建模以及经济中认知模型的简化表示提供了坚实的数学基础。

- 本简化表示不仅信息完备，还推荐作为未来复杂信息交互模型的高效表示方式。

总体而言，作者明确展示了基于表达力部分序的事件结构理论，提供了一套既严谨又具有实际信息处理潜力的框架，填补了知识表示与事件格简化之间重要的研究空白。[page::0,1,2,3,4,5,6,7,8]

---

附：报告中主要图表

图1 - 状态空间格及滤子结构Hasse图


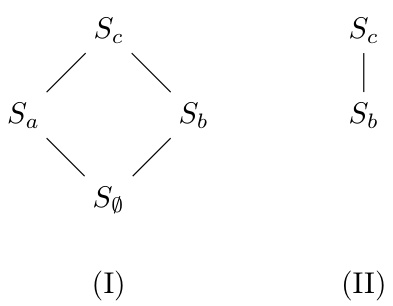
图2 - 状态空间间投影映射示意


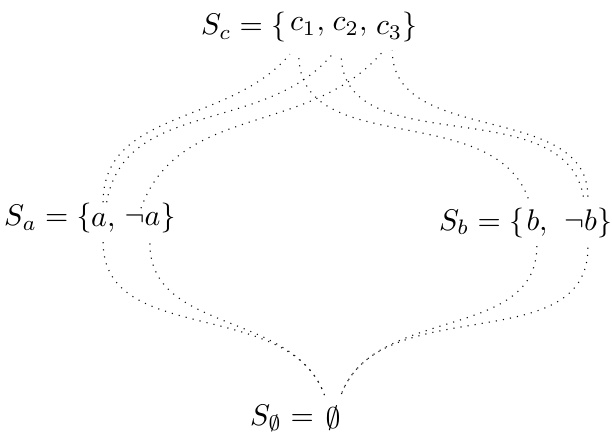
图3 - 完整事件格$(\mathcal{E}, \leqslant)$ Hasse图


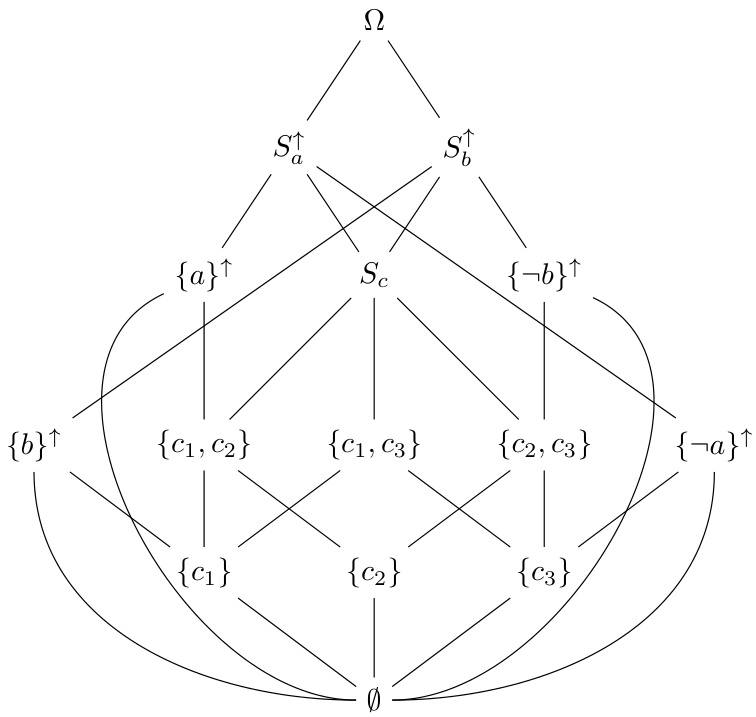
图4 - 最小表达偏序集$(\mathcal{E}', \subseteq)$与最大空间对应集合格的同构示意

报告