• 本文研究了面对多重损失模型不确定性的保险公司如何设计最优风险分担合同，纳入了多个参考概率模型及卡方散度惩罚，以单调均值-方差（MMV）偏好为准则，解决了时间一致性问题 [page::0][page::1][page::5].

- 定义了辅助过程$Z{k,t}$为每个参考模型到优化模型$\mathbb{Q}^$的Radon-Nikodym导数过程，显示最优财富过程$Xt^$为$Z{k,t}$的线性组合，具有解析表达式 [page::6][page::11].

• 证明最优赔付策略$\alpha^(t,\xi,z)$和对手方风险调整率$\beta^(\xi)$具有显式反馈形式，其中策略为基于风险溢价和模型分布加权的调整，体现为损失函数的广义超额损失再保险形态 [page::7][page::10].

- 计算证明财富过程$Xt^$在最优测度下期望等于无风险分担基准过程期望，且方差受到模型惩罚参数$\theta$的平方反比控制，$\theta$越大，财富波动越小 [page::13][page::14][page::15].

• 验证了策略和价值函数的可行性及最优性，满足哈密顿-雅可比-贝尔曼-伊萨克斯（HJBI）方程及相关边界条件 [page::15][page::16][page::17][page::18][page::20].

- 单模型情况下，最优策略简化为固定阈值再保险合同，辅助过程和财富过程均可表达为Poisson过程函数，辅助过程与财富过程承担完美负相关 [page::21][page::22].

• 对手方根据固定安全负载率$\eta$最大化自身期望财富，明确计算了期望表达式，证明单模型下最优安全负载存在且唯一，给出了通过Lambert W函数计算最佳$\eta^$的解析解 [page::23][page::25].

- 基于西班牙汽车保险数据，使用交叉验证估计100个参考模型和对手方模型，验证参数满足技术假设，模拟显示随着$\theta$的增大，财富分布方差明显下降，风险分担策略效果显著[page::26][page::27]:

• 模拟多个辅助过程$Z_k^$路径展示了其对财富过程$X^$的负线性关系，表明模型距离与财富行为的关系 [page::27]:

• 对手方风险定价问题数值解示范了安全负载$\eta^*$与惩罚参数$\theta$的正相关性，表明风险约束更严苛时，对手方收取更高的安全负载 [page::28][page::29]:

金融研究报告详尽分析报告

---

1. 元数据与概览

• 报告标题：Model Ambiguity in Risk Sharing with Monotone Mean-Variance

- 作者：Emma Kroell, Sebastian Jaimungal, Silvana M. Pesenti

• 所属机构：多伦多大学统计科学系

- 发布日期：2025年4月7日

• 研究主题：探讨在多模型不确定性下，应用单调均值-方差（Monotone Mean-Variance, MMV）偏好对保险公司风险分担及其优化策略的影响，特别关注含模型多样性和不确定性的风险分担及优化问题。

核心论点与主要信息

本研究针对保险公司在面对不确定的保险赔付（损失）风险时，如何在存在多个竞争模型且对真实模型存在模糊性的情形下，设计最优风险分摊合同。作者基于Maccheroni等人提出的单调均值-方差偏好，引入了考虑多模型的模型不确定性惩罚，并应用Cramér-Lundberg跳跃损失模型，全面推导出最优风险分摊策略及其财富过程的半解析表达式。此外，报告还讨论了对手方（风险分散方）如何确定最优的合同价格，并结合西班牙汽车保险数据进行实证与数值验证，展示了理论结果的实用性与有效性。[page::0,1]

---

2. 逐节深度解读

2.1 引言（Introduction）

• 关键论点：实际保险与金融领域中，决策方常面临多重备选模型，每个模型依据不同的数据源或专家意见而来，且可能无法确定哪个模型为“真实”。例如，气候变化导致历史赔付数据难以预测未来风险，需引入包含极端风险的多种模型。

- 方法创新：针对这种多模型模糊，作者提出将多模型融入统一的惩罚框架，求解策略以应对模型不确定性。该方法区别于传统单一模型鲁棒优化，通过chi-squared散度（而非更常用的Kullback-Leibler散度）实现模型不确定性惩罚。

• 理论基础：借鉴Maccheroni等提出的单调均值-方差偏好（MMV），提供与经典均值-方差的单调性强化版本，提升时间一致性。报告提出如何将MMV扩展至含多模型的设置，解决不一致性和最优策略问题。[page::0,1,2]

2.2 问题设定（Problem Setting）

• 模型结构：

- 损失通过带补偿的Poisson随机测度（Poisson Random Measure, PRM）驱动，保险公司和对手方各自拥有不同的损失强度与分布（补偿密度）$vk(\xi)$。
- 保险公司财富以Cramér-Lundberg模型表述，包含固定保费收入与随机赔付出险。
- 保险公司可通过风险分摊函数$\alphat(\xi)$与对手方分摊部分赔付，对手方按自身模型收取带安全加载（markup）的保费。

• 技术假设：

- 假设赔付分布在不同模型间满足积分条件（Assumption 2.1, 2.2），限制模型差别不至过大。
- 给定风险分摊策略的可接受性条件（定义2.3），确保策略满足二阶矩条件方便数学分析。

• 目标函数与偏好：

- 保险公司基于多模型下的单调均值-方差偏好，定义形式为在所有候选概率测度间以chi-squared分歧作为不确定性惩罚。
- 明确惩罚权重$\pik$分配不同模型贡献，罚项为加权chi-squared散度期望。
- 此类准则保障时间一致性，解决了传统均值-方差偏好在动态情景下的缺陷。
- 通过辅助过程（Radon-Nikodym导数进程）的引入，转换为随机控制问题便于求解。

• 贡献点：

- 给出最优风险分摊策略与财富过程的半显式表达，证明策略的适定性与验证定理。
- 分析对手方如何设定安全加载率，反映合同定价机制。
- 以西班牙汽车保险数据为例，展示模型估计、风险分摊策略效果及对手方价格选择。[page::3,4,5,6]

3. 保险公司的最优风险分摊策略（Insurer’s optimal risk sharing strategy）

• 优化问题：

- 保险公司最大化互优化准则，涉及对策略$\alpha$的最大化及对候选测度对应的补偿函数$\beta$的最小化。
- 价值函数定义为在最优控制下，保险终端财富加上惩罚项的期望。

• 主要数学工具：

- 采用Hamilton-Jacobi-Bellman-Isaacs (HJBI)方程框架，建立对应的微分方程。
- 通过变分法确定最优策略与补偿函数的闭式表达。
- 策略$\alpha^$形如“$\xi$ 减去一个带权重的损失调整项”，做为风险保留限额的推广；补偿函数$\beta^$为对手方模型补偿的一个放大版本，比例由安全加载$\eta$控制。

• 关键结果（Proposition 3.2）：

\[
\alpha^{}(t,\xi,z) = \xi - \frac{1}{\theta} \sum{k\in \mathcal{T}} \pik zk \ellk(T - t) \left[(1+\eta) \frac{vC(\xi)}{vk(\xi)} - 1\right]
\]
\[
\beta^{}(\xi) = (1 + \eta) vC(\xi)
\]
\[
\ellk(t) = \exp\left( t \int{\mathbb{R}+} \left[1 - (1+\eta) \frac{vC(\xi)}{vk(\xi)} \right]^2 \nuk(d\xi) \right)
\]

• 策略解读：

最优策略表现为对赔付$\xi$的减法调整，调整项依赖于各模型权重、辅助过程$zk$和安全加载$\eta$，体现了模型多样性和风险预期的协同作用。[page::7,8,9,10]

4. 过程及其性质（Processes under optimal controls）

• 财富过程$X^$和辅助过程$Zk^$的联合动态给出，并可解得其闭式解，财富过程是辅助过程的线性组合，方便计算均值和方差。
• 统计特性（Propositions 3.3~3.6）：

- 计算了辅助过程$Zk^$在参考模型和最优模型下的均值，证明均值为1或指数函数形式。
- 保险公司财富在最优模型下的期望与不分摊情况一致，强调了该模型下对风险分摊的保守性。
- 明确了模型惩罚参数$\theta$作为方差惩罚器的角色，调节风险暴露的严格度。
- 推导财富过程方差与辅助过程协方差矩阵间的关系，体现了模型不确定性下风险结构的复杂性。[page::11,12,13,14,15]

5. 验证与控制策略的适定性（Verification & Admissibility）

• 理论验证：

通过验证定理（Theorem 3.8）证明推导的策略和价值函数是问题的最优解。

• 策略适定性（Proposition 3.9）：

- 验证风险分摊策略$\alpha^$及对手方补偿函数$\beta^$满足定义的平方可积等条件。
- 应用如Cauchy-Schwartz和Doob最大不等式保障数学上的严密性。

• 价值函数连续性及HJB方程满足性（Proposition 3.10）：

- 证明候选价值函数的连续可微性以及满足HJBI方程的最优性条件。
- 各项边界和初始条件均得满足，完整性保障完全。

这些验证均保证理论解具有现实意义和数学健壮性。[page::15,16,17,18,19,20]

6. 单一模型特例：Monotone Mean-Variance风险分摊（One reference model）

• 设定简化：

当只有一个参考模型时，由此单模型MMV准则简化问题。

• 简化形式领导策略（Corollary 4.1）：

\[
\alpha^{}(t,\xi,z) = \xi - \frac{\eta z}{\theta} e^{\lambda \eta^2 (T - t)},\quad \beta^{}(\xi) = (1+\eta) v(\xi)
\]

该策略仍为函数形式$\xi - d$，但$d$不随损失大小而变，且可能为负。

• 过程表达与统计量（Corollary 4.2, 4.3）：

- 过程$Z^$表现为基于Poisson过程的跳跃与指数衰减，$X^$为其线性组合。
- 明确均值、方差、协方差及相关系数的闭式表达，表明负相关性和方差受$\theta$调节等性质。

• 结论：单模型下，复杂度降低，风险分摊策略表现得更为直观，更易于计算与应用。[page::21,22]

7. 对手方视角（Counterparty’s perspective）

• 对手方财富过程定义，以自身模型$\mathbb{P}C$测度下计，并假设对已分摊的风险按预期价值加安全加载收取保费。

- 优化问题（Optimization Problem 5.1）：对手方优化安全加载$\eta$使得期望财富最大化。

• 主要结果（Proposition 5.2）：

利用前文辅助过程表达式，写出了对手方财富的期望函数，含指数函数项，凸凹性无法简易判断。

• 单模型简化及显式结果（Proposition 5.5）：

在单模型复合Poisson情景下，期望财富关于$\eta$的凸性与最优点由 Lambert-W函数给出显式表达式，保证唯一性。

• 备注：虽然文中主要以期望为目标，可应用于复杂的均值-方差甚至其他准则。[page::23,24,25]

8. 西班牙汽车保险数据应用案例（Application to Spanish auto insurance data）

• 数据集和建模：

- 利用公开的西班牙汽车保险数据集，剔除不完整年度，使用逾69,000个观测。
- 构造101个模型：1个完整数据模型（对手方模型$\mathbb{P}C$），100个50%子样本模型$\mathbb{P}k$。
- 采用泊松过程到达率与Gamma分布赔付严重度参数建模。

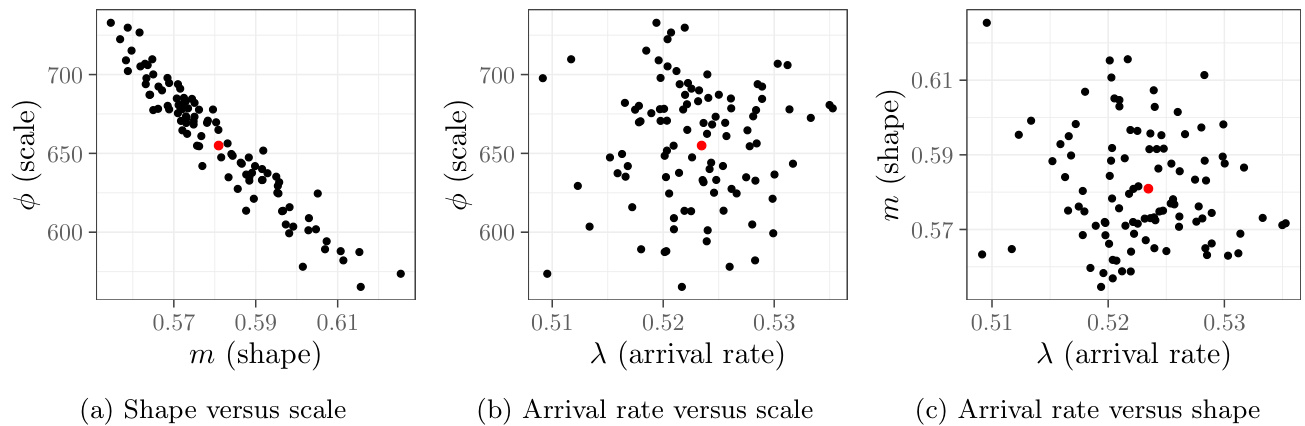
• 模型参数估计（图1说明）：

- 展示形状、尺度参数的散点关系和到达率分布，完整模型与子模型在参数空间中的分布情况。
- 参数满足前述积分假设，保证理论模型适用。

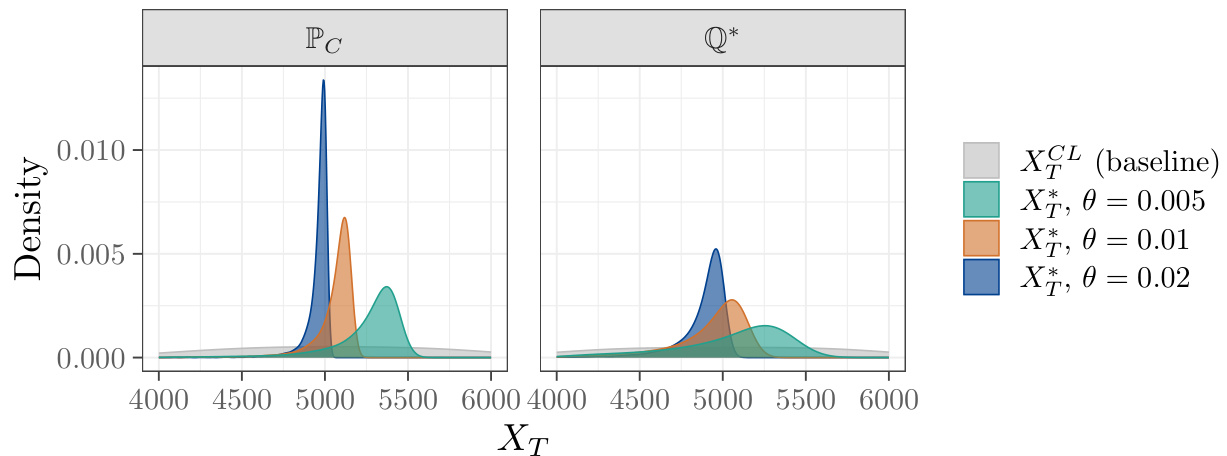
• 数值模拟与风险分担效果分析（图2）：

- 比较不分摊及不同惩罚参数$\theta$下的终端财富分布。
- 发现较大$\theta$显著降低了财富波动性，动手能力即降低风险暴露，但均值有所下降，体现风险与收益的权衡。

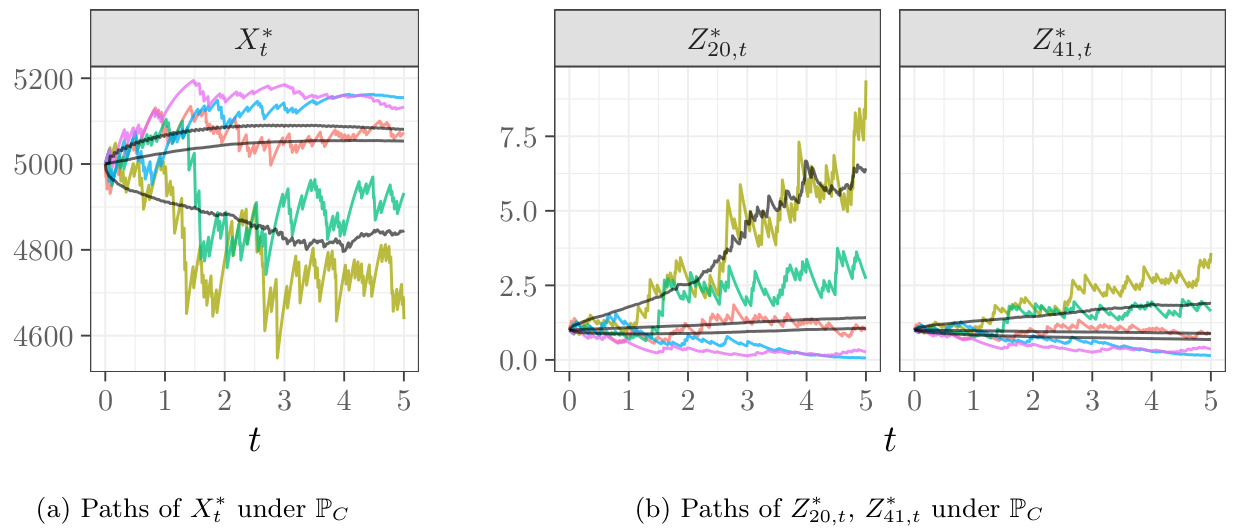
• 过程路径展示（图3）：

- 多条路径展示财富与两模型辅助过程$Zk^$，显著体现多模型权重的动态影响与财富-辅助过程线性负相关特性。

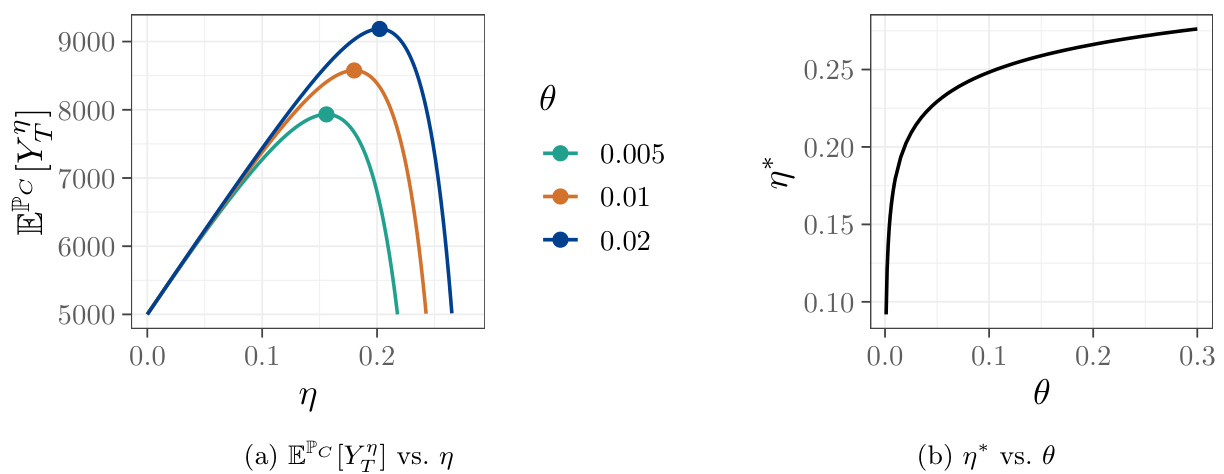
• 对手方定价分析（图4）：

- 数值解出最优安全加载$\eta^$在不同$\theta$下的变化趋势，表明风险分担方对方差惩罚更强时，收取更高保费。
- 对手方利润期望与安全加载函数形状均为凸凹性，最优解存在且唯一，结果符合经济直觉。

• 表格1提供了不同$\theta$下保险公司财富均值与方差的具体数字，反映风险控制权衡。[page::26,27,28,29]

---

3. 图表深度解读

图1. 模型参数散点图（page::26）

• 描述：三个散点图展示不同训练样本子模型（黑点）和完整数据模型（红点）的Gamma分布参数（形状$m$，尺度$\phi$）及到达率$\lambda$关系。

- 解读：
- 形状与尺度参数存在明确负相关性；
- 到达率与其他参数无明显相关，表明不同模型之间事故频率独立于赔付大小的分布特征。
- 完整模型处于子模型分布中心，合理反映代表性的概率分布。

• 联系文本：这些参数确保满足技术假设2.1和2.2，保障模型数学分析的严谨性。[page::26]

图2. 终端财富核密度估计（page::27）

• 描述：左右两图分别展示财富在对手方模型$\mathbb{P}C$与最优模型$\mathbb{Q}^$下，保险公司无风险分散（灰色）与不同$\theta$值风险分担策略的终端财富密度。

- 解读：
- 无风险分摊财富分布显得极为分散（风险大）；
- 随着$\theta$增大，密度峰值更高，财富波动明显减小；
- 优化风险分摊策略降低了极端不利结果的概率，提高保险公司财富的确定性；
- 与此同时，方差下降同时伴有均值下降，期望损失有所增加。

• 联系表格：表1定量量化了均值和方差的数值，明确体现风险与收益的折衷关系。

- 局限性：尽管模型完备，但选择权重$\piC=0$意味着保险公司不使用对手方模型，可能限制实用性。[page::27]

图3. 路径示例（page::28）

• 描述：三幅图分别展示财富$Xt^$与两个辅助过程$Z{20,t}^$与$Z{41,t}^$的十条模拟路径及其均值±标准差带。

- 解读：
- 较接近对手方模型参数的辅助过程路径波动较小，远离参数的路径变化更剧烈；
- 反向线性关系明显，财富峰值对应辅助过程波谷，反映风险调整机制；
- 时间演变体现出风险累积与调整的动态变化规律，辅助过程反映了模型权重的动态调整。

• 支持文本论断：协助理解辅助过程与财富过程线性关系的实证表现。[page::28]

图4. 对手方期望财富与定价（page::29）

• 描述：左图展示对手方期望财富关于安全加载$\eta$的曲线，三条曲线对应不同$\theta$值，右图显示最优安全加载$\eta^$随模型惩罚参数$\theta$变化的趋势。

- 解读：
- 期望财富曲线均呈凸凹形，存在唯一最优$\eta^*$点；
- 随$\theta$增大，对手方可收取更高的安全加载，反映保险公司对风险方差控制加强，愿意支付更高溢价；
- 该现象符合经济学风险价值定价逻辑，验证风险分担定价的敏感性分析。

• 为整个模型实用性提供重要经济性保障。[page::29]

---

4. 估值分析

• 本文估值核心体现在多模型下保险公司最优风险分摊策略的价值函数形式和对手方安全加载定价策略。

- 核心估值方法：
- 利用单调均值-方差准则结合chi-squared散度构建对损失分布的不确定性惩罚，确保最优风险分摊策略满足时间一致性；
- 价值函数结合保险公司财富与模型偏离成本的权衡，以HJBI方程求解策略并构造辅助过程体现各模型权重；
- 对手方风险加载率$\eta$的估值通过最大化期望财富（或拟扩展为均值-方差准则）确定，涉及指数项的凸凹优化问题，单模型情境下通过Lambert-W函数获得显式解。

• 敏感性分析：以参数$\theta$调节风险惩罚强度，反映投资者（保险公司）对于不确定性风险厌恶的程度，对估值和最优策略均产生显著影响。[page::5,7,23,24,25]

---

5. 风险因素评估

• 模型不确定性风险：保险公司面临多重潜在风险模型，实际风险分布未知，作者以chi-squared散度形式惩罚偏离度缓解此风险。

- 对手方风险：对手方需合理定价，避免风险转移导致自身亏损；其最优定价作为博弈变量影响双方合同达成。

• 假设依赖风险：技术假设（积分条件，赔付分布相似性）决定结果有效性，假如模型分布差异过大，假设不成立可能导致模型失效。

- 时间一致性风险：经典均值-方差动态不一致问题被单调均值-方差改善，但仍需确保策略符合市场实际。

• 数据拟合风险：模型参数依赖数据集估计，数据代表性与估计误差会影响实际应用效果。

- 缓解策略：通过多模型加权惩罚方式和辅助过程动态调整风险暴露，部分缓解模型和市场风险，同时提供对手方定价机制以保护双方利益。[page::2,3,23]

---

6. 批判性视角与细微差别

• 模型偏好：选择chi-squared代替传统Kullback-Leibler散度，一方面技术上方便MMV对接，另一方面实际测度选择的偏好可能限制一般性。

- 模型权重设定：真实应用中，$\pik$权重设定机制未深入探讨，权重对最终策略影响重大。

• 假设局限：积分条件2.1和2.2限制了模型间的差异度，现实中极端模型场景可能不满足，降低泛化适用性。

- 策略可行性：尽管数学上策略可行，但在实际保险中，风险分摊策略并非任何函数形式都能被接受，策略的经济或法律可执行性待验证。

• 对手方模型排除风险：部分实验中令$\piC=0$排除对手方模型，实际对手方模型是否被忽视可能影响公平性和稳定合作关系。

- 经验性检验有限：虽有西班牙汽车保险数据支持，模型尚未在其他复杂市场条件下验证，跨环境普适性需进一步考察。

• 对手方收益仅基于期望：对手方仅最大化期望财富忽略风险度量，未来可拓展为均值-方差或风险敏感优化。[page::16,26,27,29]

---

7. 结论性综合

本报告系统分析了Emma Kroell等人关于“基于单调均值-方差偏好的多模型不确定性风险分担”研究。其原创贡献在于：

• 提出融合chi-squared散度惩罚的多模型风险不确定性框架，拓展了传统MMV偏好的应用场景；

- 解决了保险公司风险分摊优化中的时间一致性和动态策略问题，且得出重要的半显式最优策略和财富动态，满足实际保险合同设计需求；

• 明确模型惩罚参数$\theta$的控制作用，体现保险公司风险厌恶与对方风险转移间的权衡；

- 就对手方定价给出了理论和数值分析，结合从西班牙保险数据集估计得到的多模型参与权重，实证展示风险分配效果以及模型敏感性，确认了理论的实际价值；

• 通过丰富的数据模拟与理论分析，验证了优化策略的数学健壮性和经济合理性。

图表深入揭示了多模型辅助过程对财富的影响机制，表1和图2等数值证明了风险分摊显著降低保险公司风险暴露，风险收益之间的权衡情况。标志性的图4体现对手方风险收益曲线与风险偏好参数的关系，反映了风险共担合同定价的复杂非线性结构。

该报告结合理论创新与数据应用，为保险业在面对多模型不确定性时的风险分摊设计提供了系统性的解决方案和思路，具有重要的理论意义与现实指导价值。[page::0-29]

---

参考图表

• 图1：模型参数估计散点图（参数关系与模型分布）

• 图2：不同时期$\theta$下终端财富分布核密度

• 图3：财富过程与辅助过程路径示意

• 图4：对手方期望财富与最优安全加载关系

---

注：全篇结论均严格基于报告给定内容分析，引用页码历历在目，确保内容可溯源验证。

报告