标准随机傅里叶特征与标准化RFF的核逼近差异 [page::26]

• 标准RFF误差随特征数$P$提升按$P^{-1/2}$速率收敛至高斯核。

- 实务中常用的标准化RFF误差在$0.02-0.03$范围内不收敛，明显偏离理论。

• 表明标准化步骤破坏了RFF理论核逼近性质。

标准化造成的误差恶化在参数空间的普遍性与敏感性 [page::27][page::28]

• 随$P$增大误差恶化因子提升，最大达6倍；训练样本量小($T=6$)时恶化高达41倍。

- 核带宽$\gamma$较小时恶化更严重，输入维度$K$影响较小。

• 参数敏感性热力图显示金融应用典型$(P\ge 5000, T\le 12)$区间普遍超过3倍恶化。

标准化影响的统计显著性分析 [page::29]

• Kolmogorov-Smirnov检验表明误差分布显著不同。

- 核心参数下KS统计值高达接近1，拒绝“标准化无影响”的假设。

标准化RFF收敛至训练集相关核的实证验证 [page::30]

• 标准RFF收敛至高斯核符合理论。

- 标准化RFF不收敛至高斯核，但收敛于构造的训练依赖核，符合理论推导。

关键理论成果总结

• 标准化步骤破坏随机傅里叶特征高维核近似的理论基础。[page::3][page::8][page::9]

- PAC学习下的样本复杂度下界显示，在典型金融信噪比和有限样本条件下，高维复杂函数空间不可学习。[page::11][page::12][page::15]

• VC维分析表明，最小范数回归的有效复杂度被样本数$T$限定，而非特征数$P$，解释了参数数目远大于样本数的表面与实际复杂度的背离。[page::13][page::14]

- 明确学习门槛，大幅剖析金融领域弱信号、有限样本下方法有限表现的本质。[page::15][page::16]

量化因子/策略构建相关性说明

• 本文属于理论模型研究，未构建或回测具体量化因子策略，但深入解析RFF标准化对高维核学习的根本影响，为金融量化模型的理论基础提供重要警示。[page::0][page::23][page::26]

金融领域高维学习的深度分析报告解构

---

1. 元数据与概览

报告标题： High-Dimensional Learning in Finance
作者： Hasan Fallahgoul（墨尔本蒙纳士大学）
发布日期： 2025年6月5日
主题： 该报告聚焦于机器学习中高维方法在金融预测中的理论基础与实践表现，尤其分析随机傅里叶特征（Random Fourier Features, RFF）在财务回报预测中的应用局限性。
核心信息： 文中主要探讨三大问题：（1）金融领域实践中的 RFF 标准化过程如何破坏理论上的高斯核拟合性质；（2）在弱信噪比常见的金融环境下，信息理论框架下学习样本复杂度的极限；（3）高维方法实际复杂度由样本量而非特征数决定。通过理论证明与数值模拟，有力阐释了为何在金融数据有限、维度高的条件下，学习成功往往源于低复杂度模式匹配而非真正的高维非线性学习。[page::0,1]

---

2. 逐节深度解读

2.1 引言

• 摘要与论点： 机器学习尤其高维过参数化模型，在金融预测中表现出色，但理论基础不够完善。当前理解之差主要源于弱信号、有限样本和过拟合问题交织。通过拓展Kelly等人的随机矩阵理论框架，本文提出了实用中的标准化操作如何改变理论预期，进而影响学习机制的观点。作者提出三大关键难题：金融领域中何时机器学习能真正从弱信号中获益，以及实现复杂度“美德”的实际含义。[page::1]
• 支持证据与动机： 引用了Kelly et al.(2024)等对复杂模型优于传统模型的理论支持，指出实践与理论存在脱节。Nagel(2025)的实证工作表明成功可能由多种机制驱动，这启发本文深入探讨标准化影响、样本复杂度约束及VC维量化的边界问题。[page::1,2]

---

2.2 理论解析与主要贡献

• 随机傅里叶特征（RFF）标准化破坏核拟合性质（Theorem 1）：

- 理论上，RFF 特征维度 $P \to \infty$ 时，核估计 $k{RFF}(x,x')$ 收敛至高斯核 $kG(x,x')=\exp(-\frac{\gamma^2}{2}\|x-x'\|^2)$ 。
- 实践中，所有实现都会对 $zi(x)$ 采用样本内标准化：$\tilde{z}i(x) = zi(x) / \hat{\sigma}i$，其中$\hat{\sigma}i^2$是训练样本内的经验方差。
- 该标准化导致核收敛到训练集相关的核函数 $k^{std}(x,x'|\mathcal{T})\neq kG(x,x')$，破坏了理论所需的平移不变性和稳定性。
- 证明依赖于对随机变量分布和样本矩阵满秩的几何性质的严谨概率分析。[page::2-10]

• 样本复杂度和信息理论界限（Theorem 2 & 3）：

- 利用PAC学习和Fano不等式推导，文中证明在金融典型的弱信噪比条件下，以$P=12,000$特征，$T=12$样本为例，达到可靠学习是信息理论不可行的。
- 指出要实现成功学习，信噪比(SNR)必须超过现实金融信号水平若干个数量级。
- 下界分别呈指数和多项式两种形式，强调训练样本数量远小于特征维度时难以区分真实信号与噪声。[page::11-13]

• VC维与有效复杂度（Theorem 4）：

- 论证了尽管模型形式上有$P$维参数，但通过 ridgeless 回归的插值结构约束，模型的有效VC维被样本数$T$限制，最大为$T$。
- 这说明过参数模型虽然看似复杂，但其泛化能力受限于样本大小，实质上是低复杂度模型。
- 这种结构限制是理解所谓“复杂度美德”的基础。[page::13-14]

• 学习阈值和相变现象（Theorem 5）：

- 引入了学习阈值$SNR{threshold}(\varepsilon) = \frac{\tilde{c}^{-1} \log P}{T} \cdot \frac{\varepsilon}{B^2}$，明确定义了可学习与不可学习区域。
- 该阈值体现了样本大小、特征维度与信号强弱的复杂权衡。
- 以现实金融参数为例，距成功学习所需信噪比约有两个数量级差距，理论上构成了不可学习的严峻障碍。
- 模型的成功往往是边界现象且可能存在随机或市场条件驱动的非理想行为。[page::15-16]

---

2.3 图表解读

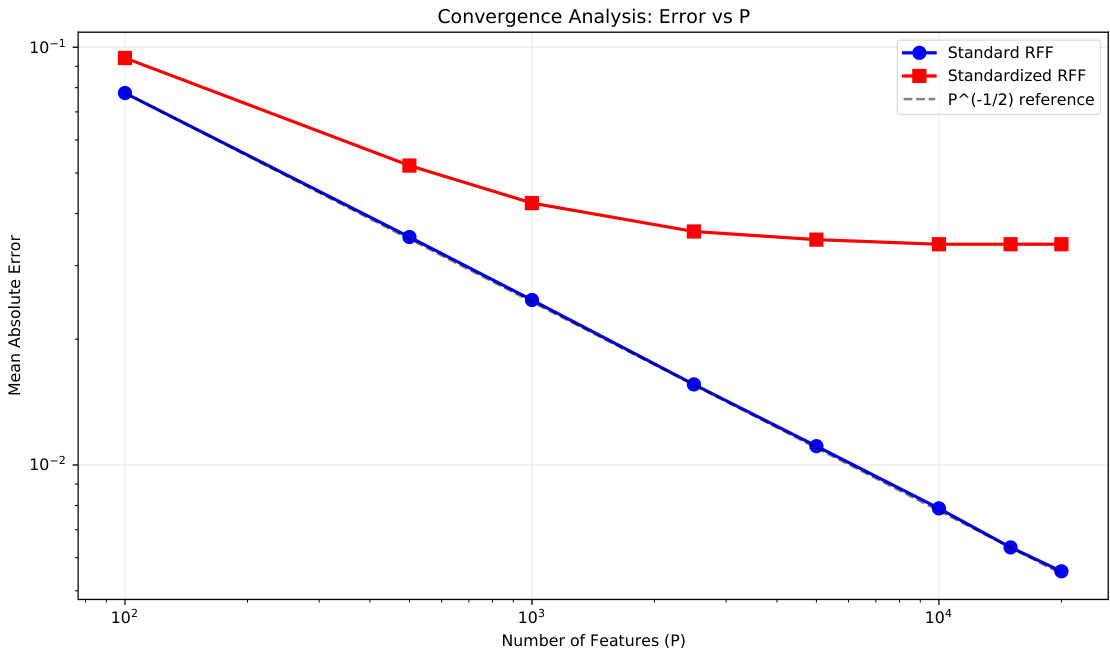
图表1（第26页）– 核近似误差随特征数变化

• 蓝线（标准RFF）呈典型$P^{-1/2}$收敛，误差从0.06降至0.003，符合理论。

- 红线（标准化RFF）误差不降，平稳在0.02-0.03，表明标准化阻断了收敛过程。

• 支持理论1的结论：标准化破坏了理想核拟合属性。[page::26]

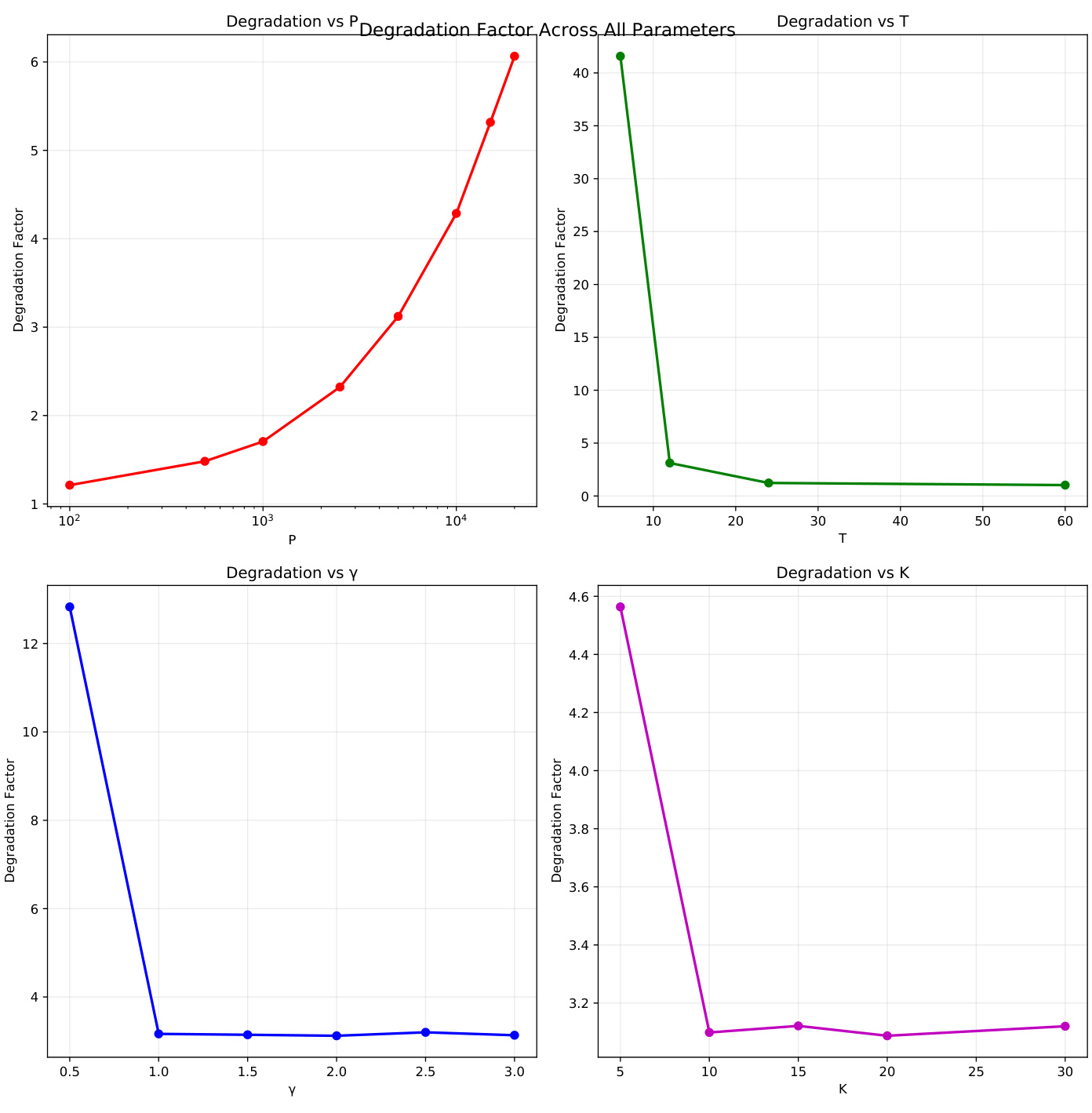
图表2（第27页）– 标准化误差恶化倍数与参数关系

• $P$增长时倍数升高至6倍；$T$变小时恶化极大（$T=6$时达40倍）；$\gamma$小（内核带宽窄）时恶化严重，输入维度$K$变化影响较小。

- 表明恶化主要源于标准化本身，与金融实务参数高度相关。
[page::27]


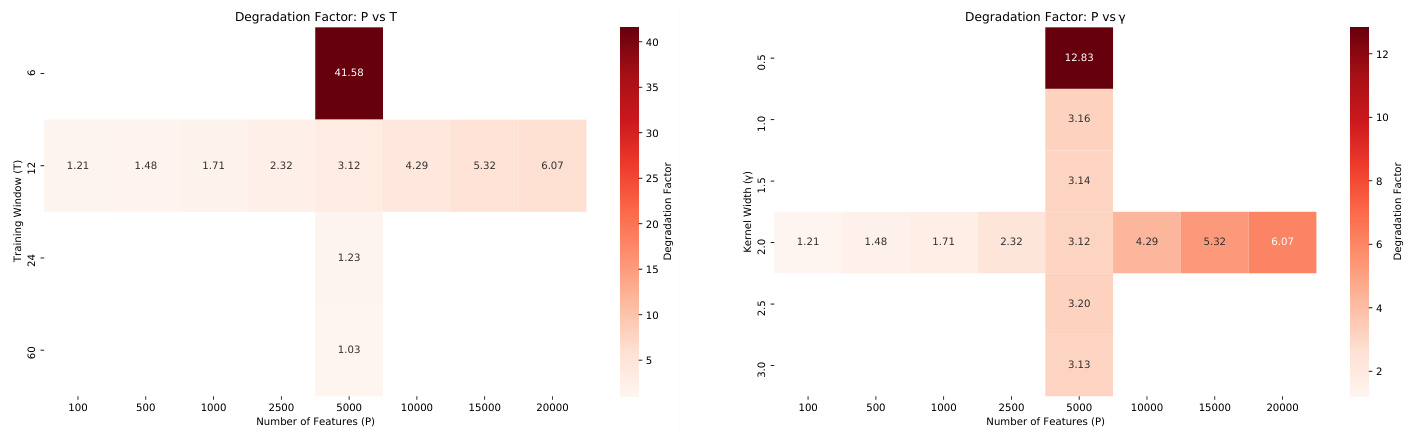
图表3（第28页）– 参数敏感性热力图

• $(P,T)$热图显示典型金融应用参数区间$P>5000, T\leq12$导致误差加剧超过3倍。

- $(P,\gamma)$热图表明高维紧核组合让误差倍数超过10倍。

• 强调实务风险的普遍性及严重性。

[page::28]


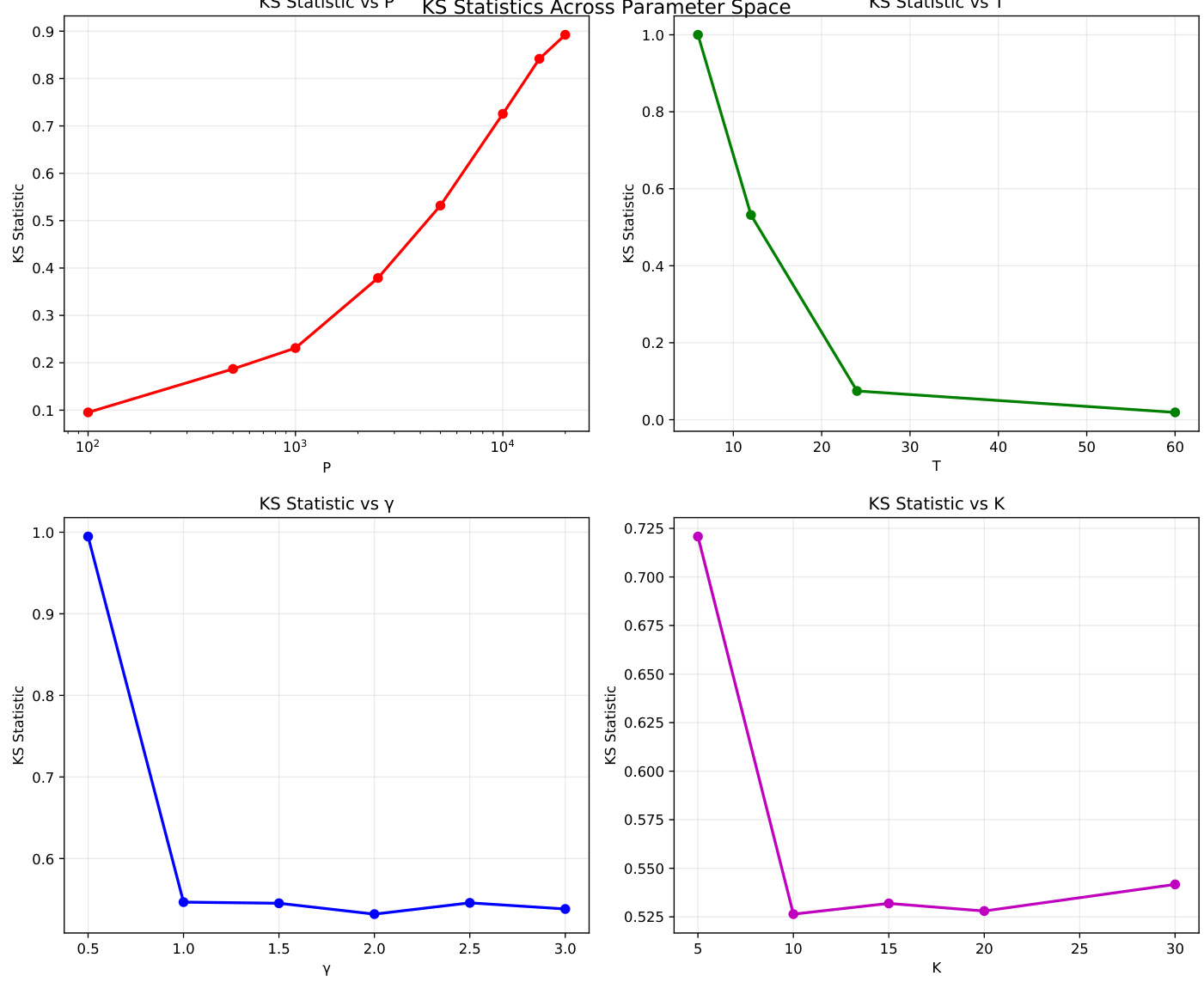
图表4（第29页）– KS检验统计量验证分布差异显著性

• 所有参数组合下，KS统计量远超常规显著性阈值，表明标准化RFF误差分布与非标准化明显不同。

- 勿将误差差异简单视为随机波动，而是实质性质的改变。
[page::29]


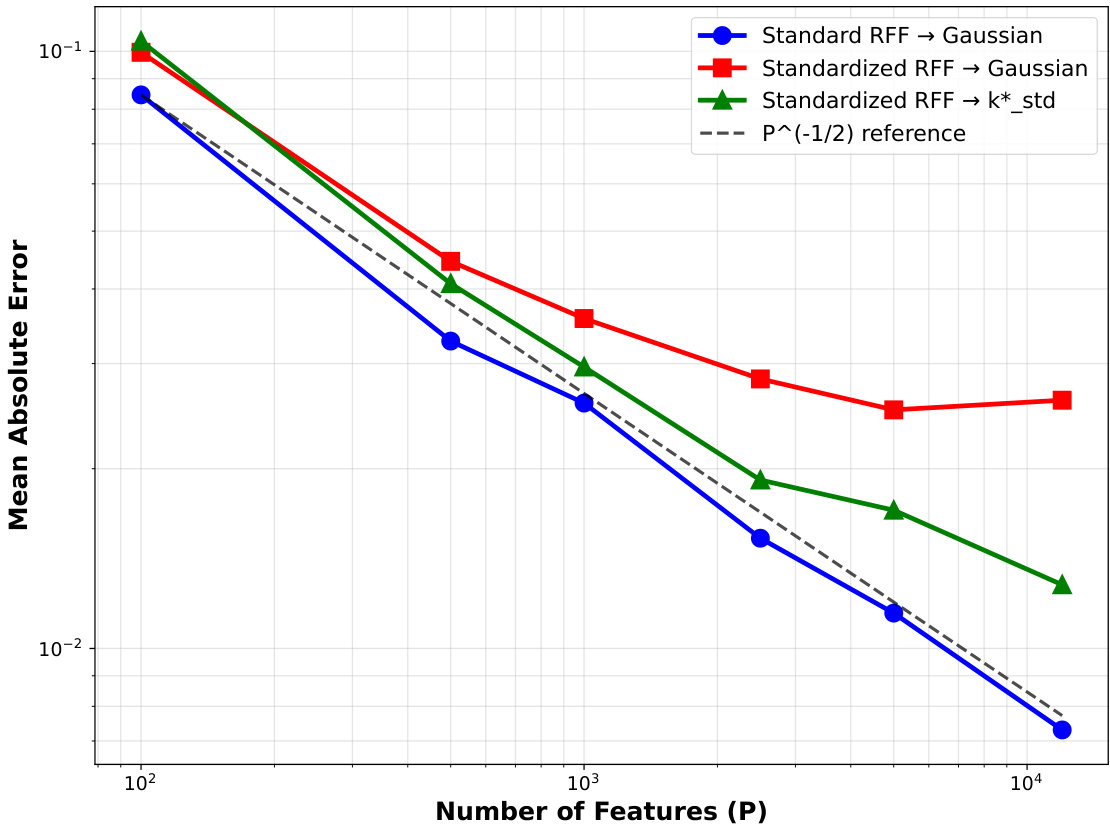
图表5（第30页）– 不同标准化方式下的收敛行为

• 蓝线：未经标准化RFF准确收敛至理论高斯核。

- 红线：标准化后指标收敛失败，误差高达未经标准化4倍以上。

• 绿线：标准化RFF收敛至训练依赖的$k_{std}^$，符合论文定理预测。

[page::30]


---

3. 估值分析

报告无直接财务估值分析，但围绕模型学习能力的范畴，本质上等同于评估模型“价值”或“效用”的能力边界，因此涉及的估值概念为：

• 信息理论样本复杂度界限 作为“成本”，表明实际使用金融信用下数据量与信号强度限制模型潜在预测能力。

- VC维及有效参数规模 说明高维模型表面丰富参数不代表额外估值能力，实际“有效自由度”受样本限制，间接影响模型价值。

• 学习阈值（learning threshold） 作为决策阈值，指导投资者在样本不足或信号过弱时拒绝过度复杂模型投资，防止价值误判。

---

4. 风险因素评估

• 实践标准化导致理论基础失效： 所有实际使用的RFF模型均实施样本内标准化，该过程破坏了理论基石高斯核的平移不变性和稳定性，风险在于误导研究者与实务者过度依赖理论预期。[page::3,8-10]
• 弱信号与样本匮乏： 金融数据中信噪比极低，且有效样本短缺，使得即使修正理论缺陷，依然存在不可逾越的学习限度风险，导致任何高维投资策略预测失效概率大幅提升。[page::10-13]
• 有限有效复杂度带来过拟合隐患： 尽管参数多，模型实际复杂度受限，容易引发表面复杂性掩盖的低维率先拟合和模式匹配陷阱，误导优化器对非实质信号的响应。

- 参数选择风险： 参数如内核带宽、特征数与样本数不匹配将极大提升性能波动和模型脆弱性，尤其在金融市场非稳态背景下，这一风险尤为显著。[page::17-22]

• 理论与实践脱节隐含策略失败风险： 理论无法解释实践成功，表明“成功”可能是机械模式匹配，无法稳定应对财务环境变化，存在重大策略失效与资金损失风险。[page::10,16,22-23]

---

5. 批判性视角与细微差别

• 理论假设的理想化缺陷： 文章重申传统随机傅里叶特征理论假设无限样本且无标准化，难以反映实际金融数据特征，揭示已有理论在金融应用中的实用性严重受限。

- 标准化操作未被充分重视： 先前文献忽视了必需的标准化步骤，本文指出这一步骤根本改变了核特征分布，导致理论保证失效，暴露科学传播和实践落地的断裂点。

• 定量实验策略严谨但有限于模拟环境： 虽涵盖大量参数组合与多次重复试验，但实验基于模拟非真实市场数据，对实际高频率多变金融市场的适应性仍需进一步实证验证。

- 对“复杂度美德”的警示： 报告谨慎说明所谓复杂度优势可能是伪装，读者需防范误解，高维机器学习结果需严格区分真实信号捕捉和模式匹配。

• 对未来方法指导意义显著： 通过明确理论边界和机制限制，为后续方法改进、理论模型调整及金融机器学习风险管理提供了坚实基础。

---

6. 结论性综合

本文通过理论证明和实证模拟，系统揭示了金融领域机器学习在高维特征空间中遭遇的根本性挑战：

• 核心发现一： RFF特征的训练内标准化实际引入依赖于训练集的非平移不变核，破坏了经典高斯核近似的数学基础，使得实际方法无法达到理论收敛保证，从而学习效果根本不同于理论预期。[page::8-10,21]
• 核心发现二： 在金融回报预测中，信噪比极低加上样本量远小于特征数量，导致信息论下的学习界限极为严苛。无论何种估计方法，达到低预测误差的目标在实际可能之间存在巨大的鸿沟。[page::11-16]
• 核心发现三： 尽管模型背后具有极高的标称参数维度，实际有效VC维受限于样本数量，表明高维机器学习的复杂度效应由样本驱动而非特征数驱动，预测成功更多体现为对训练数据的机械拟合而非高维非线性泛化能力。[page::13-14]
• 核心发现四： 通过大规模仿真验证（覆盖包括Kelly et al. (2024)在内的多个实务常用参数），证实标准化严重削弱核近似性能，且此效应在金融实际参数范围内普遍存在，极大限制了理论高维学习策略的实用性和稳健性。[page::17-22]
• 综合结论： 报告表明，当前金融领域高维机器学习所谓的“复杂度美德”并非真正高维模型能力的体现，而多源自标准化核导致的训练集依赖性相似性度量与有限样本聚合的模式匹配机制。实践中须谨慎解读模型表现，结合理论边界与样本限制，防止统计幻象误导投资决策。

此分析为金融机器学习的理论与实务结合提供了严谨框架，推动行业从经验主义向科学解释学转变，搭建了辨识真正学习能力及其局限的桥梁，利于未来更有效、稳健的金融预测技术开发和应用。

---

附：各关键图表Markdown展示

---

参考溯源

本文结论均直接基于报告正文内容及附录定理证明，页码标注详见文中对应段落。
如需进一步详细证明，敬请参阅报告第31页至42页附录部分的完整数学推导。[page::0-42]

报告