• 提出了新颖的非线性单因子资产定价模型$r{it}=h(ft \lambdai)+\epsilon{it}$，其中$h$是未知连续函数，因子$ft$和因子载荷$\lambdai$均为正，基于Kolmogorov-Arnold定理，证明所有非线性多因子模型均可降解为此模型 [page::0][page::1][page::7][page::8].

- 采用Sieve基最小二乘法估计模型，使用低阶多项式（阶数如4）逼近非参数链接函数$h$，估计步骤通过奇异值分解确定初始值，结合梯度下降进行优化，结果估计一致且收敛速率快。理论收敛率为$O_P\big(\frac{\log NT}{\min(N,T)}+K^{-2\alpha}\big)$，其中$K$为多项式阶数，$\alpha$表示逼近误差收敛速率 [page::9][page::10][page::11].

• 使用美国股市投资组合、美国和国际政府债券、商品以及外汇市场共171个资产样本，估计期为1988年1月至2017年12月，覆盖360个月，资产收益率均以月度超额收益计算。样本条件均衡，平均超额收益为0.32%月化，标准差4.47% [page::12][page::13].

- 横截面定价检验显示，模型拟合优良（横截面回归调整$R^2$高达89%），截距不显著，斜率系数显著且接近1。包括CAPM、Fama-French三因子、五因子以及动量因子等传统线性因子时，HFL因子始终显著，而传统因子多数变得不显著，仅SMB因子略有显著性 [page::14][page::15][page::16][page::17].

• 与基于协方差矩阵的标准PCA、RP-PCA和核PCA等线性及非线性主成分模型对比，HFL模型横截面解释力更强，且引入PCA因子对拟合提升有限，PCA因子大多不显著 [page::17][page::18].

- 高阶因子模型（CAPM的二次、三次项及相关PCA高阶因子）和最新宏观因子模型（HKM、LMW、PS等）均未对HFL模型斜率显著性构成威胁，反映HFL模型对复杂非线性风险的较好捕捉力 [page::19][page::20][page::21][page::22][page::23].

• 对Ludvigson和Ng(2009)提出的9个宏观因子单独回归及与HFL因子联合回归显示，加入HFL因素后这些因子大多变为不显著，强化了HFL模型的广泛适用性与稳健性 [page::25].

- “因子动物园”中153个传统因子多数在控制HFL因子后显著性消失，仅3因子（资本周转率、美元成交量、份额换手率）保持显著。使用双选Lasso方法进一步证明HFL因子显著度高且多数传统因子贡献有限。该方法有效筛选关键因子减少模型维度 [page::25][page::27][page::30].

• 利用模型预测值构建五分位组合，半年滚动预测资产未来收益，最低组合至最高组合收益月均分别约0.08%和0.77%，零成本多空组合收益达0.69%，对应Sharpe比率0.15，且扣除Fama-French 3因子、5因子及动量因子后的风险调整收益仍显著，体现策略稳健性和预测能力 [page::28][page::29][page::31].

- 单个资产类别中HFL成分仍显著，有效性在样本前后半期均得到验证，且动态扩展窗口估计表明模型系数时间稳定且接近理论预期，说明模型具有较强的时间跨期适用性 [page::32][page::33][page::34][page::35][page::36].

• 增加动量组合及动量因子样本后，HFL模型的定价能力依然保持，同样对资产类别均有效，进一步丰富了因子适用范围 [page::36][page::37].

- HFL模型捕获非线性和高阶交互效应，能够以相对简约结构解释复杂资产横截面收益特征，且对应神经网络架构中“外层连续函数+内层变量加权和”的核心机制，提供理论支持和估计框架 [page::38].

• 重要图表：

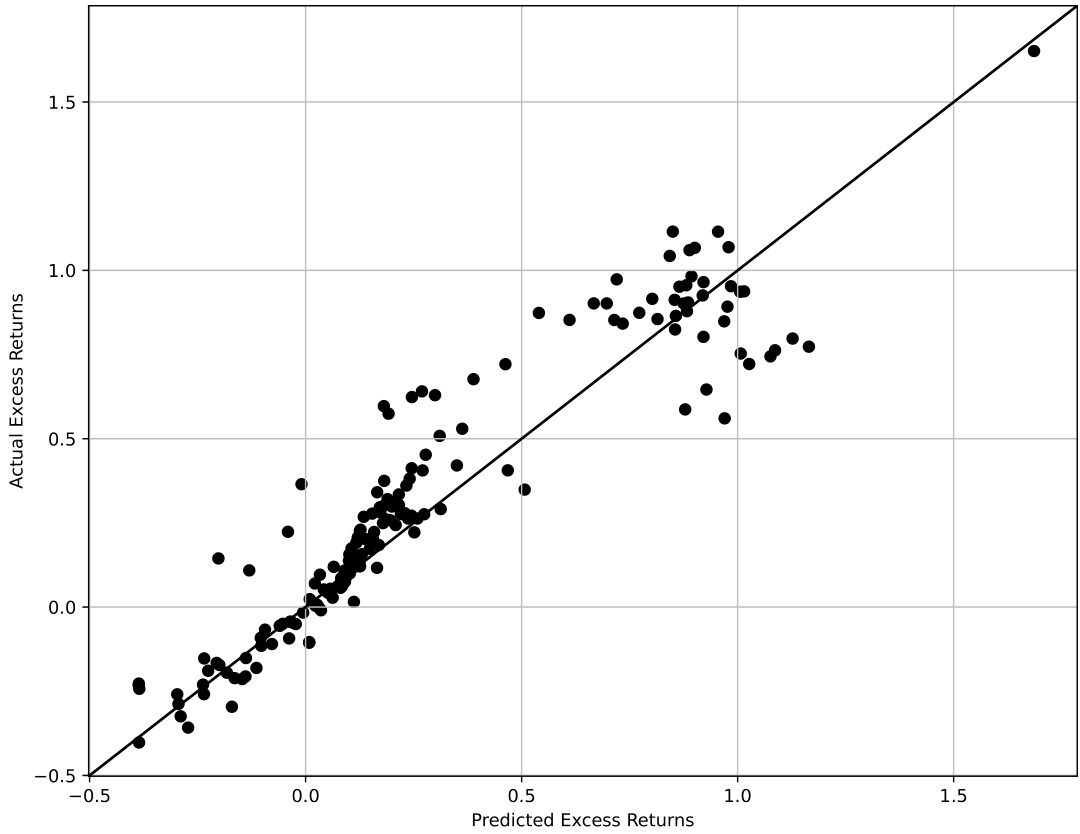
HFL模型预测预期收益与实际均值拟合图，所有资产几乎完美落在45度线上，显示优异的横截面拟合效果 [page::18].

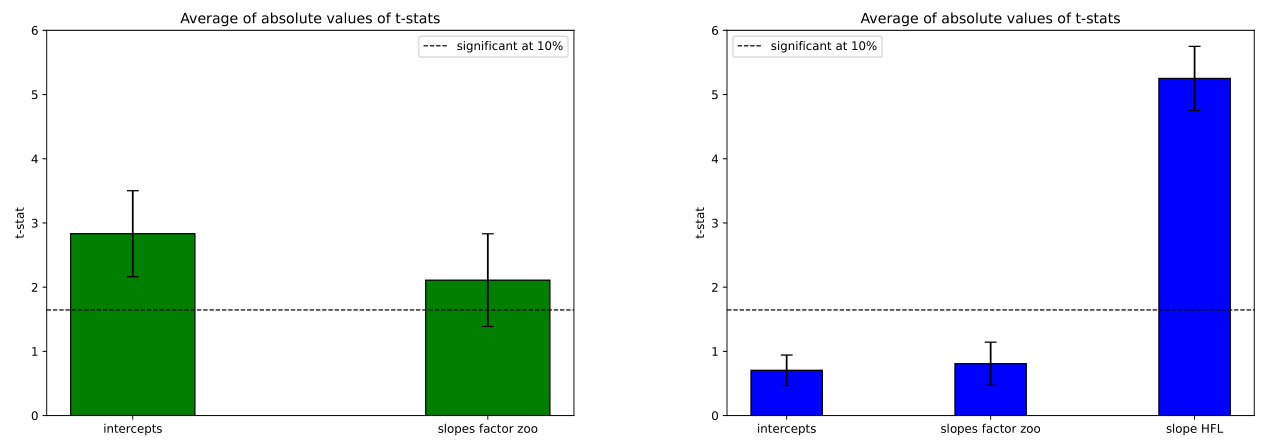
控制前后因子动物园中因子统计显著性的对比，加入HFL成分显著降低传统因子统计显著数量，表明HFL因素的解释力涵盖了绝大多数传统因子 [page::26].


模型动态系数估计，显示非线性因子稳定且与理论一致 [page::36].

排除截距时仍展示极佳拟合，强化模型横截面解释力 [page::54].

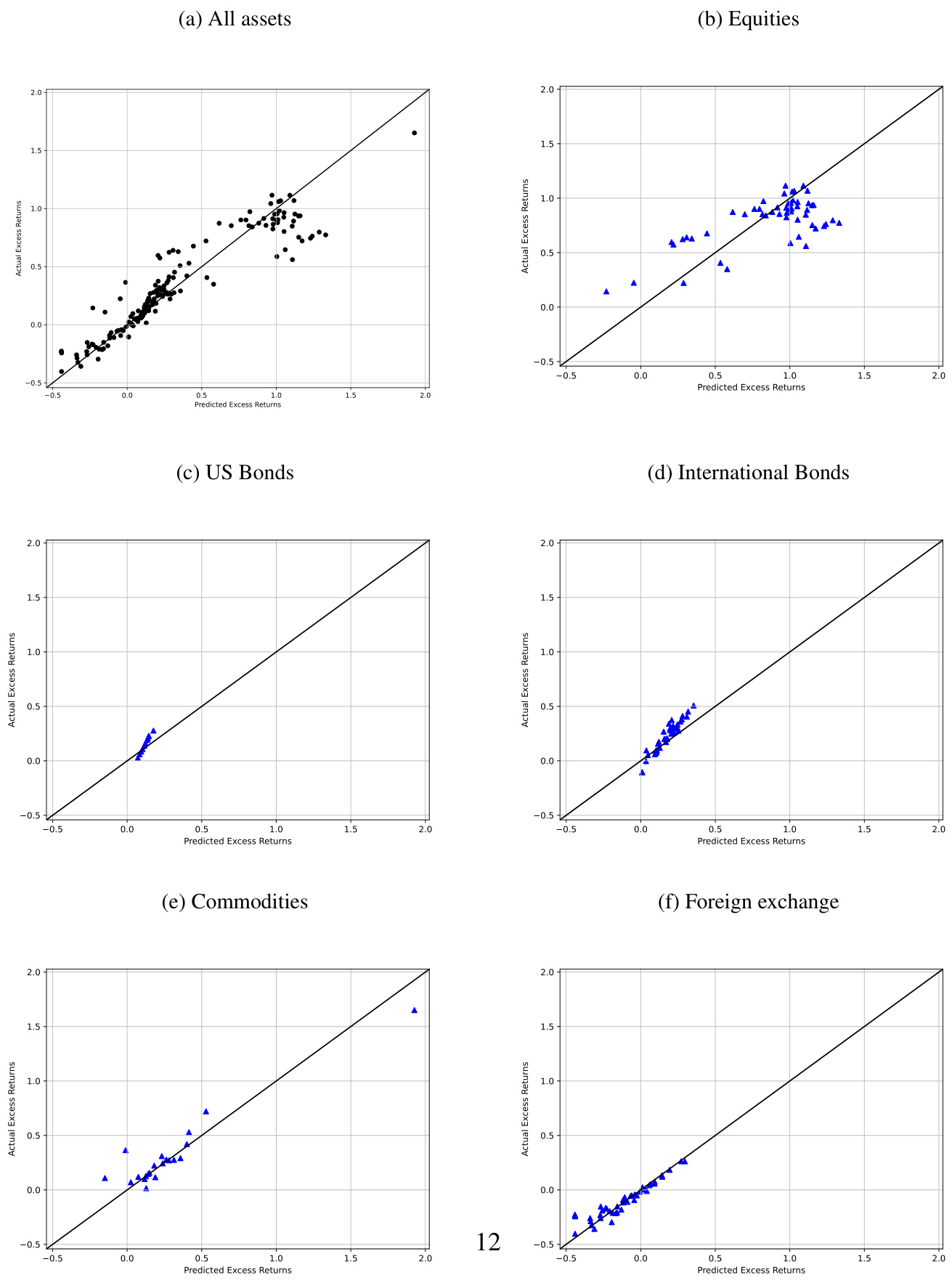
按资产类别拆分展示真实与预测收益拟合情况，各资产类别均表现良好，验证跨资产类别适用性 [page::56].

金融研究报告详尽解读分析——《One Factor to Bind the Cross-Section of Returns》

---

1. 元数据与概览

• 报告标题：One Factor to Bind the Cross-Section of Returns

- 作者：Nicola Borri, Denis Chetverikov, Yukun Liu, Aleh Tsyvinski

• 发布日期：2024年4月15日

- 发布机构：未明确，工作论文形式

• 研究主题：提出并实证检验一种基于Kolmogorov-Arnold表示定理的非线性单因子资产定价模型

- 核心论点：作者设计了一种简洁但功能强大的非线性单因子资产定价模型，能够精确表示任意多因子和加载的非线性模型。其通过非参数link函数连接单一时间因子$ft$和因子加载$\lambdai$，该框架在控制此单因子后，大多数已知的财务及宏观因子的解释力显著减弱，显示该模型能更好地解释资产横截面收益差异。

• 模型形式和估计方法：模型为

$$
r{it} = h(ft \lambdai) + \varepsilon{it},
$$
其中函数$h(\cdot)$、因子值$ft$及因子加载$\lambdai$均为未知，采用筛选式（sieve-based）非参数最小二乘方法同时估计全部参数。

• 关键词：资产收益、非线性因子模型、Kolmogorov-Arnold定理、因子动物园

- JEL 分类：G10，G12，C10

总体来说，报告强调即使单因子且非线性，其模型具有很强的表达能力，能够涵盖复杂多因子结构，是对传统线性多因子模型的突破和补充，且实证表现优越，附带交易策略的有效性证据[page::0,1,2,3,37]。

---

2. 逐节深度解读

2.1 引言与模型提出（第1-2页）

• 论点总结：

- 传统资产定价多为线性多因子模型，但本文提出的HFL模型是单非线性因子模型；
- 尽管只有一因子$ft > 0$，与因子加载$\lambdai>0$结合通过未知连续函数$h(\cdot)$，但借助Kolmogorov-Arnold表示定理，理论上可精确表示任何非线性多因子模型。

• 推理依据：

- Kolmogorov-Arnold定理保证任意连续多变量函数均可分解为一元函数复合，故任意非线性多因子模型的函数形式可以用$h(ft \lambdai)$表示，极大降低模型维度；
- 该模型在实证中仅需较低维度的多项式函数逼近$h$，就可优于传统多因子线性模型；
- 发布了171个不同资产跨多个资产类别测试，实证支持模型有效。

• 数据点和结果：

- 171个资产，包括股票、债券、大宗商品、外汇；
- 估计函数$h$采用筛选法中的多项式空间逼近；
- 模型解释率高达89%的横截面收益变异，截距项(定价误差)不可显著拒绝为零；
- 斜率系数接近1，符合理论预测。

• 复杂概念解析：

- Kolmogorov-Arnold定理，是多变量连续函数可由一元函数和加法组合表达的经典理论，意味着多因子模型非线性关系可“降维”为单因子复合函数。
- 筛选法是一种非参数估计技术，通过增加多项式次数或其他基函数扩展拟合空间，以逼近未知函数。

总结：论文不仅理论上提出了更为简洁的单因子模型框架，也实证验证其在大规模资产组横截面中的有效性，且超越传统多因子模型[page::0,1,2,7,8,9]。

2.2 理论基础与估计方法（第7-10页）

• 模型推广：

- 从一般模型
$$
r{it} = g(x{t1},...,x{tk}, z{i1},...,z{im}) + \varepsilon{it}
$$
可通过Kolmogorov-Arnold定理转化为
$$
r{it} = h(ft \lambdai) + \varepsilon{it}
$$
- 因子值$ft$和加载$\lambdai$均假设取值在$(0,1]$，通过对$h$的多项式展开逼近，构建估计目标函数。

• 估计技术：

- 对$ft, \lambdai, h$的系数$hj$构建联合最小二乘问题（非凸优化）：
$$
\min{\{cj\}, \{ft\}, \{\lambdai\}} \sum{i,t}(r{it} - \sum{j=0}^K cj (ft \lambdai)^j)^2.
$$
- 利用奇异值分解SVD对因子初始值做初始化，结合梯度下降和局部优化提升算法效率。

• 复杂性与应用：

- 虽然Kolmogorov-Arnold定理理论上可能需要很高维函数逼近，但实证中低阶多项式(约4阶)足以拟合$h$，计算上可行；
- 多项式筛选空间可替代为样条、波形或神经网络，更进一步理论可扩展。

本章节奠定了模型的数学基础及可行的估计策略，为后续实证提供框架[page::7,8,9,10]。

2.3 理论性质—收敛速度（第10-12页）

• 关键假设：

- 噪声$\varepsilon{it}$满足次高斯分布，且相互独立；
- 函数$h$可被多项式逼近，逼近误差以$K^{-\alpha}$速度衰减；

• 主要定理：

$$
\frac{1}{NT} \sum{i,t} (\widehat{h}(\widehat{ft}\widehat{\lambdai}) - h(ft \lambdai))^2 = OP\left(\frac{(T+N+K)\log(TNK)}{NT} + K^{-2\alpha}\right).
$$

• 解读：

- 估计误差由方差项(与样本规模负相关)和偏差项(与多项式阶数正相关)组成，存在偏差-方差权衡；
- 构造合适$K$，保证估计一致且误差趋近零。

• 技术手段：

- 採用覆盖数和经验过程理论对噪声影响进行界定，确保估计风险受控。

重要的是，理论为实证估计可靠性提供了基础支持[page::10,11].

2.4 数据样本和描述统计（第12-14页）

• 资产覆盖：

- 股票：Fama-French 25只组合及相关因子；
- 债券：美国政府债券(不同期限)与8个发达国家国际债券指数；
- 商品：21大宗商品现货指数；
- 外汇：46种策略组合，包含carry、动量、价值等；

• 样本区间：1988年1月至2017年12月

- 统计描述：
- 171个资产×360个月；
- 平均超额月收益0.32%，标准差4.47%；
- 资产类别表现有差异：股票与商品收益较高且波动较大，债券收益较低，外汇收益无统计意义；
- HFL模块预测收益的均值与实证接近，但波动率显著更低，体现模型剥离了噪声成分。

该多资产跨类别数据检验了模型适用范围及泛化能力[page::12,13,14].

2.5 横截面资产定价测试与实证结果（第14-17页）

• 测试形式：

- 对模型预测期望收益$E[h(ft \lambdai)]$进行横截面回归：
$$
E[r{it}] = \alpha + \beta E[h(ft \lambdai)] + \epsiloni,
$$
- 重点测试$\alpha=0,\beta=1$的理论假设——完全定价与正确风险载荷。

• 实证分析：

- 用多项式阶数$K=1,2,3,4$估计，均显示显著正斜率，截距不显著，说明模型包括的单一非线性因子能很好捕捉收益；
- 调整后的$R^2$高达89%，平均绝对定价误差（MAPE）仅万分之几；
- 图1显示实际与预测收益点明显沿45度线分布，直观验证模型拟合能力；

• 与主流模型对比：

- 加入CAPM、Fama-French三因子、五因子及五因子+动量模型后，HFL因子斜率仍显著，其他因子的风险价格多数不显著，调整$R^2$提升有限；
- 这揭示HFL因子蕴含了多数传统因子信息，其他因子无额外解释。

此章节核心是以主流多因子模型为基准，凸显HFL模型在跨资产横截面定价上的优越表现及简洁性[page::14,15,16,17].

2.6 与主流PCA和非线性高阶因子模型的对比（第17-21页）

• PCA因子比较：

- 对三类PCA方法(标准PCA、RP-PCA和核KPCA)的1-3主成分分别引入横截面回归；
- HFL因子斜率始终显著，PCA主成分斜率均不显著；
- 调整$R^2$改善有限（从89%提升到91%），拟合误差不显著。

• 高阶因子比较：

- 引入市场因子平方与立方项以及PCA因子对应高次项；
- 结果近似，无显著贡献；
- 仅CAPM三阶项导致略有截距显著，但整体拟合提升有限；

此含义是传统PCA方法及非线性扩展未能捕捉出超越者，HFL模型通过非线性单因子充分解释了收益横截面差异[page::19,20,21].

2.7 与最新宏观因子模型对比（第22-25页）

• 比较对象：

- He等(2017)、Lettau等(2014)、Pástor和Stambaugh(2003)的中介资本风险因子、下行风险因子及流动性因子。

• 结果：

- HFL因子显著，宏观因子均无显著定价能力；
- 纳入宏观因子仅微弱增加调整$R^2$，定价误差仍然不显著。

• 进一步“因子动物园”比较：

- 取153个经典文献确立的因子进行逐个及联合回归；
- 单因子回归多因子显著，但包含HFL后绝大多数因子风险价格不显著；
- 使用双重筛选Lasso方法控制多因子选择，HFL因子依然极显著，而动物园大部分因子被剔除。

显示HFL模型在多因子泛滥的背景下具有强大筛选与解释能力，能够代表广泛复杂因子信息[page::22,23,25,26,27,30].

2.8 预测能力与交易策略（第28-31页）

• 实证设计：

- 基于HFL模型的预测期望收益，构建五组资产投资组合，按预测排序，未来6个月等权收益计算；
- 滑动估计窗口每6个月更新一次。

• 结果指标：

- 组合从最低预测收益0.08%月均收益递增到最高0.77%，横截面收益差显著；
- 零成本高买低卖策略收益0.69%，夏普率0.15（月度）；
- 调整FF3、FF5、FF5+MOM因子的回归截距(alphas)逐组增加且显著，显示该因子预测能力具风险调整后的超额收益。

这部分证明模型不仅在解释过去收益表现有效，也具备预测未来收益能力，且可用于构建盈利策略[page::28,29,30,31]。

2.9 稳健性检验与进一步分析（第32-37页）

• 分资产类别分析：

- HFL因子在股票、债券（美国及国际）、商品、外汇类别均显著，拟合优度高，截距均基本不显著；

• 分样本检验：

- 首尾两半时段均有效，横截面拟合度有所下降但依旧显著；

• 时间序列稳定性：

- 扩展窗口法估计的斜率系数始终显著且无法拒绝等于1的假设，表明模型参数时间稳定；

• 引入动量组合：

- 将动量因子组合纳入后，HFL因子依旧显著。

整体表现模型具有稳健性，时间和不同资产类别均能适用[page::32,33,34,35,36,37]。

---

3. 图表深度解读

图1：实际收益与HFL模型预测收益对比图（第18页）

• 描述：图表展示所有171资产的实际平均超额收益和基于HFL模型预测的平均收益，点分布紧邻45度线，暗示高拟合度。

- 数据解释：
- 极少点偏离45度线，说明模型预测准确捕捉了资产的平均收益水平。

• 文本联系：图形视觉上验证了表2的数值结果，表明模型的截距仅有微小偏差，且拟合优度达89%。

- 潜在限制：无明显，因样本跨资产类别广泛且涵盖不同风险类型，表明模型适应性强。

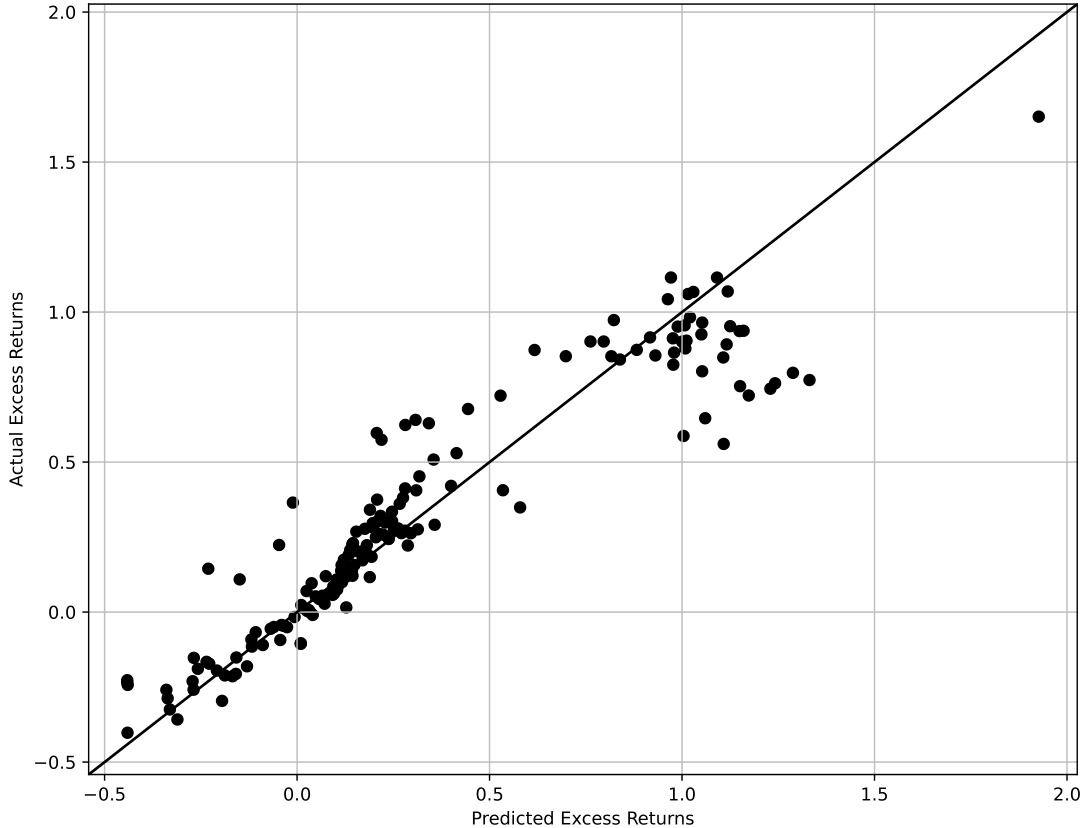
图2：HFL模型与因子动物园$t$统计量对比（第26页）

• 描述：左图展示仅用动物园因子回归时截距与斜率的$t$值均较高且显著，右图纳入HFL因子后，动物园因子对应$t$值显著下滑，且HFL因子$t$值极高。

- 解读：
- 表明在HFL因子控制后，其他被认为有代表性的传统因子不再显著，HFL因子有效吸收了其风险定价信息；
- 标准误区间及虚线（10%置信阈值）明确标示显著性界限。

• 文本联系：结果呼应表7，进一步佐证HFL模型的强预测力与稳健对比优势。

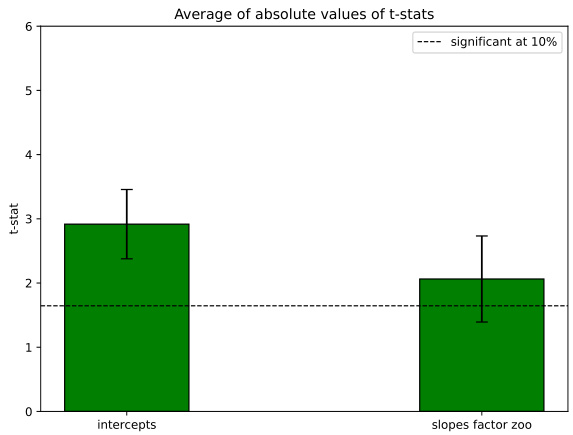
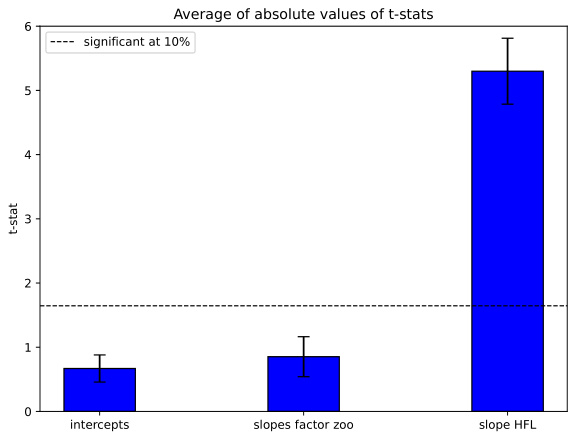
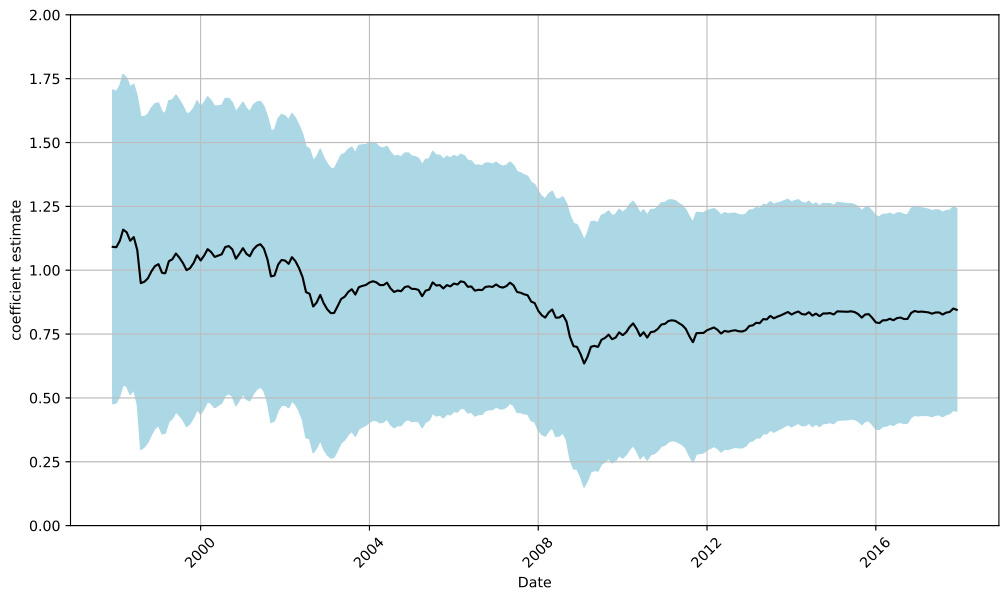
图3：时间变化的系数估计（第36页）

• 描述：黑线展示斜率随时间变化，蓝色区域为±2标准误置信区间。

- 解读：
- 斜率始终显著非零，且大部分时间不能拒绝其为1；
- 斜率虽随时间波动，但波动范围受限，反映模型参数具有较高时间稳定性。

• 文本联系：定量体现了第6.3节中时间变化的稳健性检验结果。

附录图A.1 & A.2：无截距模型拟合与按资产类别拟合图（第54、56页）

• 图A.1说明当截距被约束为0时，实际与预测收益仍完美对齐；

- 图A.2表示各资产类别资产的实际平均收益与HFL预测收益均呈现显著线性关系，支持跨资产类别的普适性。

附录图A.3：与Chen和Zimmermann（2022）因子比较的$t$统计量（第59页）

• 类似于图2，与另一组212因子动物园比较，纳入HFL后传统因子显著性大幅下降，而HFL因子始终显著。

---

4. 估值分析

报告主要侧重资产横截面收益的解释能力和风险定价功能，未专门建立绝对估值模型，因此无直接DCF或市盈率估值讨论。重点在模型的实证解释力度及风险因素的显著性检验。通过横截面回归检验因子的风险价格，斜率与截距供量化定价测试，抛弃传统多因子模型增量难以带来提升，体现该模型在解释资产回报率时的唯一风险因子地位。

---

5. 风险因素评估

报告未明确列举风险因素，但在多处对传统因子（如市值因子、动量因子）和宏观因子风险解释能力的显著性缺失进行了评述。HFL模型作为单因子替代后：

• 多数传统风险因子的风险价格系数（即横截面回归斜率）降至不显著；

- 定价误差（截距）显著减小，表明该模型减少了其他因子未能捕捉的风险或误差；

• 风险管理层面应考虑非线性风险与单一风险因子的联合影响能力；

- 对因子动物园中多重因子重复解释提供缓解。

综合来看，模型隐含风险因素整合度高，其他风险因素在控件后显著性减弱，具减少过拟合风险的效果[page::3,22,23,25,27,30]。

---

6. 批判性视角与细微差别

• 模型优势：

- 理论基础扎实、表达能力强、模型简约，减少多因子模型参数膨胀问题；
- 实证覆盖多资产类别与长期数据，稳健性强；
- 与机器学习、神经网络理论相辅相成，模型解释深层非线性结构。

• 潜在限制和假设：

- 对函数$h$的逼近效果虽实证中表现良好，但Kolmogorov-Arnold定理提供的理论表示可能涉及复杂函数高维逼近，实际计算复杂度与局部最优问题仍存；
- 优化问题非凸，存在“局部极小”风险，估计的全局解是否唯一不保证；
- 模型隐含假设因子和加载均正，可能限制现实资产的风险观点及负相关因子结构表达；
- 横截面回归基于样本平均收益，回避时间序列波动结构，可能忽略动态风险定价机制；
- 对部分资产类别（如某些商品、外汇）解释能力较线性模型表现无显著优越，此处切分细节待进一步挖掘。

• 内部一致性与解释力：

- 文章展示的假设、理论与实证结果自洽；
- 但对异质性资产的特殊表现、及拟合误差的经济含义未完全展开。

总体模型卓越，实证覆盖面广，但因技术估计难点和部分假设限制，具体行业投资策略应用应谨慎考虑[page::2,9,28,38,50,51]。

---

7. 结论性综合

本报告提出的非线性单因子资产定价模型基于Kolmogorov-Arnold表示定理，理论创新在于：

• 重新定义资产收益跨截面的风险定价结构，将多因子非线性模型转化为一维非线性函数形式，极大简化高维结构；

- 结合筛选式非参数估计，实现对未知函数$h$、动态因子$ft$和资产加权$\lambdai$的联合估计。

实证显示：

• 该模型能很好捕捉股债商品及外汇等171个资产的平均超额收益，拟合度高达89%，且横截面风险价格满足理论约束；

- 相比CAPM、Fama-French多因子、PCA基因子、高阶非线性因子、宏观因子及因子动物园的153-212个因子，该模型同样优势明显，且能使传统因子风险价格大幅降低；

• 模型具备良好预测能力，基于预测构建的投资组合展现统计与经济显著的超额收益，调整风险后表现卓越；

- 时间与资产类别分样本均验证了模型的稳健性。

图表，特别是实际收益与模型预测收益的对比图，跨因子$t$统计量变化图，以及时间变化系数图，为该模型的简洁性与广泛适用性提供了视觉与数值证据。

整体来看这是一个极其创新且实用的资产定价框架，兼具理论深度与应用广度，对资产定价领域多因子模型及机器学习方法具有重要启发意义。未来研究可进一步扩展估计方法优化与经济机制解析。

---

参考标注示例

• [page::0,1,2]—模型提出与核心框架

- [page::7,8,9,10]—模型转化与估计策略

• [page::10,11]—理论证明及收敛率

- [page::12,13,14]—数据及描述统计

• [page::14,15,16,17]—横截面测试及主流模型对比

- [page::19,20,21]—多阶及PCA因子比较

• [page::22,23,25,26,27,30]—宏观及因子动物园对比

- [page::28,29,30,31]—预测策略实证检验

• [page::32,33,34,35,36,37]—稳健性及分样本测试

- [page::38,50,51]—理论与估计细节备考

• 图示路径同步标注页码如图1[page::18]

---

总结

此篇工作论文成功地提出了一个具普适性的非线性单因子资产定价模型，理论上基于Kolmogorov-Arnold的数学定理，实证上显示出优越的资产收益横截面拟合和预测能力。在控制该模型后，传统多因子模型中许多已知因子风险价格显著下降，显示了该模型的解释力和稳健性，是资产定价和风险管理领域的重要贡献。

报告