• 模型设定与基本假设 [page::0][page::2][page::3]：

- 经纪商、知情交易者和非知情交易者的交易速度分别为$\nu,\eta,\xi$，三者均为平方可积进程。
- 价格过程包含信号项、价格冲击项（瞬时和瞬态，采用指数衰减的冲击核）及马丁格尔噪声。
- 库存与现金过程的动态精确刻画，包含即时交易成本$a,b,c$ 及库存罚款参数$\phi,\psi,r^{B},r^{I}$。
- 非知情交易者交易速度为外生均值回复过程。

• 性能指标及纳什均衡定义 [page::3][page::4]：

- 经纪商和知情交易者分别最大化自身财富减去库存风险罚项的期望收益。
- 纳什均衡为双方在对方交易速度固定时的最优应对。

• 性能函数严格凹性及Gâteaux导数推出最优策略的FBSDE表述 [page::5][page::6][page::7][page::8][page::9][page::10][page::11]:

- 性能函数对对应交易速度严格凹，保证唯一最大化解。
- 经纪商和知情交易者的最优交易策略分别由线性FBSDE系统描述，包含库存和价格影响耦合效应。
- 过程中的辅助变量定义及与价格冲击的关联表达式。

• Nash均衡的存在唯一性条件及等价非Hermitian矩阵Riccati微分方程 [page::12][page::13][page::14][page::15]:

- 纳什均衡由耦合FBSDE系统给出，该系统存在唯一解等价于对一非Hermitian Riccati方程的解的存在唯一性。
- 小时间窗条件下通过Banach不动点定理可判定存在唯一解，明确了时间窗上界及参数依赖条件。

• 闭式解构建思路及计算方法 [page::17][page::18][page::19]:

- 采用线性关系猜想，令交易速度过程为前向过程与状态变量线性组合。
- 相关矩阵微分方程及线性BSDE求解方案。

• 特殊情形及与文献比较 [page::18]:

- 当瞬态冲击衰减率$\mathfrak{p}$与经纪商运行罚项$r^{B}$均为零，不需额外参数限制即可保证解存在唯一。
- $\mathfrak{p}=0$时结果与Bergault和Sánchez-Betancourt(2024)中描述的均衡相匹配。

• 数值模拟结果分析 [page::20][page::21][page::22]：

- 在信号$\alpha$为均值回复过程的环境下，知情交易者和经纪商的最优交易速度与库存均随时间变化明显，带有5%和95%的置信区间。

- 随着价格冲击衰减速率$\mathfrak{p}$增加，经纪商库存曲线收敛于零附近，知情交易者库存初步收敛后在较大衰减时反而波动扩大。

- 纳什均衡与Cartea和Sánchez-Betancourt(2022)的两阶段优化模型比较显示：知情交易者平均市值增加约4.5%，经纪商则减少约5.5%[page::20][page::22]。

• 量化策略视角：

- 报告从博弈论视角解决了经纪商与知情交易者的动态互动，提出的FBSDE及矩阵Riccati方程解决方案本质构建了一种结合市场冲击、信息流和库存风险控制的动态量化交易策略框架 [page::3][page::5][page::12][page::17][page::20]。

金融研究报告详尽分析报告

---

一、元数据与概览

报告标题： Nash Equilibrium between Brokers and Traders
作者： Alvaro Cartea, Sebastian Jaimungal, Leandro Sánchez-Betancourt
机构： Oxford大学数学研究所，Oxford-Man量化金融研究所，多伦多大学统计科学系
发布时间： 未明确具体日期（至少不晚于2024年中，依据文献和引用时间推断）
研究主题：
研究经纪人（Broker）与其客户（信息交易者和非信息交易者）之间在充满价格冲击的交易环境下的完美信息纳什均衡策略。模型涉及场内公开交易所和场外交易两种市场机制，重点解决经纪人如何通过内部化和外部化交易及对冲策略来管理库存风险和利用信息优势。

核心论点与信息：
报告中作者建立了一个带有瞬时和瞬态价格冲击（采用指数衰减模型）的交易框架，在此框架中，经纪人兼顾两类客户的交易，且交易者行为组合构成一个随机动态博弈。通过将纳什均衡策略刻画为一个耦合的前向-后向随机微分方程（FBSDE）系统的解，报告不仅从理论层面刻画了平衡交易策略，还提供了显式的解析解。模拟结果揭示了信息程度、利润驱动和库存控制参数如何影响各参与者的策略和业绩表现。

---

二、逐节深度解读

1. 引言（第0-1页）

关键论点：

• 将经典经纪人-交易者模型扩展到存在瞬时和瞬态价格冲击的 OTC（场外交易）市场及公开交易所中。

- 经纪人面对一位资讯充分的交易者和一位非策略性交易者，同时也执行场内交易以管理自身库存风险。

• 利用前人工作（Cartea and Sánchez-Betancourt 2022）框架，结合Obizhaeva-Wang型价格冲击模型，突出及时性及衰减特征。

- 采用Gâteaux导数建立纳什均衡的最优响应关系，引出FBSDE系统描述策略。

• 该问题包含经济学和市场微结构的多个经典模型基础，同时因引入了瞬态冲击、实时信息交互和动态库存约束而具有创新。

逻辑与假设支撑：

• 假设交易速度控制在平方可积空间内，确保数学分析的正规性和解的存在。

- 交易信号的动态影响（信号驱动价格）与价格冲击相结合，体现真实市场价格波动机制。

• 库存风险通过二次惩罚项建模，既保护经纪人免受剧烈风险影响，也反映交易者对风险容忍度的现实考量。

---

2. 模型设定及性能指标（第2-4页）

核心论点：

• 建立经纪人和两类交易者的库存和现金流程动态方程。

- 中价过程由初始价、信号过程、价格冲击过程和马丁格尔噪声叠加构成。

• 价格冲击以微分方程形式定义，体现即时交易对价格的影响及随时间的指数衰减。

- 引入交易成本a,b,c，分别适用于经纪人、自有信息交易者及非信息交易者。

• 绩效指标总结为期望终端现金+库存市值-库存罚金项，平衡了利润和风险管理。

- 对性能指标的有限性进行了严格证明，保障了模型的数学健壮性。

• 纳什均衡定义为两方策略皆为对方最优响应，不可单边提升绩效。

关键数据点与假设：

• 价格冲击和信号过程假设平方可积及渐进独立性保障了处理的便利性和模型适用性。

- 库存惩罚系数非负，意在限制过度持仓风险，保证问题的凸性。

• 假设a > 转移参数乘交易时间，保障性能指标严格凹性，为存在唯一均衡奠定基础。

---

3. 纳什均衡的刻画（第5-13页）

3.1 函数严格凹性与Gâteaux导数的运用

• 证明对固定经纪人交易速率，信息交易者的绩效泛函对其速率严格凹；反之亦然。

- 使用函数分析中Gâteaux导数定义形成本轮最优响应策略。

• 这一步骤关键在于凸分析和变分求解方法，确保纳什均衡可以通过一阶最优条件识别。

3.2 最优策略的FBSDE表达

• 经纪人和信息交易者的最优交易速率皆满足耦合的FBSDE系统，表现为前向库存动态与后向影子价格共同驱动。

- 这与经典的前向-后向随机微分方程理论一致，提供了随机动态游戏的解构框架。

• 马丁格尔项体现交易中的随机性和信息渐进开放过程。

- 确定性边值条件（终端库存惩罚）导向具体的边界条件，这一设计保证解的唯一性。

3.3 纳什均衡的存在与唯一性

• 将复杂的FBSDE系统转化成矩阵形式，明确系统的系数矩阵。

- 使用典型的固定点理论和观测矩阵不等式，给出时间窗及参数大小的适当约束。

• 同时，论文运用非Hermitian矩阵Riccati微分方程理论步骤，证明在无瞬态冲击（衰减）及无运行库存惩罚的特殊情况下，解存在且唯一。

- 该结果严格涵盖数学中的前沿热点，保证理论模型在特定参数域的可解性。

---

4. 闭式解与矩阵Riccati微分方程（第14-20页）

4.1 非瞬态冲击、零运行惩罚的显式解构造

• 对模型矩阵结构分析，验证正定性及矩阵不等式条件，保证使用Freiling等人的非Hermitian矩阵Riccati方程理论。

- 解以矩阵分块形式表示并满足线性微分方程组，兼具稳定性和连续性。

4.2 与此前文献的联系

• 当瞬态价格冲击衰减率为零时，模型与之前的mean-field Nash均衡模型对应，对应参数和函数映射一一对应，理论连贯。

- 条件放宽后，解的存在仅需部分温和参数约束，进一步显示本模型的适用范围和稳健性。

4.3 BSDE终端解的表达及Nash策略的最终构成

• 利用积分与鞅的性质，将伴随BSDE转换成辅助ODE与随机积分的显式计算形式。

- 通过此方式，所有平衡策略均可以明确定义为线性映射，各量化函数通过确定性ODE系统计算得出。

• 清晰描述了策略如何依赖于信号动态、非信息交易的扰动以及经纪人的价格冲击反馈。

---

5. 数值实验（第20-22页）

数值实验参数选择及假定：

• 时间窗$T=1$，高频离散步长，百万次蒙特卡洛仿真。

- 设定库存终端惩罚为1，瞬时价格冲击参数$b=10^{-3}, a=1.2\times10^{-3}$。

• 运行库存惩罚项关闭，转瞬即逝价格冲击速率$\mathfrak{p}=0$（无衰减）。

- 价格信号及非信息交易者的交易速率均服从奥恩斯坦-乌伦贝克过程（OU），体现均值回复特性。

• 三个布朗运动相互独立。

关键发现：

• 仿真样本路径揭示由信号直接驱动的交易速度$\eta^$和$\nu^$，以及对应的库存变化正向响应，展示了模型现实性。

- 随着瞬态价格冲击衰减系数$\mathfrak{p}$增加，经纪人库存波动趋于平稳集中，而信息交易者库存在中值出现先收敛后波动加大的趋势，即策略稳健性受冲击衰减影响显著。

• 将当前模型Nash策略与先前研究的两阶段最优解进行比较，报告显示信息交易者的平均市值增长约4.5%，经纪人平均市值下降约5.5%，显著体现信息公开对市场参与者盈利分配的影响。

- 统计检验表明上述差异高度显著，强调了在信息透明市场中的交易者利益博弈特征。

• 结论强调此类模型对去中心化金融（DeFi）自动化做市商等场景的指导意义。

---

三、图表深度解读

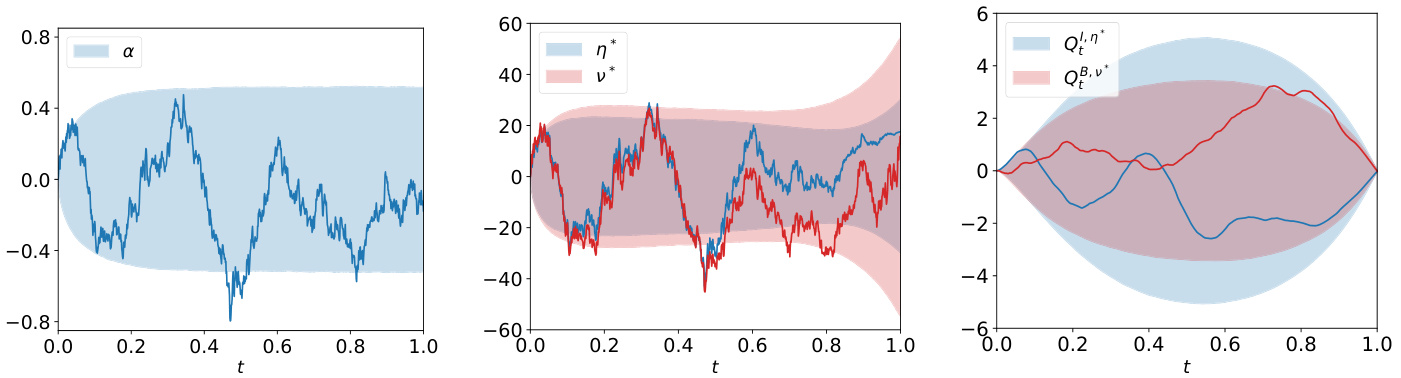
图1（第21页）

• 描述： 图1展示了模型中关键价格信号$\alpha$、信息交易者交易速度$\eta^$、经纪人交易速度$\nu^$以及两者对应的库存量$Q^{I,\eta^}$和$Q^{B,\nu^}$的单条样本路径及其5%和95%分位数区间。

- 数据趋势：
- $\alpha$作为交易信号，围绕零均值上下波动，体现OU过程特征。
- $\eta^$与$\alpha$走势高度相关，反映信息交易者利用信号进行趋势跟踪。
- 经纪人交易速度$\nu^$逻辑地以需对冲和投机为目标，活跃且与$\eta^$无完全同步。
- 库存量$Q^{I,\eta^}, Q^{B,\nu^*}$动态波动，但大体保持平稳，库存风险未出现剧烈失控。

• 文本联系： 支持作者关于交易策略结合价格信号和库存控制的论述。

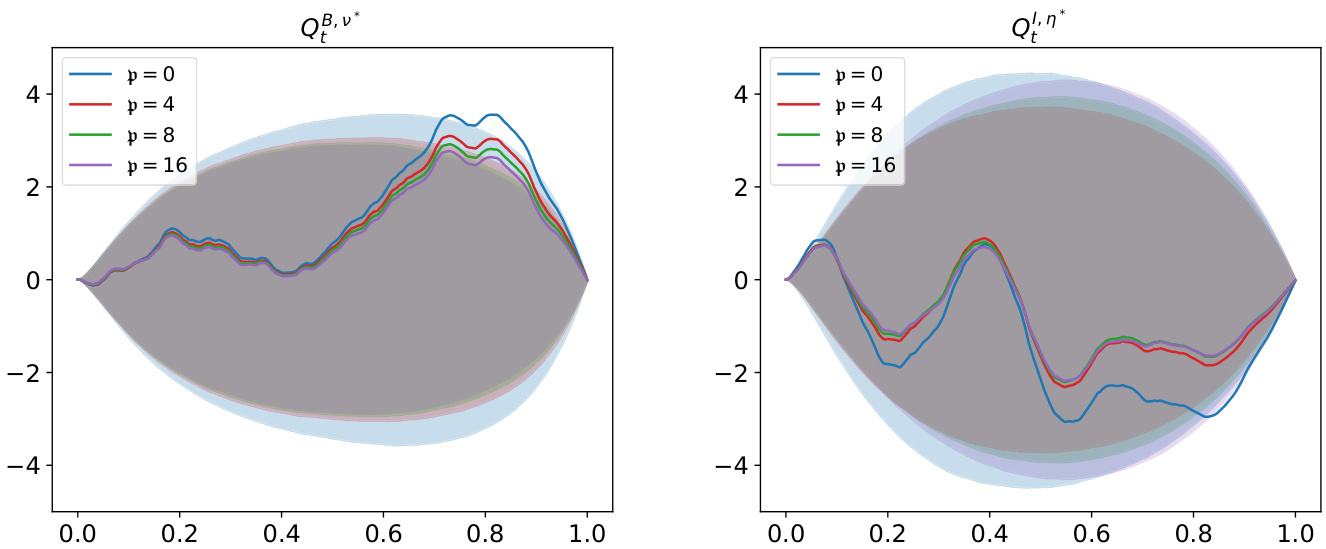
图2（第21页）

• 描述： 展示当转瞬即逝价格冲击衰减率$\mathfrak{p}$取4个不同值时，经纪人和信息交易者库存路径的样本仿真及其量化区间。

- 数据趋势：
- 经纪人库存的分布区间随着$\mathfrak{p}$增加变窄，表现为更好的库存管理能力。
- 信息交易者库存呈现非单调趋势，初期分布集中的同时末期扩散幅度加大，可能对应投机性增强。

• 文本联系： 支撑了瞬态价格冲击对参与者风险管理和交易强度的影响逻辑。

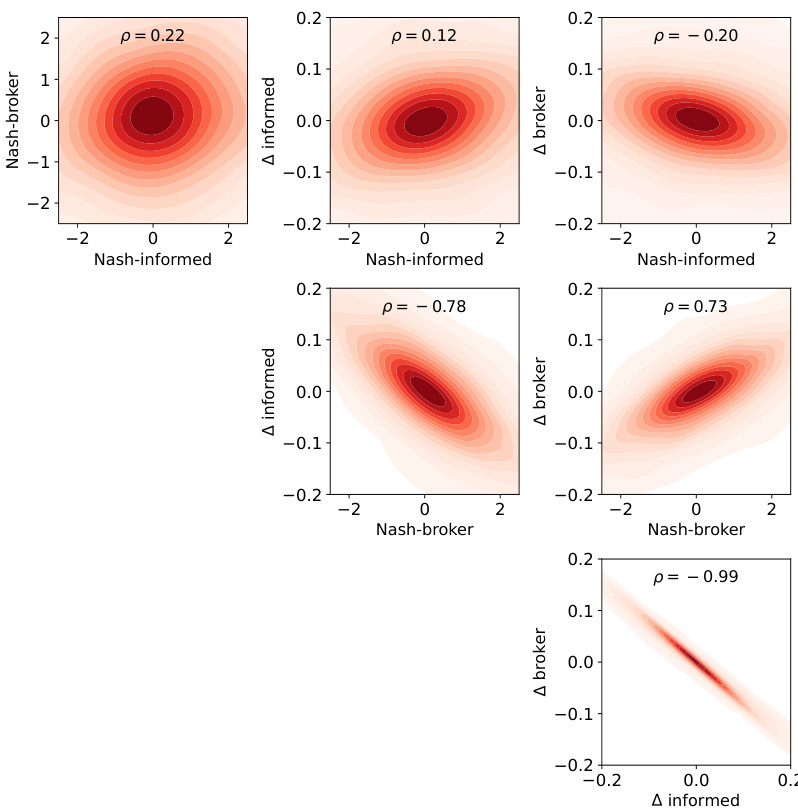
图3（第22页）

• 描述： 利用核密度估计的等高线图比较了本研究纳什均衡策略下与先前两阶段优化策略下经纪人与信息交易者的市值表现及其差异分布。包括相关系数统计。

- 数据趋势与解析：
- 正相关的均值分布表明两策略均表现出一定程度的经济相似性。
- 不同标的资产的差异散点显示了策略下的盈利重新分配，且统计检验显示该差异显著。
- 负相关系数对应利润迁移的零和特征。

• 文本联系： 用以佐证主题观点—信息公开时经纪人和消息交易者之间的利润重新分配机制。

---

四、估值分析

虽然报告核心不涉及传统意义上公司的估值，而是着重资产交易策略的纳什均衡，但在数学上可以理解为性能指标的最大化问题，本质上是收益-风险权衡的博弈均衡估计。其估值框架体现在：

• 收益函数： 结合了市场价格、库存成本及交易费用的期望终值。

- 优化方法： 通过SDE控制和FBSDE系统刻画，求解稳态收益及策略。

• Riccati方程角色： 作为二次性能指标下最优控制问题中标准的矩阵微分方程，体现均衡策略参数的动态权衡和反应。

- 敏感性隐含于参数选择： 如价格冲击强度${\mathfrak{h}}$，衰减率${\mathfrak{p}}$，库存惩罚系数$\phi,\psi,r^B,r^I$等，均直接影响解的稳定性及具体策略表现。

---

五、风险因素评估

报告直接讨论的风险主要围绕以下几点：

• 库存风险： 由库存成本惩罚系数控制，防止策略在实际交易中出现高风险敞口。

- 信息不对称： 模型核心之一，信息交易者利用私人信号，驱动非对称市场动态，导致毒性流动（toxic flow）风险。

• 交易冲击风险： 由于价格冲击模型包括瞬时与瞬态影响，交易行为对市场造成的价格波动可能引发额外风险。

- 模型参数及时间窗限制： 存在保证均衡解唯一性的技术条件，如交易时间长度$T$及冲击参数范围，若违反可能无法保证解的存在。

• 数据和模型假设风险： 如假定非信息交易者是随机流且独立于其他过程，实际市场可能更复杂。

报告中并无详细缓解策略，但通过合理设定库存惩罚和选择参数范围以保证系统稳定与效用函数凹性，间接减少风险。

---

六、批判性视角与细微差别

• 模型假设的限制： 假设非信息交易者行为为均值回复的随机过程，不参与策略性优化，可能低估复杂市场动态中的交易行为。

- 价格冲击模型： 采用指数衰减模型为经典但理想化，真实市场价格冲击可能呈现更加复杂的非线性和不对称特征。

• 视角侧重于完美信息纳什均衡，现实中往往信息不完全且噪声多，这些因素可能影响策略实际有效性。

- 计算复杂度： 尽管获得闭式解，但实际应用需要大量计算资源，特别是高频数据下的参数估计和策略优化。

• 文中部分公式文本有转录错误或排版混乱，需结合上下文和已有文献进行判断，确保理解准确。

---

七、结论性综合

本文通过建立一套基于前向-后向随机微分方程系统的动态博弈模型，深入研究了经纪人与不同类型交易者（信息交易者与非信息交易者）之间的战略互动，构造了一个包含瞬时与瞬态价格冲击以及库存风险控制的实用市场交易模型。模型核心成果包括：

• 纳什均衡策略存在解的严格数学证明，涵盖不同时空参数范围和价格冲击形态。

- 闭式解的构造连接了矩阵Riccati微分方程及线性BSDE，提升理论的透明度和计算效率。

• 数值模拟凸显了信息信号对市场参与者交易行为和库存策略的重大影响，体现了信息优势如何被经纪人捕捉和利用。

- 不同价格冲击衰减率对经纪人和信息交易者库存波动的显著影响，反映策略稳定性与风险容忍度的平衡。

• 与先前两阶段优化模型的绩效对比揭示了信息公开在策略间盈利重分配的效应，提示市场参与者在信息透明度提升时需重新评估其竞争优势。

报告中的图表直观展示了价格信号驱动下的交易速度与库存动态（图1），价格冲击衰减对库存路径分布的调节（图2），以及两种策略方案下市值差异及其统计相关特征（图3），有效辅助解释文中理论推断与模型结论。

综上，作者展示了一个高度严谨且数学深度丰富的交易策略分析框架，为理解经纪人与客户之间基于信息交互的最优交易行为提供了重要理论工具，对算法交易、市场微结构研究以及去中心化金融等领域均有显著参考价值。[page::0, page::1, page::2, page::3, page::5, page::6, page::7, page::8, page::9, page::10, page::11, page::12, page::13, page::14, page::15, page::16, page::17, page::18, page::19, page::20, page::21, page::22]

---

八、报告主要图表Markdown格式引用

• 图1：

• 图2：

• 图3：

报告