文章结构与研究问题 [page::0][page::1]

• 分析单一企业和两个企业在有无激励机制下的排放控制问题。

- 建立了包含脏技术和清洁技术的动态生产模型，考虑不确定性和竞争互动。

单企业模型与最优策略 [page::1][page::4][page::8]

• 企业通过动态控制技术投资率 $a=(a^{1},a^{2})$，旨在最大化风险厌恶型效用。

- 最优支付率 $z^$ 由 PDE 与矩阵 ODE 系统确定：
$$
z{i}^ = \frac{\gammai vi + \sigmai^2 \etap vi}{\sigmai^2 \etap + \gammai + \etaA \sigmai^2},\quad i=1,2
$$

• 价值函数拟合为二次形式，系数满足相关 ODE 系统。

双企业模型及激励机制 [page::2][page::4][page::8][page::9]

• 监管者设计激励支付变量 $Z$，解决包含两企业耦合随机控制问题。

- 激励下的支付率 $z^{11}, z^{12}$ 由解析公式给出，考虑了风险厌恶和协同影响：
$$
\begin{cases}
z{11}^ = \Lambda{12} v1,\quad z{12}^ = \frac{\etap}{\eta1 + \etap} (1 - \Lambda{21}) v2 = \frac{\eta2 \etap \sigma2^2}{(\eta1 + \etap)(\gamma2 + (\eta2 + \bar{\eta}1)\sigma2^2)} v2 \\
\Lambda{12} = \frac{\gamma1 + \bar{\eta}2 \sigma1^2}{\gamma1 + (\eta1 + \bar{\eta}2)\sigma1^2},\quad \Lambda{21} = \frac{\gamma2 + \bar{\eta}1 \sigma2^2}{\gamma2 + (\eta2 + \bar{\eta}1)\sigma2^2}
\end{cases}
$$

• 相应的 PDE 转化为带有非线性项的矩阵微分方程。

无激励下企业博弈均衡分析 [page::2][page::3][page::10][page::11][page::12]

• 模型视为二人微分博弈，寻找反馈形式的纳什均衡 $(\hat{a}^1, \hat{a}^2)$。

- 双方价值函数均采用指数效用，构造二次型值函数，系数满足耦合非线性ODE系统。

• 回测和数值示例揭示均衡策略受竞争策略影响显著，存在市场失灵风险。

主要参数设定及数值实验 [page::5][page::7]

| 参数 | 取值 |
|------------|---------|
| $\sigma1$ | 0.2 |
| $\sigma2$ | 0.3 |
| $p0$ | 1.0 |
| $p1$ | 0.6 |
| $p2$ | 0.4 |
| $\eta1$ | 1.0 |
| $\eta2$ | 1.0 |
| $\gamma1$ | 1.5 |
| $\gamma_2$ | 1.0 |

• 数值结果显示企业的最优激励和竞争策略呈现良好的动力学变化趋势。 [page::5][page::7]

结论总结 [page::6][page::8]

• 随机控制方法有效捕捉了能源低碳转型中的投资与生产策略优化。

- 竞争降低去碳化效率，监管激励机制能明显提升清洁技术采纳率。

• 强调设计合理监管工具对市场低碳转型的重要性，建议未来扩展模型复杂度。 [page::6][page::8]

报告深度分析：《Optimal Incentive for Regulated Production》

---

1. 元数据与报告概览

• 标题：Optimal Incentive for Regulated Production

- 作者：Benhao Du, Thomas Treillard, Francois Wang

• 机构与发布日期：未明确具体机构，日期为2025年6月18日

- 主题领域：能源市场的去碳化策略与激励机制，利用随机控制模型分析能源生产企业对清洁技术的投资及生产决策。

• 关键词：随机控制、能源市场、Hamilton-Jacobi-Bellman方程（HJB）、偏微分方程（PDE）。

- 核心论点：论文通过构建三类递进式复杂度的随机控制模型，首次分别在单个企业、两个企业（含监管激励）、和两个企业（无激励）场景下，系统分析了企业在不确定环境中生产和投资清洁技术的最优策略。强调了激励机制在推动去碳化转型中的关键作用，同时揭示竞争环境下的战略互动会导致去碳化程度的低效。

本报告的目标是为设计更有效的监管激励机制提供理论依据，量化竞争与监管力量对企业清洁技术投资决策的影响。[page::0,1]

---

2. 逐节深度解读

2.1 引言（Introduction）

• 介绍了低碳经济转型的挑战和能源企业在清洁与污染技术间权衡的复杂性，强调在有不确定性的市场下理解企业行为对设计有效监管框架至关重要。[page::0]

2.2 模型构建（Model）

2.2.1 单一企业模型

• 企业控制两个技术状态变量 \( X^1, X^2 \)，分别代表污染技术与清洁技术的生产水平，状态演化由以下随机微分方程控制：

\[
dXt^i = at^i dt + \sigmai dWt^i, \quad i=1,2,
\]

其中 \(at^i\) 是企业的控制速率，\(W^i\)是标准布朗运动。

• 成本函数为控制力度的二次函数形式：

\[
c(a) = \frac{1}{2}\frac{a1^2}{\gamma1} + \frac{1}{2}\frac{a2^2}{\gamma2},
\]

体现调整生产技术的边际成本递增。

• 收益函数基于两技术产出水平与市场价格的线性函数：

\[
f(x) = (p0 - p1 x1 + p2 x2)(x1 + x2),
\]

结合了价格与产量的影响。

• 企业目标为最大化期望效用：

\[
JA = \mathbb{E}\left[ UA \left( YT - \int0^T (f(Xt) - c(at)) dt \right) \right],
\]

其中 \( YT \) 为支付给监管者的激励或罚款。监管者则通过控制 \(Zt\) 优化自己的效用，解耦两个控制变量（企业激励率）。模型形式细致体现了企业与监管者间的动态博弈。

• 假设各技术控制互不影响，转换为一个带有Hamilton-Jacobi-Bellman (HJB) PDE的最优控制问题，目标是解确定激励支付结构 \(z^\) ，使得企业达成最优清洁技术投资和生产分配策略。[page::1]

2.2.2 双企业模型

• 两个企业分别拥有各自的技术状态变量和控制权，状态动态与单企业类似，但竞合关系更复杂。
• 监管者同样设计激励方案，用于影响两企业的生产与投资行为，以实现社会最优目标。
• 总支付 \( YT = YT^1 + YT^2 \) 的计量模型明确引入了两个企业间的交叉影响项 \(Zt^{i,j}\)，反映了一个企业控制行动对另一企业的影响（如技术溢出或市场竞争）。
• 成本函数和收益函数延续单企业结构，同时引入新的奖励函数 \(R(z)\) 考虑随机波动和企业策略交互的风险。
• 监管问题依旧转化为非线性偏微分方程，目标是最大化社会整体期望效用。该模型框架刻画了有激励机制时企业动态之间的复杂互动。[page::2]

2.2.3 无激励的企业战略均衡

• 考察当监管者未施加任何激励时，两企业如何在市场中竞争。
• 明确列出各企业的控制变量 (\(at^i\)) 为碳排放减少努力，状态动态为带噪声的排放演进。
• 成本结构为二次型，收益函数体现价格下降及排放量对收益影响。
• 企业目标是最大化各自的风险厌恶型期望功效函数，形式为负指数效用函数。
• 通过构造纳什均衡的定义，求解双方最优反应函数，构建反馈策略对。
• 状态变量与行动一同构成一个非合作的动态随机博弈环境，意在揭示无监管时竞争导致的清洁技术投资缺乏与市场失败问题。[page::2,3]

---

2.3 结果分析（Results）

3.1 单企业两技术的最优控制

• 关键结论：最优激励支付率 \(z^ = (z1^, z2^)\) 具有解析形式：

\[
zi^ = \frac{\gammai vi + \sigmai^2 \etap vi}{\sigmai^2 \etap + \gammai + \etaA \sigmai^2},
\]

其中 \(v\) 是扩展的价值函数，带有二次形式参数 \(A, B, C\)，它们满足一组主线性矩阵ODE。

• 此结果表明激励结构与系统的风险厌恶参数 \(\etap, \etaA\)、波动率 \(\sigmai\) 与成本参数 \(\gammai\)紧密相关。
• ODE系统代表价值函数随时间衰减动态，直接决定了生产投资策略的时间路径。[page::4]

3.2 双企业模型下的激励

• 激励支付率 \(z^{11}, z^{12}\) 由复杂比率 \(\Lambda{ij}\) 及风险厌恶参数等表达：

\[
z{11}^ = \Lambda{12} v1, \quad z{12}^ = \frac{\etap}{\eta1 + \etap} (1 - \Lambda{21}) v2 = \frac{\eta2 \etap \sigma2^2}{(\eta1 + \etap)(\gamma2 + (\eta2 + \bar{\eta}1) \sigma2^2)} v2,
\]

同时 \(\Lambda{12}, \Lambda{21}\) 定义了两个企业间激励的权衡关系。

• 价值函数依旧为二次形式，满足对应的矩阵微分方程，用数值方法求解。
• 表明监管激励机制应考虑竞争双方的风险偏好特性与成本参数，设计差异化激励以引导均衡向高质量去碳转型。[page::4,9]

3.3 无激励均衡策略

• 对于给定竞争对手确定策略，发挥单企业最优控制工具，得到反馈控制律：

\[
at^{i,} = - \frac{\gammai \partial{xi} vi}{\etai vi},
\]

其中 \(vi\) 是企业i的价值函数，假定为指数负效用，\(Wi\)为对应的二次形式函数，参数满足复杂ODE系统。

• 系数ODE系统包含方差、风险厌恶、价格参数与对手控制路径，数值解表明对手策略强烈影响本企业控制参数（尤其线性项 \(D(t), E(t)\)），从而影响清洁技术的投资力度。
• 进一步通过正向求解两企业交互的耦合ODE系统确认纳什均衡的存在及其特性。由于拥挤的非线性结构，实际依赖数值方法实现（见图2）[page::5,6,7]

---

3. 图表深度解读

图1（第5页）

• 描述：展示Firm 1的系数 \(A(t), B(t), C(t), D(t), E(t), F(t)\) 随时间的演变，各图对应Firm 2采取的三个不同常值策略 \(a = -1, 0, 1\)。
• 解读：

- 随着竞争对手策略变动，指标 \(D(t), E(t)\) 明显变化，表明这些线性项对对手的清洁技术投资敏感。

- 系数 \(A(t), C(t), B(t)\) 变化体现了二次项权重调整，影响到Firm 1对自身碳排放与交叉效应的重视程度。

• 关联文本：支持了竞争策略不可忽视的反馈效应，显示出竞争对手的行动直接影响单企业的最优减排行动，确认了模型中战略互动的重要性。[page::5]

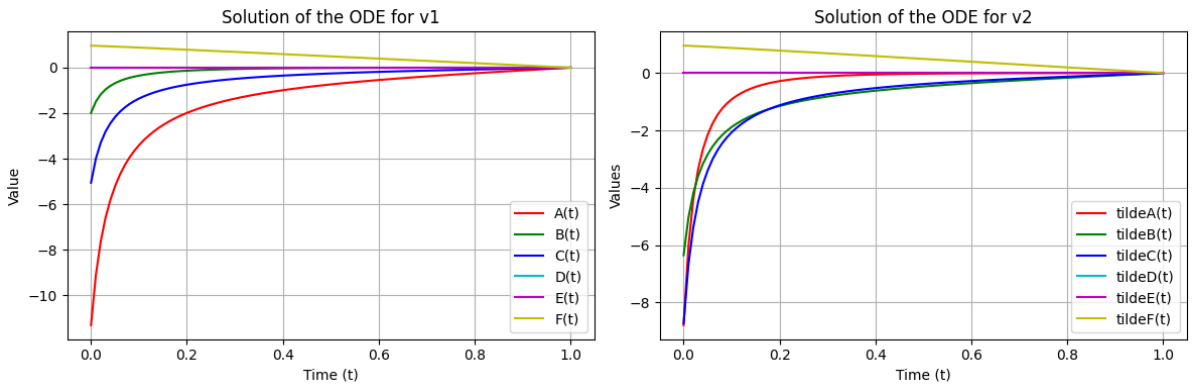
图2（第7页）

• 描述：耦合ODE系统的数值解，用以描述两个企业的价值函数分量变化，分别对应 \(v1\) 与 \(v_2\) 的二次项系数，显示动态纳什均衡的时间演化。
• 解读：

- 各系数均从负值逐渐趋向于终点0，体现时间截点终端条件的满足。

- 系数间的差异揭示了两企业风险偏好及成本异质性对均衡路径的影响。

• 关联文本：数值例证支持理论推导的均衡特征，强调求解此类复杂非线性系统需借助高效数值方法。[page::7]

---

4. 估值分析

• 报告核心不是传统企业估值，而是对生产控制与投资策略的最优控制问题进行价值函数求解，价值函数表达了动态最优期望效用。
• 采用HJB偏微分方程框架，将随机控制问题转化为求解相关矩阵微分方程（ODE）。
• 在单企业和双企业模型中，价值函数采用二次型假设 \( v(t,x) = \frac{1}{2} x' A(t) x + B(t) x + C(t) \)，将PDE归纳为矩阵ODE组。
• 通过批准赛和变量替换，求得显式或半显式的激励率表达式，对应不同风险参数、波动率和成本。
• 敏感性体现在风险厌恶参数、技术波动率和成本参数对激励结构的效果显著影响，直接影响对清洁技术的投资倾向。
• 在无激励情形，求纳什均衡对应的是两个企业价值函数的耦合HJB方程，解的复杂性提升，需要结合数值方法预测均衡路径。[page::4,8,9,10]

---

5. 风险因素评估

• 报告明确考虑了以下风险：

- 市场需求和价格不确定性：采用随机布朗运动模型模拟技术演进与市场波动。

- 风险厌恶参数差异：不同企业对利润波动的风险承受能力不同，影响其投资决策。

- 战略行为风险：竞争对手行动不可预测导致投资调整风险。

- 激励设计风险：监管激励方案可能设计不当，导致企业行为未能达成社会优化。

• 潜在影响：

- 竞合关系中，竞争可能导致“搭便车”行为，降低整体去碳效率。

- 激励不足或未针对性设计时，企业动机不足，去碳转型延迟。

• 报告指出引入监管激励便可缓和竞争导致的市场失灵，是有效降低风险的一种策略，但未详细提出具体缓解方案，是未来研究方向之一。[page::1,2,6,8]

---

6. 批判性视角与细微差别

• 模型假设简化：二次成本函数与指数效用函数虽常用，但现实中成本结构可能更复杂，且多种不确定因素（政治风险、技术路径依赖）未涵盖。
• 竞争模型局限：双企业模型为静态数量，两者策略多为反馈型，缺少动态学习、异质性企业规模和非对称信息的影响。
• 激励设计简化：激励方案局限于线性支付规则，现实监管通常更加复杂多变（混合税收、补贴、配额等）。
• 数学表达复杂：耦合ODE系统部分章节（第6页部分）展现公式错误或排版异常，可能降低理解精度。
• 数值例子有限：参数选择固定，缺少灵敏度分析，难以全面评估政策建议在不同市场环境中的适用性。
• 政策适用建议：结论指向加强监管激励，但缺乏对实际政策设计细节、动态演化与合规成本的考量。

---

7. 结论性综合

本报告通过严谨的随机控制理论和HJB偏微分方程框架，系统建模评析了能源生产企业的去碳化投资策略，特别针对监管激励和竞争行为的复杂互动。以单企业、双企业激励机制及无激励纳什均衡三个层次，详细展现了最优控制策略及价值函数的数学特征，得出以下关键发现：

• 激励机制显著提升清洁技术投资意愿，通过明确激励支付率表达式，链接风险、成本和市场波动参数，指导政策制定者设计合理的监管方案。
• 竞争环境下缺乏激励导致市场失灵，战略行为阻碍社会最优去碳结果，支持引入有效激励以纠正市场不完善。
• 数学架构严谨，PDE-ODE系统的求解构成企业家行为动态的理论基础，数值图表清楚展示战略互动对控制参数的影响，凸显竞争对手行为对企业自我调节的重要性。
• 模型在风险厌恶和技术波动的定量影响上提供明确洞察，助力评估不同市场和企业特征下的政策效果。

综上，报告为能源市场去碳化的理论研究提供了坚实的数学支持和策略参考，揭示了监管激励设计的核心机制及市场竞争的结构性障碍，具有较强的学术和政策指导价值。[page::0-12]

---

重要图表展示

图1：Firm 1在不同Firm 2策略下的ODE系数变化

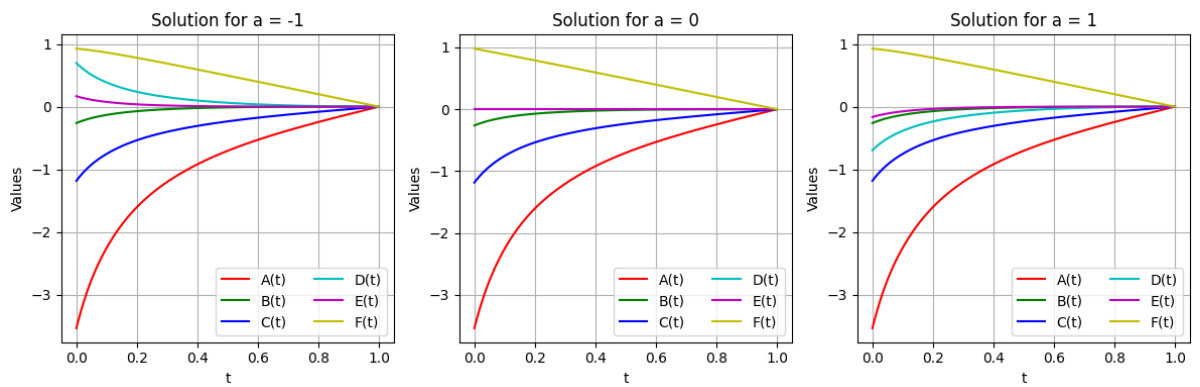
图2：双企业耦合ODE数值求解

---

术语及概念说明

• 随机控制（Stochastic Control）：解决在随机环境下，如何选择控制策略以优化某一性能指标的数学方法。
• Hamilton-Jacobi-Bellman方程（HJB）：描述最优控制问题的偏微分方程，价值函数满足该方程。
• 价值函数（Value Function）：在动态优化中代表某一时刻状态下可达到的最大期望效用。
• 纳什均衡（Nash Equilibrium）：在竞争环境中，所有参与者都无法通过单方面改变策略获得更好结果的策略组合。
• 风险厌恶效用函数：用负指数函数刻画决策者对风险的敏感度，值域与风险偏好相关。
• 激励支付率（Incentive Payment Rate）：监管者给予企业的奖励或惩罚额度，引导企业行为。
• 反馈控制策略：控制值依赖于当前状态的策略，而非预先设定的时间序列。

---

综上所述，该报告具有全面的模型构建、理论推导和数值分析框架，是深入理解能源市场去碳化政策设计的宝贵资料。

报告