神经常微分方程（Neural ODE）模型解析 [page::2][page::3]

• 传统ResNet模型的离散残差结构被连续化表示为ODE-Net，通过求解神经常微分方程统一表达网络隐藏状态演变。

- 伴随灵敏度方法实现ODE-Net的反向传播，优化参数更新，节省内存但略牺牲精度。

• MNIST数据集测试显示ODE-Net在相似测试误差下，参数量和内存消耗均低于ResNet。

液态神经网络（Liquid Neural Networks）核心结构 [page::4][page::5][page::6][page::7][page::8]

• LTC网络基于生物神经元电位动态建模，采用半隐式欧拉法数值求解，显著增强模型表达能力和稳定性。

- NCP网络继承LTC结构并引入稀疏化及分层网络设计，灵感源自线虫神经系统，减少可训练参数，提升稳健性和可解释性。

• NCP具有抗噪声能力，在自动驾驶等任务中表现优异，参数规模显著小于传统RNN、LSTM模型。

闭式连续时间神经网络（CFC）设计与优势 [page::11][page::12][page::13]

• 通过推导LTC微分方程的近似闭式解，CFC避免了复杂的微分方程求解过程，极大提升计算效率。

- 采用门控机制控制记忆保留，提升模型灵活性和表达能力。

• CFC在人类活动识别任务中达到最高准确率且训练速度最快。

液态神经网络在量化选股中的实证对比 [page::14][page::15][page::20][page::21]

| 模型 | RankIC均值 | RankIC胜率 | 多头年化收益率 | 多空年化收益率 | 所需显存 |
|-------------|------------|------------|----------------|----------------|----------|
| GRU | 12.8% | 87.1% | 24.2% | 65.6% | 120Gb |
| LTC | 12.5% | 88.2% | 22.2% | 58.9% | 80Gb |
| NCP (LTC) | 13.4% | 87.2% | 24.4% | 62.4% | 80Gb |
| CFC | 13.1% | 87.2% | 23.2% | 60.8% | 6Gb |
| NCP (CFC) | 12.3% | 88.1% | 23.7% | 62.7% | 6Gb |

• 液态神经网络与GRU因子相关性在0.69至0.82之间，说明不同模型学习到不同价量特征。

- 在分年度和样本外回测中，液态神经网络尤其是NCP结构表现稳定且通常优于传统GRU。

• 通过显著降低显存需求（CFC/NCP仅为GRU的5%），提升了大数据量和有限资源环境下的训练可能性。

稳健性与可解释性优势 [page::9][page::10][page::13]

• NCP和CFC网络在面对输入噪声时表现出显著更强的稳健能力，适用于异常变化频繁的股票数据特征环境。

- NCP模型具有更少神经元和稀疏结构，使得每个神经元的动态行为更易于分析和解释。

• 注意力图显示液态神经网络在关键特征上聚焦能力优于传统模型，有助于量化策略的环境适应性理解。

【广发金工】神经常微分方程与液态神经网络 — 详尽分析报告

---

1. 元数据与概览

• 报告标题：《神经常微分方程与液态神经网络》

- 作者与联系方式：安宁宁（广发证券首席金工分析师）、陈原文（资深金工分析师）、林涛（研究员）

• 发布机构：广发证券金融工程研究团队

- 发布日期：2025年3月6日

• 研究主题：机器学习领域前沿模型“神经常微分方程”与“液态神经网络”的技术原理解析及在量化选股中的实证效果评估。

- 核心信息：
- 报告重点介绍了基于微分方程形式的连续时间神经网络模型，包括神经常微分方程网络（ODE-Net）、液态时间常数网络（LTC）、神经电路策略网络（NCP）与闭式连续时间神经网络（CFC）。
- 这些模型将传统的离散时间循环神经网络“连续化”，带来更强表征能力、稳健性和计算效率。
- 实证部分将这些模型与传统GRU循环神经网络在真实市场选股策略中的表现进行对比，发现液态网络能够在显存和计算效率方面显著优于GRU，且表现相当，NCP结构尤为出色。

简而言之，作者旨在传达神经常微分方程及其衍生的液态神经网络在量化选股策略领域具有广阔前景，通过提升模型效率和稳健性，有望替代传统循环神经网络方案。[page::0,1,13,20]

---

2. 逐节深度解读

2.1 神经常微分方程（NN-ODE）

• 背景介绍

ResNet通过残差连接解决深度网络训练难题，其残差结构为 $h{t+1} = f(ht, \thetat) + ht$。NeurIPS 2018年Chen等提出，将无限堆叠的残差块参数统一视为常微分方程的求解变量，进而提出“神经常微分方程”模型（ODE-Net），即用微分方程表征层间连接关系：
$$ \frac{d h(t)}{d t} = f(h(t), t, \theta) $$

• 基本逻辑与方法

- 求解该ODE可取得连续时间的隐藏状态表示，无需显式递推所有层的参数。
- 伴随灵敏度方法（Adjoint Sensitivity Method）被用来实现反向传播，降低内存消耗但代价是反向传播精度有所牺牲。

• 关键数据及性能表现

表1显示，ODE-Net与ResNet在MNIST上相似的测试误差水平下，参数量和显存占用明显减少（如ODE-Net内存为$O(1)$，而ResNet为$O(L)$，其中L为层数），体现模型在复杂度和资源利用上的优势。[page::2,3]

• 图表解析

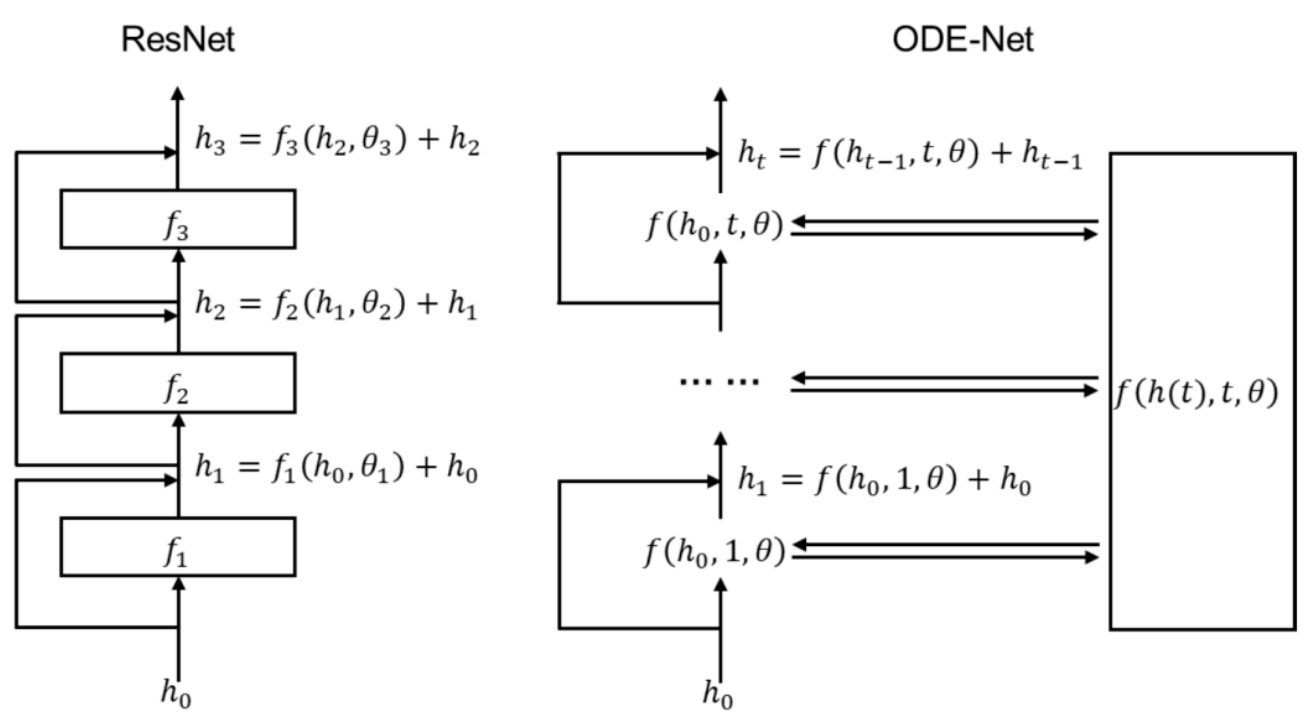
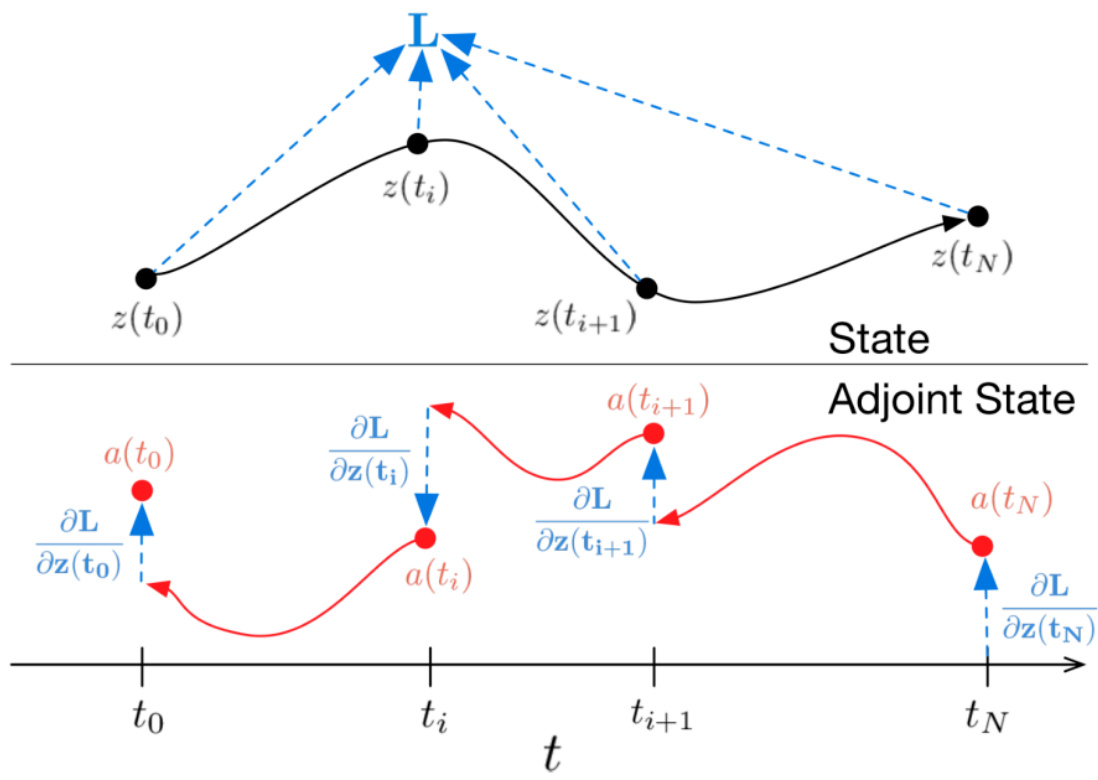
图1对比了ResNet与ODE-Net结构，直观展示了动态从离散残差块跳跃到连续微分表示的概念，强化了理论意义。图2细致阐释了反向传播计算动态，并配合表1验证理论效率。[page::2,3]



---

2.2 循环神经网络（RNN）与液态神经网络

• 传统RNN模型回顾

RNN利用时间步离散序列输入，隐藏状态随步长递推（$ht = f(xt, h{t-1}, \theta)$），捕捉序列动态特征，广泛用于量化选股。

• 液态神经网络的创新

将传统RNN的离散状态更新“连续化”，处理隐藏状态的微分变化率而非差分。
代表性模型：
- LTC（Liquid Time-constant Networks）
- NCP（Neural Circuit Policies）
- CFC（Closed-form Continuous-time Networks）

• LTC模型核心

LTC隐含生物学灵感，模型中每个隐藏神经元的状态被微分方程控制：
$$ \frac{d hk(t)}{d t} = -\frac{h_k(t)}{\tau} + S(t) $$
$S(t)$ 表示突触电流，激活输入提供非线性建模能力，$\tau$为时间常数表达衰减速率。采用半隐式欧拉步法求解该ODE，平衡速度与稳定性，使用梯度反向传播更新参数。实验显示LTC在多个时间序列任务上的性能较LSTM、GRU提升5%~70%[page::4,5].

• NCP模型特点

NCP灵感来源于线虫神经系统，采用分层稀疏结构代替LTC的全连接。神经元有明确不同功能分工，连接稀疏且参数少，增强了模型稳定性和可解释性。
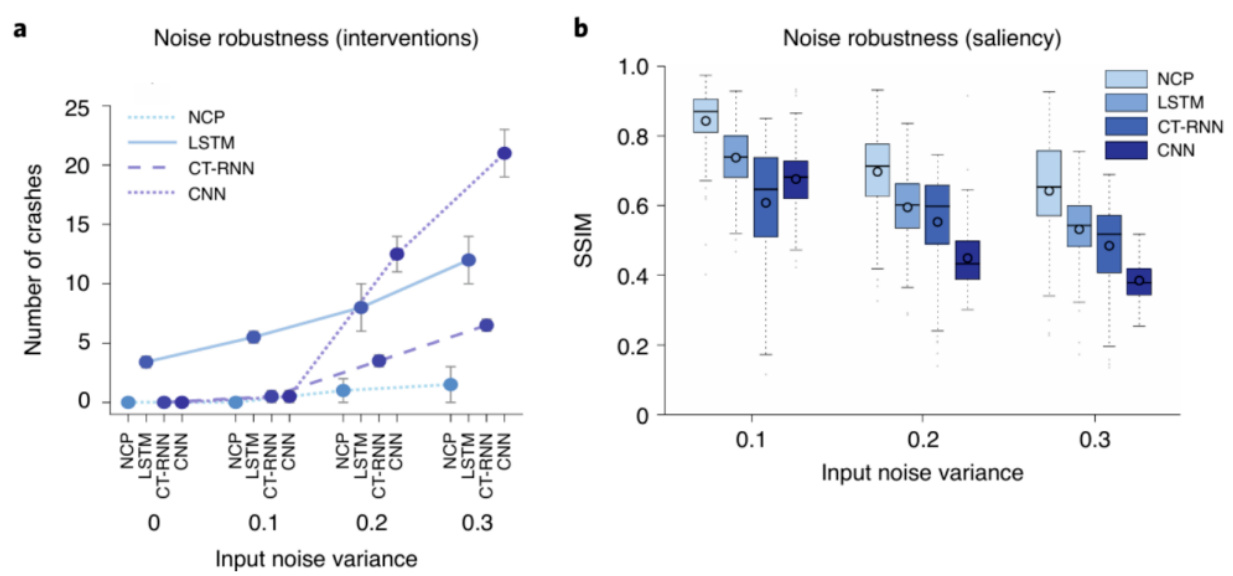
具备强抗噪声能力，尤其在自动驾驶任务场景中，测试时不同噪声水平下维持较低碰撞率和更好的图像注意力表现。相比LSTM、标准RNN，NCP呈现更小的模型误差与训练参数量[page::7,8,9,10].

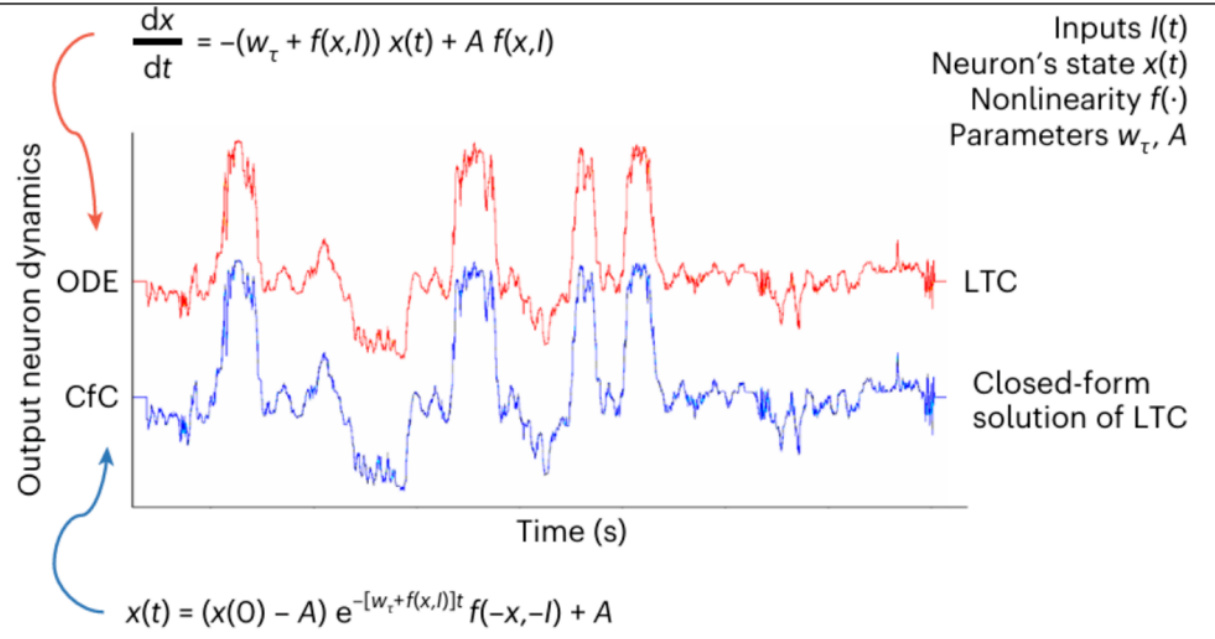
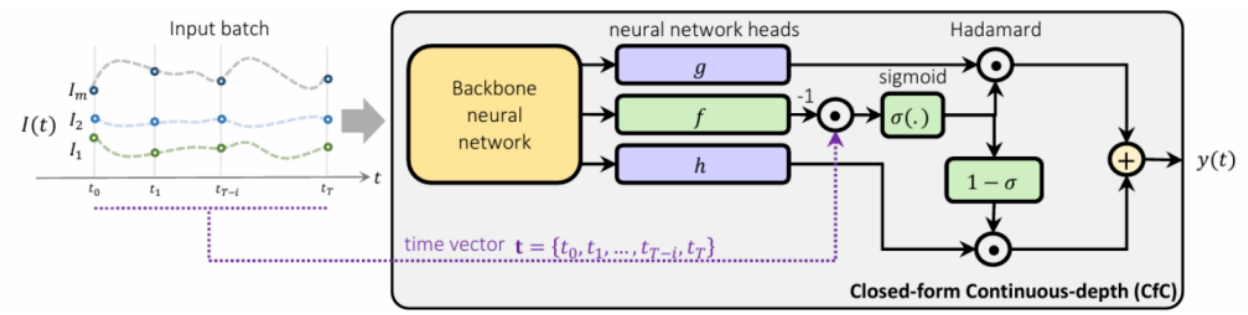
• CFC模型亮点

针对LTC需数值求解微分方程导致计算代价高昂，CFC提出LTC微分方程的近似闭式解。
此闭式解降低了计算复杂度同时保持较强模型表达力，并通过门控机制引入记忆保持能力。
该模型在多任务中测试，展示最快的训练速度与良好的准确性，稳健性亦与NCP类似[page::11,12,13]。




---

2.3 实证分析：液态神经网络在量化选股的表现

• 研究设计

在统一输入数据、目标函数及非主干结构的条件下，分别训练传统GRU与四个液态神经网络（LTC、NCP(LTC)、CFC、NCP(CFC)），对比其因子表现和回测收益。

• 数据说明

- 市场范围：全A股
- 时间区间：训练(2008-2016), 验证(2017-2019), 回测(2020-2024)
- 回测买卖策略遵循20交易日调仓，扣除千分之三交易成本
- 分组为10等份，并计算年化收益、最大回撤、夏普比率等指标[page::14]

• 整体表现

- RankIC和收益率方面，液态神经网络与GRU表现相当，无显著优势或劣势。
- 显存消耗方面，液态神经网络（特别是CFC和NCP(CFC)）显著节省，所需显存仅为传统GRU的5%左右（6Gb vs 120Gb），极大降低了训练资源压力。
- 因子相关系数显示，模型间的因子不完全一致，相关度大约0.69至0.82，说明不同主干网络学习到一定差异的因子特征[page::14]

• 分年度表现

详细年化收益率表明，NCP结构（尤其NCP(LTC)）在多个年度表现更优，夏普比率在顶尖模型中居前。
传统GRU的优势在于部分年度的多头收益稍高，但液态网络多空收益稳定且夏普表现优秀。
各模型均显著超越基准中证全指收益水平。
通过图15-24及表6-10的回测数据，液态网络因其网络稀疏和连续时间特性，能够保持较好稳定性和收益率，同时大幅降低显存和计算负担[page::15-20]。

---

3. 图表深度解读

• 图1（ResNet与ODE-Net结构对比）展示了经典ResNet通过离散层级实现的残差连接，和ODE-Net通过ODE连续描述状态演化的区别，说明神经网络未来可“连续化”，减少层数求解的复杂度。

- 图2描述伴随灵敏度方法反向传播的机制，展现神经常微分方程训练的关键数学工具。

• 表1比较传统层网络与ODE-Net的测试误差和参数，验证ODE-Net能用更小内存和参数，实现近似性能。

- 图4（LTC神经元示意）用生物学神经元图示形象说明LTC模型借鉴的生物电位动力学。

• 表2比较LTC参数更新的直接梯度反向传播与伴随方法，表明梯度法更准确，代价是更多内存。

- 表3展示LTC模型在多个时间序列任务中表现，明显优于传统RNN变种。

• 图5-7通过自动驾驶和简单RNN模型图说明NCP的架构及其基于生物神经系统的稀疏连接，强调结构紧凑、功能分工明晰。

- 图8通过碰撞数量和图像保持度两图呈现NCP在噪声鲁棒性上的优势。

• 图9-10NCP在自动驾驶测试中的平方误差和参数数量对比，证明精度与模型体积的双优。

- 图11展示CFC模型基于LTC微分方程的闭式解与原模型求解器轨迹的一致性。

• 图13CFC在活动识别任务上时间效率与准确率的对比表明闭式模型显著提升训练效率。

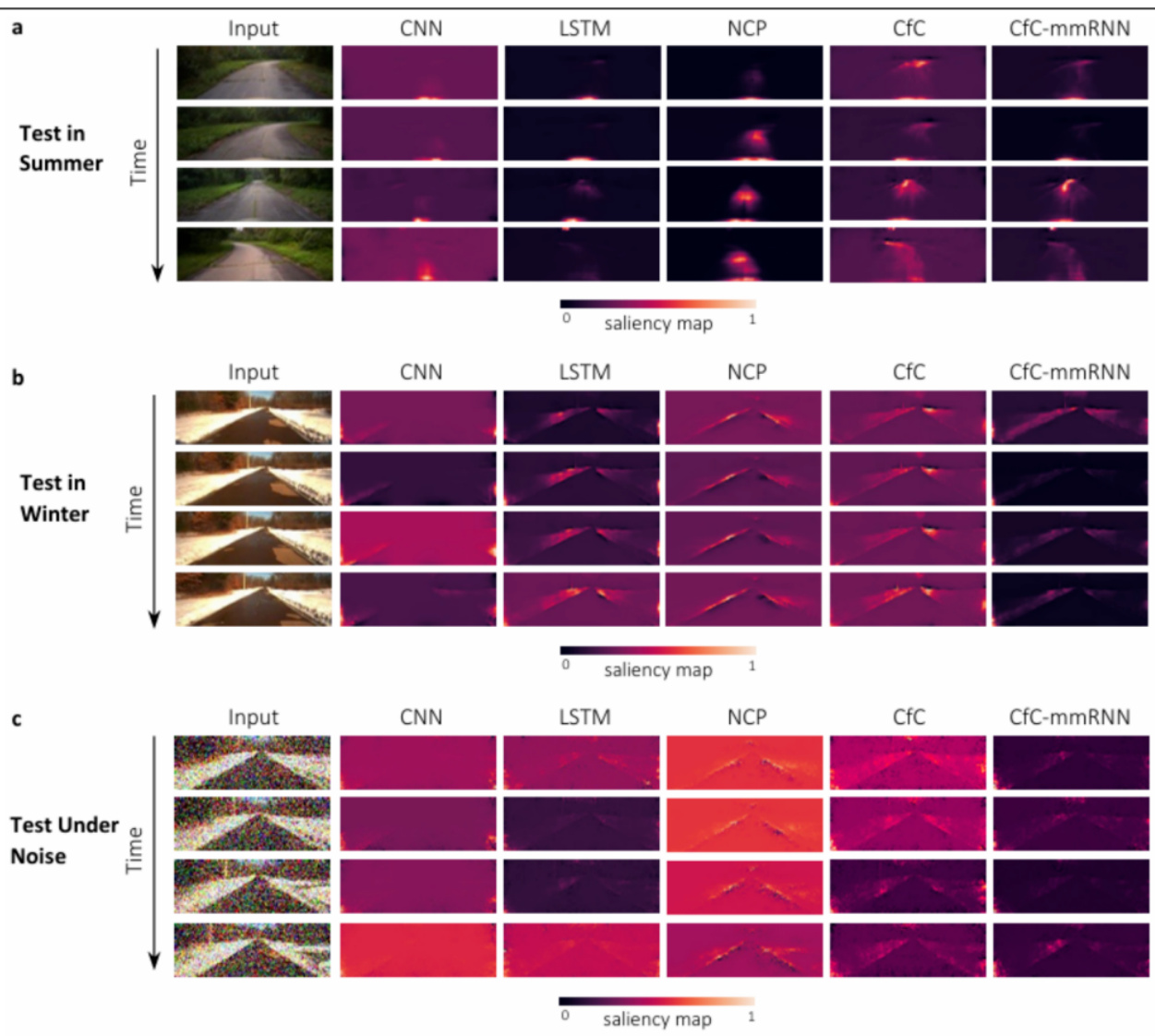
- 图14CFC对自动驾驶图像的注意力热图，在不同天气和噪声环境中表现出持续的车道识别能力。

• 表4-5GRU与液态网络整体显存使用与因子相关度表格。

- 图15-24及表6-10多头十分档收益、RankIC表现和年度回测统计全方位展示模型比拼，验证液态网络收益与风险特征整体优异或相近。

以上所有图表和数据共同构建了理论证明和实证验证的严密框架，支撑液态神经网络的创新价值与实操可行性。[page::2-3,5-6,7-10,11-14,15-20]

---

4. 估值分析

本报告核心为模型技术研究及实证回测，未包含传统意义上的金融资产估值方法（如DCF、市盈率等）。其“估值”层面集中体现在模型性能评价维度：

• 计算资源估值：显存与训练时间作为资源成本，液态神经网络相对GRU节约高达95%显存。

- 策略表现估值：基于RankIC、年化收益率、夏普比率、多空组合表现整体衡量量化因子及模型策略的相对价值。

模型的“价值”即在资源效率与投资回报之间寻求最佳平衡，液态神经网络展示了较为理想的计算/性能比，因而被视为提升量化投资模型“估值”的新方向。[page::2-3,12,14-20]

---

5. 风险因素评估

报告明确提出以下风险点：

• 模型风险：基于历史数据训练的模型方法固有数据驱动局限性，未来政策变动、市场环境、结构调整可能导致模型回测有效性失效。

- 市场风险：市场结构及交易行为变化，可能使基于历史统计规律构建的策略失效。

• 模型异同风险：不同量化模型之间存在基本假设和实现差异，观点和结果可能不一致。

报告未具体量化风险发生概率，也未给出详尽缓解措施，但提醒投资者应关注外部环境对模型适用性的动态影响及模型升级风险。[page::1,21]

---

6. 审慎与细微差别视角

• 报告作者主要依赖近年来顶刊成果和团队自我实证验证，体现较高的专业素养。

- 但液态神经网络因相对较新且较为复杂，训练与调参过程潜在非完全公开，可能存在模型过拟合时序数据或对特定任务表现优越但泛化性不足的问题。

• 伴随灵敏度方法与梯度反向传播各有优劣，报告中梯度法虽精确度高但对计算资源要求较大，实际应用中可能有折中考量不足。

- 实证对比始终建立在有限的市场历史中，且重点放于显存消耗等技术层面，缺乏对模型在极端市场环境或系统性黑天鹅事件中的抗风险性深入探讨。

• 对多个模型的具体实现细节和调参策略甚少披露，影响受众对模型可复制性和实现难度的判断。

总体而言，报告立场严谨，尽量避免夸大，但因应用新兴技术，存在技术路径尚未业内形成完全共识的自然限制。[page::1,21]

---

7. 结论性综合

本报告系统梳理了基于神经常微分方程的多种液态神经网络模型（ODE-Net、LTC、NCP、CFC）的理论构建、生物学灵感及连续时间建模优势，并详细分析了它们在量化选股中的应用表现。

• 理论突破：将传统离散递推的循环神经网络连续化，用微分方程描述隐藏状态动态。在数学基础和生物神经科学启发下，液态神经网络提供比传统循环网络更强的表达力和模型稳健性。

- 技术优势：半隐式欧拉法求解器及闭式近似解显著提升模型稳定性及计算效率。NCP结构稀疏且可解释性强，具备更优抗噪能力。

• 实证表现：四种液态神经网络模型相较于GRU，在股市量化选股策略中展示了相近年来整体不逊色的因子效力和收益表现。尤其是显存依赖显著降低（最低至5%），这为资源有限的量化策略开发和大规模模型训练打开新空间。

- 模型差异：因子相关度在0.69-0.82，指示不同模型捕捉了多样化的价格与成交量信息特征，为组合多元化投资提供潜力。

• 风险：市场结构变化及策略过度适配历史样本可能带来失效风险，需持续监控。

综上，液态神经网络兼具理论创新与实践价值，有望推动量化投资核心模型的迭代升级。NCP模型表现突出，可视为该领域的重点关注方向。CFC模型的计算效率优势也为高频交易和实时决策奠定基础。研究具备前瞻性价值，值得投资者和研究者长期关注和深入探索。[page::0~21]

---

参考摘录的关键表格与图示

| 表格/图号 | 内容描述 |
| --------- | -------- |
| 表1 | ODE-Net与传统卷积网络在MNIST数据集上的测试误差、参数量、内存占用和时间对比，验证了ODE-Net在资源效率上的优势。 |
| 表3 | LTC模型在多个时间序列数据集上的表现对比，显示其对比LSTM、CT-RNN等模型具有显著提升。 |
| 表4 | GRU与液态神经网络整体性能及显存用量对比，显存占用大幅度减少到原有5%左右。 |
| 表5 | 不同模型因子相关性矩阵，揭示了各模型学习到的因子存在差异，相关系数大约在0.69-0.82之间。 |
| 表6-10 | 2020-2024年分年度多头、多空组合收益、夏普比率、最大回撤等指标，体现了液态网络与GRU的可比表现和各自优势。 |
| 图1 | ResNet结构与ODE-Net连续模型的对比示意。 |
| 图2 | 伴随灵敏度方法反向传播原理图。 |
| 图4 | LTC神经元工作示意图，体现生物神经动态建模。 |
| 图8 | NCP模型噪声鲁棒性评估图，显示在自动驾驶任务中抗噪能力优于主流模型。 |
| 图11 | CFC闭式解与数值求解结果轨迹对比图，验证模型精度与效率。 |
| 图14 | CFC在自动驾驶视觉任务中的注意力热图，体现模型对关键车道线特征精准捕捉。 |
| 图15-24 | 各模型量化选股因子分档表现与RankIC表现图，直观展示模型有效性。 |

以上是本文重点图表的核心价值体现，助力读者理解技术细节和实证藏金。[page::2-3,5-6,7-10,11-14,15-20]

---

总结

本报告全方位介绍了神经常微分方程及液态神经网络在量化选股领域的理论基础、技术细节及实证结果，系统展示了其相较传统循环神经网络在模型效率、稳健性及策略表现上的优势。广发证券金工团队通过严谨的实验设计，证明了液态网络模型的广泛适用性和切实潜力，特别是NCP和CFC结构在资源受限情况下的卓越表现，为未来金融AI模型的发展提供了宝贵方向和借鉴。

---

以上内容均引自《广发金工：神经常微分方程与液态神经网络》完整报告原文 [page::0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]

报告