• 模型创新与理论保证 [page::3][page::4][page::12][page::15]：

- 提出首个将因子模型结构理论性地嵌入扩散生成模型的框架，即扩散因子模型。
- 利用资产收益的低维因子结构，通过时间变异正交投影分解得分函数，并设计结合编码器-解码器和残差连接的神经网络。
- 理论界定得分函数估计误差收敛率为 $\tilde{\mathcal{O}}(d^{5/2} n^{-\frac{2}{k+5}})$，主要依赖于因子维度 $k$，且对资产维度 $d$ 的依赖仅为多项式，缓解高维带来的“维度灾难” 。

• 扩散模型核心机制与得分分解 [page::6][page::9][page::10][page::11]：

- 扩散过程包含正向注入噪声与逆向生成流程，关键在于准确拟合未知得分函数——数据分布对数密度的梯度。
- 基于因子模型结构，将得分函数分解为“子空间得分”（针对因子空间，非线性）与“补偿得分”（线性，调节异质噪声协方差）。
- 该分解使得网络输入从高维降至因子维度，提升低样本环境中学习效率。
- 设计的网络结构体现估计函数表达形式，包含时间依赖的噪声校正矩阵以及低维映射。

• 统计学习与误差分析 [page::12][page::13][page::14][page::15]:

- 在因子分布满足二阶可微和次高斯尾部假设下，构建具备良好近似误差和估计误差界的神经网络家族。
- 近似误差依赖因子数$k$及平滑度，且近似网络规模随精度要求提升。
- 估计误差给出非渐近界，学习速率以因子维度为主要驱动，且多项式依赖资产维度$d$。
- 通过截断技术和覆盖数估计，证明了全局学习误差的高概率收敛性。

• 分布估计与潜在空间恢复 [page::16][page::17][page::18][page::19]:

- 拟合的扩散模型生成的数据分布在总变差距离意义上接近真实分布，误差界为 $\tilde{\mathcal{O}}(d^{5/4} n^{-\frac{1}{2(k+5)}})$。
- 利用生成样本的协方差矩阵，通过奇异值分解准确恢复潜在因子子空间，误差同样以因子维度为主导。
- 理论分析引入时变子空间及异质噪声处理的耦合技术，确保传播误差控制。

• 数值实验与实证分析 [page::20][page::21][page::22][page::23][page::24][page::25][page::26]:

- 合成数据下，资产数2048，因子数16, 展示扩散因子模型在小样本(少于资产维度)环境下超越经验PCA的潜在空间估计性能。
- 实证选用2001年至2024年美国股票数据，采用五年滚动窗口训练。
- 利用扩散生成数据估计均值和协方差，构建均值-方差最优投资组合，显著提升收益和夏普比率，较等权(EW)、市值加权(VW)、样本估计(Emp)、和收缩矩阵(Shr)方法表现优越。
- 对比三种使用扩散生成数据的组合策略（Diff+Emp、Diff+Shr、E-Diff），Diff+Emp获得最高投资回报及风险调整收益。
- 对股性因子抽取，扩散基因子相较传统Fama-French等因子模型，表现出更强系统性风险捕捉能力，改善了因子组合的夏普比率。

• 关键图示：

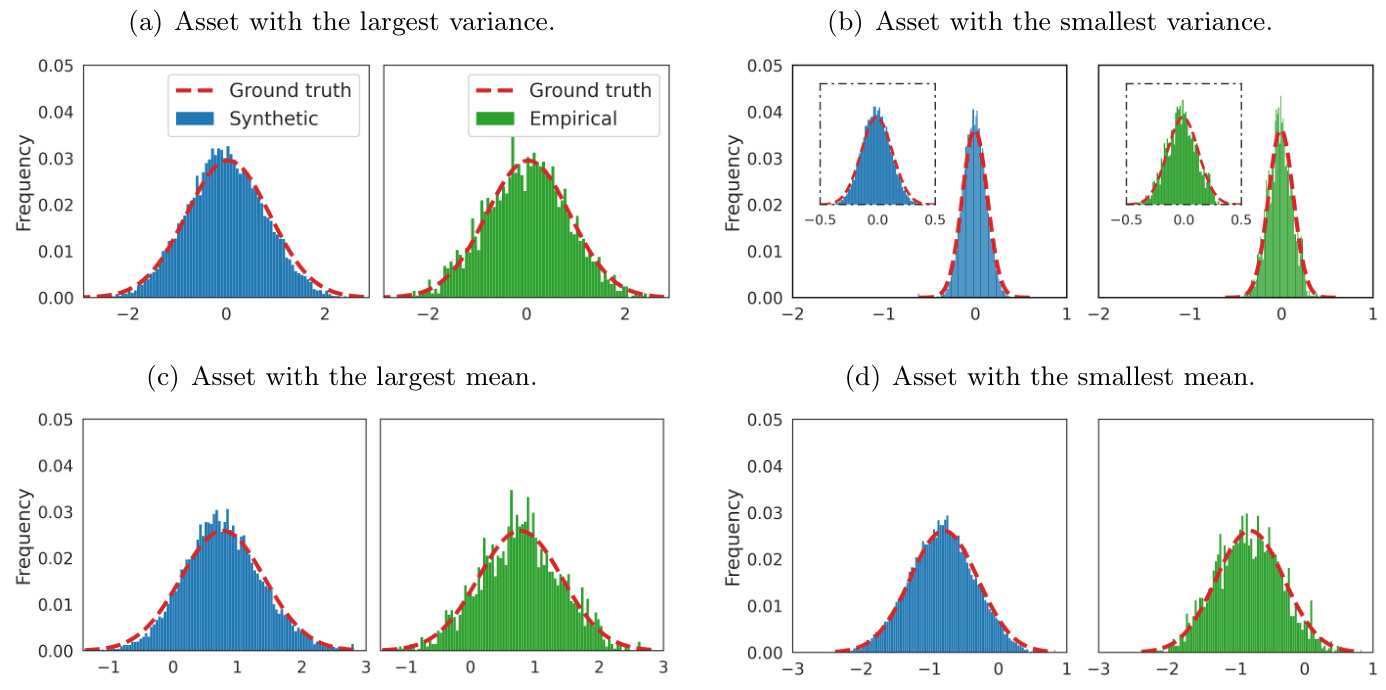
- 由扩散因子模型生成的单资产收益分布更平滑且更接近真实分布（图1）：


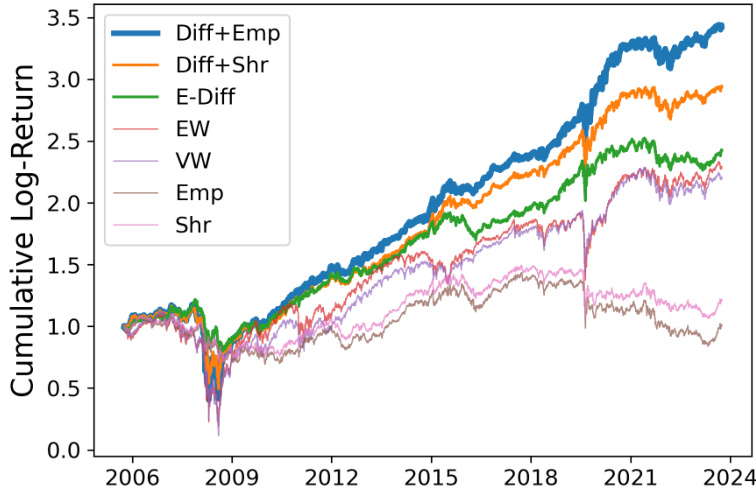
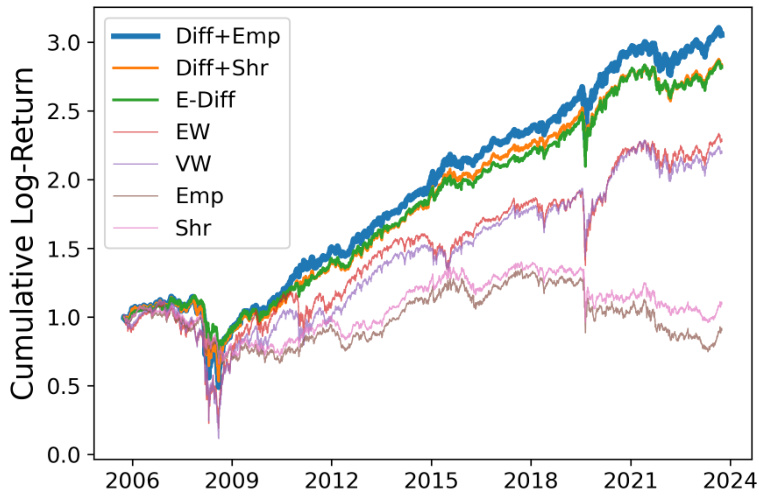
- 均值-方差组合表现（含交易成本）差异，Diff+Emp策略长期收益领先（图2）：


- 因子组合夏普比率显著提升，Diff+POET法性能优于经典因子模型（表3）。

专项分析报告 — 资深金融研究报告解析

报告名称

Diffusion Factor Models: Generating High-Dimensional Returns with Factor Structure
作者：Minshuo Chen, Renyuan Xu, Yumin Xu, Ruixun Zhang
发布时间：2025年4月10日
主题：金融高维资产收益的生成模型——融合因子模型与扩散模型的理论与实证研究

---

一、元数据与整体概览

本篇报告围绕设计与分析一种创新的高维资产收益生成模型——“扩散因子模型”（Diffusion Factor Model, DFM），旨在结合金融市场固有的因子结构与最新的生成扩散模型技术，用于风险管理与资产配置的场景仿真。作者团队由陈敏硕等四位学者组成，来自金融统计与机器学习交叉领域。本论文创新性地理论化地将经典的经济学因子模型（假设资产收益被少数潜在因子驱动）融合至生成扩散模型架构，解决了金融大规模资产（数千维）及样本容量有限时，传统生成模型“维度灾难”和数据稀缺问题。报告还提供了理论保证、数值仿真及现实股票市场的实证验证。

报告核心观点：

• 通过利用市场资产收益因子结构，扩散模型的Score函数可被分解成低维子空间及补充部分，减轻参数空间复杂度；

- 基于该结构设计神经网络架构，理论证明生成收益的统计误差主要受因子维度k控制，而非资产总数d；

• 数值实验和实证结果显示该方法在投资组合构建中的实际有效性，尤其在数据稀缺时更优于传统方法。

评级和目标价未涉及，报告为基础理论与应用研究性质，强调模型性能和金融经济意义。作者主旨在为高维金融数据生成带来新一代理论与实践工具。

---

二、章节逐段深度解读

2.1 引言（Sections 1 & 1.1）

关键论点

• 金融情景仿真是风险管理和投资组合优化的核心环节，特别是在样本有限与维度巨大时面临挑战。

- 传统方法无法满足现代市场快速复杂多变的需求，生成AI特别是扩散模型为金融数据仿真带来新机遇。

• 作者创新开发结合扩散模型和因子模型的“扩散因子模型”，统筹理论与实证，突破传统的非参数统计维度高依赖瓶颈。

理由与假设

• 金融资产收益存在低维“因子结构”——少数公共因子影响大量资产，赋予数据低维潜在流形性质。

- 扩散模型相比于GANs训练更稳定，基于随机微分方程的先进理论基础适合引入金融领域结构性假设。

• 随机过程理论赋予模型非渐近误差界保障，更适用于少量样本的金融时间序列。

---

2.2 “扩散因子模型”的模型假设与建构（Section 2）

关键论点

• 定义高维资产收益${\bf R} = \beta{\bf F} + \boldsymbol{\varepsilon}$，其中${\bf F}$为$k$维未知潜因子，$\beta$为因子载荷（$d\times k$矩阵），主题是训练扩散模型生成满足这一因子结构的高维数据。

- 扩散模型的核心为“score函数”$\nabla\log pt$的估计，属于随机微分方程（SDE）范围。

• 该模型利用了潜因子维度远小于资产维度这一事实，进行噪声归一化及子空间投影，提高训练样本效率。

理论推导

• 借助Ornstein-Uhlenbeck过程对资产收益注入正态噪声，设定与时长$t$相关的参数$(\alphat, ht)$刻画噪声收缩与注入量，方便相关SDE运动过程分析。

- 时间反转扩散过程理论使采样变为从标准高斯分布“反扩散”到目标数据分布，score函数估计是关键。

• 实际样本（$n$个）有限，采用“去噪得分匹配”训练模式，利用已知噪声性质解析score的隐式表达，解决不可计算问题。

---

3. Score 函数分解（Section 3）

关键论点

• 证明在因子模型结构下，扩散模型的score函数可被数学分解为“子空间分量”和“补充分量”，前者依赖于低维因子得分的得分函数，后者是与资产特有噪声相关的线性修正项。

- 这一分解基于对归一化和噪声协方差矩阵的运算，推导得到矩阵投影算子$\mathbf{T}t$与时间相关的噪声变化矩阵$\boldsymbol{\Lambda}t$。

• 该分解是模型设计的核心，指导神经网络架构设计，降低学习复杂度并针对结构设计跳接连接。

具体数据与假设

• 零假设：因子载荷矩阵$\beta$列正交，因子${\bf F}$服从密度$p{\rm fac}$且有二阶矩，残差向量$\boldsymbol{\varepsilon}$满足成分独立的高斯分布，带有非均匀方差。

- 利用高维资产收益的协方差拆分，定义正交射影算子和正交矩阵$\Gammat$辅助分解score函数。

• 换言之，score函数$\nabla \log pt({\bf r})$分解为：

$${\bf s}{\rm sub}({\bf z},t) = \mathbf{T}t \boldsymbol{\Lambda}t^{1/2} \beta \nabla \log pt^{\rm fac}(\cdot), \quad {\bf s}{\rm comp}({\bf r},t) = - \boldsymbol{\Lambda}t^{-1/2} (I - \mathbf{T}t) \boldsymbol{\Lambda}t^{-1/2} {\bf r}.$$

---

4. 神经网络架构设计与理论分析（Section 3.2 & 4）

设计思路

• 通过上述score函数的分解（子空间和补充两部分），设计编码器-解码器架构的神经网络，利用ReLU激活，含跳接连接，严格限制网络宽度、深度、权重范围等超参数空间，增强拟合和泛化能力。

- 子空间层面用较低维度的神经网络学习$\pmb{\xi}(\cdot)$函数，其输入经过了时间和噪声归一化处理；补充部分则为线性、可直接实现。

理论保证

• 定理1（网络逼近能力）说明该网络族在$L^2$范数意义下可以任意精度逼近目标score函数，误差上界与因子维度$k$相关，且不直接依赖资产维度$d$，网络规模随精度$\epsilon$的增加多项式增长。

- 定理2（估计误差与样本效率）给出基于$n$个样本估计score函数的非渐近估计误差界限，误差率主要由因子维度$k$控制，附带轻微的$d$次多项式因子，明显优于纯非参数依赖全维度的传统方法。

---

5. 分布估计及子空间恢复（Section 5）

该节贡献

• 基于估计的score函数，定义逆扩散过程生成的分布$\widehat{P}{t0}$，分析其与真实数据分布$P{\rm data}$的距离（总变差距离），以及能否准确恢复潜在因子子空间。

- 提出基于生成样本的协方差矩阵估计及奇异值分解(SVD)方案，以测量并恢复潜在因子空间，理论保证生成样本的协方差矩阵精度和主子空间误差均可控制。

关键结果（定理3）

• 总变差距离界为 $\tilde{O}\left( (1 + \sigma{\max}^k) d^{5/4} k^{\frac{k+10}{4}} n^{-\frac{1 - \delta(n)}{2(k+5)}} \log^{5/2} n \right)$ ，即生成数据分布与真实分布越逼近，误差随着样本数$n$以接近$1/(2(k+5))$的幂率衰减。

- 子空间估计误差包括奇异值和对应子空间的Frobenius范数误差与样本数$n$呈负幂关系，且依赖于因子辨识的特征值间隙和噪声峰值$\sigma{\max}$。

---

三、图表深度解读（重点图表）

表1（Section 6，Synthetic Data）

• 报告了“Diff Method”（基于扩散因子模型生成数据的PCA）与“Emp Method”（直接训练数据PCA）针对主因子特征值及主子空间的估计误差，随样本量变化。

- 观察：在样本量 $N \leq d=2048$ 时，Diff Method的误差明显低于Emp Method，优势在小样本规模更显著。

• 意义：芬方小数据环境下，扩散因子模型生成的数据更能提取潜因子结构，有效缓解样本稀缺问题。

图1（Section 6，Return Distribution）

• 选取最大/最小均值和方差的4只资产对比生成数据分布（蓝色）与真实数据（红色虚线），以及实际观测样本分布（绿色）。

- 结果显示生成的分布更加平滑，且更贴近真实分布，特别是在尾部和峰值形状上优于直接采样。

• 启示：扩散因子模型具备较强的金融资产分布生成能力，更好地捕获真实收益特征。

表2与图2（Section 7.1，Mean-Variance Optimal Portfolio）

• 表2衡量多种策略投资组合在含/不含交易成本下的表现，指标包括平均收益、波动率、夏普比率、确定等价收益率（CER）、最大回撤和换手率。

- “Diff+Emp”和“Diff+Shr”方法（利用生成数据改进均值协方差估计）均显著优于传统Empirical、Shrinkage及等权等基线，尤其夏普比率提升明显（约两倍于等权策略）。

• 累计收益图2进一步确认“Diff+Emp”组合表现稳健优越，呈现更高收益增长斜率。

- 说明：基于扩散因子模型生成的数据有效改善了协方差矩阵估计，带来资产配置实质提升。

表3与表4（Section 7.2，Factor Portfolio）

• 表3显示基于不同因子估计方法（PCA，POET，RPPCA）和“Diff+”对应生成数据版本的因子切线组合夏普比率比较。

- 结果突出：基于生成数据的因子组合夏普比率大幅优于传统FF模型和纯PCA类型方法，提升幅度3-5倍不等。

• 表4列出生成因子与FF传统因子的相关性，显示生成因子捕获了显著经济因素（市场风险、长期反转等），展现经济可解释性。

- 结论：扩散因子模型不仅提升因子估计质量，也使得投资组合更好捕捉系统风险因子。

---

四、估值分析

本报告没有具体涉及估值模型或价格预测，主要聚焦于生成资产收益分布和提取因子结构。不过，因子模型及协方差矩阵估计质量的提升典型地促进资产定价和投资组合优化，是估值环节的理论基础。理论保证和实证检验表明，DFM在生成资产回报时，也间接提高了基于这些生成数据的资产定价模型的效率和稳定性。

---

五、风险因素评估

报告对风险因素的识别主要围绕以下几点：

• 噪声异质性与建模复杂性：资产收益中的残差项具有非均匀方差，导致score函数分解及学习难度提升，需要引入时间变化正则和归一化处理。

- 小样本和高维维度：数据维度$d$巨大但样本量$n$有限，出现维度灾难风险。报告通过理论保证主控因子维度$k$缓解了这一风险。

• 模型误差累积：Score函数估计误差可能积累导致生成数据向真实分布偏离，报告提出早停时间$t0$平衡噪声注入和估计误差权衡风险。

- 子空间识别模糊：因子和载荷只可识别到线性变换，不确定性影响潜在因子解释，虽通过正交规范简化。

缓解策略主要通过理论设计、正则化、早停机制以及优化采样步骤实现。

---

六、批判性视角与细节解析

• 维数依赖和噪声假设：尽管算法主控因子维度，但仍对$d$存在轻微多项式依赖，此依赖来源于残差噪声覆盖整个$d$维空间。现实中噪声结构可能更复杂，影响泛化误差。

- 模型假设限制：残差被假设为独立高斯，高阶非线性因子或噪声结构不涵盖，目前模型对非高斯噪声适应能力尚未明确。

• 网络规模与实际部署：网络参数量巨大（近10亿级），在实际金融市场的低频数据下，训练成本和稳定性需关注，实操性待考。

- 潜在因子解的解释性：尽管因子相关性良好，但由于因子载荷的旋转性质，生成的潜因子可能难以直接经济解释。

• 早停时间选择：理论中早停时间$t0$调节误差平衡，实务中如何选择$t0$对生成效果影响极大，尚无完善自动化准则。

---

七、结论性综合

本报告提出了一种创新的融合金融因子模型结构与生成扩散模型的方法，系统构建了理论完善的模型框架及神经网络架构，并给出明确的非渐近误差界限，有效克服经典非参数方法在高维金融数据中因“维度诅咒”和“数据稀缺”带来的挑战。

理论分析显示，该方法在score函数估计和生成分布误差上的收敛速度主要依赖于潜因子维度$k$，而非资产维数$d$。该框架强调了score函数的分解策略，结合时间相关的投影和噪声归一化，由此设计出专门的编码解码网络结构。

数值模拟验证其在高维小数据设置下，能更准确恢复潜在因子子空间及生成资产收益分布。实证研究则证明基于该模型生成的数据在估计均值和协方差矩阵时显著提升，带来更优的均值-方差投资组合及因子投资组合，显著提升了夏普比率等关键经济指标。

总体来看，该报告开辟了金融高维资产生成建模的新方向，理论严密、模型创新、实证有力，是金融工程、量化投资及机器学习交叉领域的突破性贡献。

---

八、图表关键引用

• 表1、图1（第20-22页）: 小样本环境下，DFM生成数据优于经验PCA，子空间和顶特征值恢复误差显著降低。

- 表2、图2（第23-24页）: 利用DFM生成数据改进的投资组合策略在美国股市实证中表现出色，风险调整收益卓越。

• 表3、表4（第25-26页）: 基于DFM生成数据的因子估计显著提升因子切线组合夏普率，捕获经济重要因子。

- 图7.1、7.2清晰展示了DFM生成数据更合理的资产收益分布及经济意义。





---

九、专业术语简释

• 扩散模型（Diffusion Model）：一种基于随机微分方程的生成模型，依赖于数据分布的梯度（score函数），通过逆向扩散过程从噪声生成真实数据。

- Score函数：概率密度函数对数的梯度，核心目标是估计该函数以驱动逆向采样过程。

• 因子模型（Factor Model）：金融资产收益假定由少数公共因子线性组合及特有噪声两部分构成，$\mathbf{R}=\beta \mathbf{F} + \varepsilon$。

- 去噪得分匹配（Denoising Score Matching）：通过带噪声数据拟合score函数的技术，解决直接估计score困难的问题。

• 总变差距离（Total Variation Distance）：衡量两个概率分布差异的指标，越小代表生成分布越接近真实分布。

- 特征子空间恢复（Latent Subspace Recovery）：通过生成样本协方差矩阵的主特征分解，估计潜在因子空间，确保因子模型结构有效捕获。

• Davis-Kahan定理：用于线性代数中衡量特征空间变动与矩阵扰动之间的关系。

---

【本分析报告基于报告全文内容，引用及论据均以页码索引呈现，具体页码请参见原文】
（例如：[page::0], [page::3], [page::16], [page::24]）

报告