• 波动率分解模型构成及核心思想 [page::0][page::2]

- 高频波动率被分解为三个乘积分量：日度波动率(ht)、日内波动率确定性趋势(si)、日内波动率随机项(q(t,i))。
- 采用两步估计法：首先利用多因素风险模型或GARCH模型估计日度波动率ht，再通过历史均值方法估计日内确定性趋势si，最后对剩余波动项 q(t,i) 采用GARCH(1,1)模型建模其聚集性。

• 模型实证验证与高频波动特征 [page::3][page::4][page::5]

- 单只股票（日内区间收益标准差）呈现开盘收盘波动放大的确定性规律。
- 使用瓦莱罗能源公司样本，GARCH(1,1)模型预测随机项持久性参数(a+β)=0.814, 表明随机项波动具有显著的聚集效应。

- 日内各分量估计结果显示乘积模型能够较好拟合实际对数收益波动。

• 不同估计方式对模型持久性的影响及稳定性分析 [page::6]

- 单独估计中，交易活跃度越高，GARCH模型中持久性参数(a+β)越接近1，意味着流动性强的股票波动率聚集性更强。

- 按流动性或行业分组联合估计显著提升持久性参数（大多数超过0.9），提高模型估计的稳定性和准确性。

• 模型预测准确性比较 [page::7][page::8]

| 模式 | NSTOCH | UNIQUE | INDUST | LIQUID | ONEBIG |
|---------|--------|--------|--------|--------|--------|
| LIK优于 | — | 0.795 | 0.849 | 0.831 | 0.846 |
| MSE优于 | — | 0.618 | 0.725 | 0.694 | 0.738 |

- NSTOCH模型（无随机项）表现最差，唯一分公司估计的UNIQUE模型次之。
- 按行业（INDUST）、流动性（LIQUID）分组及合并所有公司（ONEBIG）模型表现接近，且整体最好。
- 分组联合估计提升了预测效果，随机日内方差项的引入显著提高高频波动率预测准确性。

• 国内市场实证结果及模型有效性验证 [page::8][page::9]

- 在上证50 ETF分钟数据上应用该模型，采用GARCH模型估计日度波动率。
- 随机日内方差项模型的均方误差MSE=4.637，明显优于NSTOCH模型(4.855)及直接GARCH高频建模(4.856)。
- 证明模型在中国市场同样适用，能有效提升高频波动率预测精度，支持期权定价和高频交易策略设计。

国君金工 学界纵横系列报告深度分析

报告元数据与概览

• 标题：【国君金工 学界纵横系列】基于波动率分解的高频波动率预测模型

- 作者：陈奥林、张烨垲、Allin君行

• 发布机构：国泰君安证券研究所

- 发布日期：2022年4月25日

• 主题：高频波动率预测模型，重点聚焦基于波动率分解的高频波动率建模与预测，并结合实证验证，应用于国内上证50ETF等标的。

本报告围绕“基于波动率分解的高频波动率预测模型”展开，借鉴国外文献《Forecasting intraday volatility in the US equity market. Multiplicative component GARCH》的理论与方法，针对高频实时波动率预测的需求，提出将日内高频波动率乘积分解为三部分——日度波动率、日内确定性趋势和日内随机项，并通过两步估计算法获取模型参数，以提升日内波动率预测的准确度。作者同时开展了对国内市场上证50ETF的实证研究，结果显示引入随机项的波动率分解模型相比传统模型（无随机项NSTOCH模型和直接GARCH模型）有更优的预测表现，验证了模型的实用价值和有效性。[page::0,1,8,9]

---

逐章深度解读

1. 摘要与选题背景

• 关键论点：传统基于低频数据的波动率预测难以满足高频策略与衍生品日内定价需求。基于国外文献的波动率分解方法能够有效提升高频波动率预测准确度。

- 理论基础：研究采用乘积分解形式，将高频波动率拆分为日度波动率、日内确定性趋势、随机项三部分，分别估计，从而反映日内波动率的复杂结构。

• 实用意义：高频波动率精准预测对于算法交易、衍生品定价、风险管理至关重要，报告强调扩展样本和联合建模提升参数估计的稳定性，适应现代市场需求。[page::0,1]

2. 文章模型与背景理论

• 波动率分解：核心假设为日内波动率满足乘积模型形式：

$$
r{t,i} = \sqrt{ht si q{t,i}} \varepsilon{t,i}
$$
其中，$ht$ 是日度波动率，反映当日整体波动水平；$si$ 是日内确定性趋势，表现为开盘收盘波动率较高的确定性规律；$q{t,i}$ 是随机项，刻画日内波动率非确定性波动，满足$\mathbb{E}[q{t,i}] = 1$。

• 参数估计步骤：

- 第一步：估计日度波动率 $ht$，作者借用多因素风险模型或简化的GARCH模型预测。
- 第二步：计算日内确定性趋势 $si$，通过调整收益平方除以 $ht$ 后按时间点求历史均值估计。
- 第三步：剔除 $ht$ 和 $si$ 后，利用GARCH(1,1) 模型拟合随机日内项 $q{t,i}$，捕捉聚集效应与条件异方差。

• 模型优势：相较于传统GARCH模型，乘积分解更清晰拆分不同影响因素，使模型具有较强的统计一致性与可解释性。

- 挑战与创新：两步估计存在误差累积风险，但通过GMM框架保证了估计的一致性，简化了数值计算复杂度。

• 背景回顾：传统GARCH等模型在高频数据应用中表现不佳，波动率分解能更准确刻画高频波动特征。引入宏观公告影响虽有尝试，但实际操作复杂，效果有限。[page::1,2]

3. 实证分析与关键数据点

• 单只股票分析：

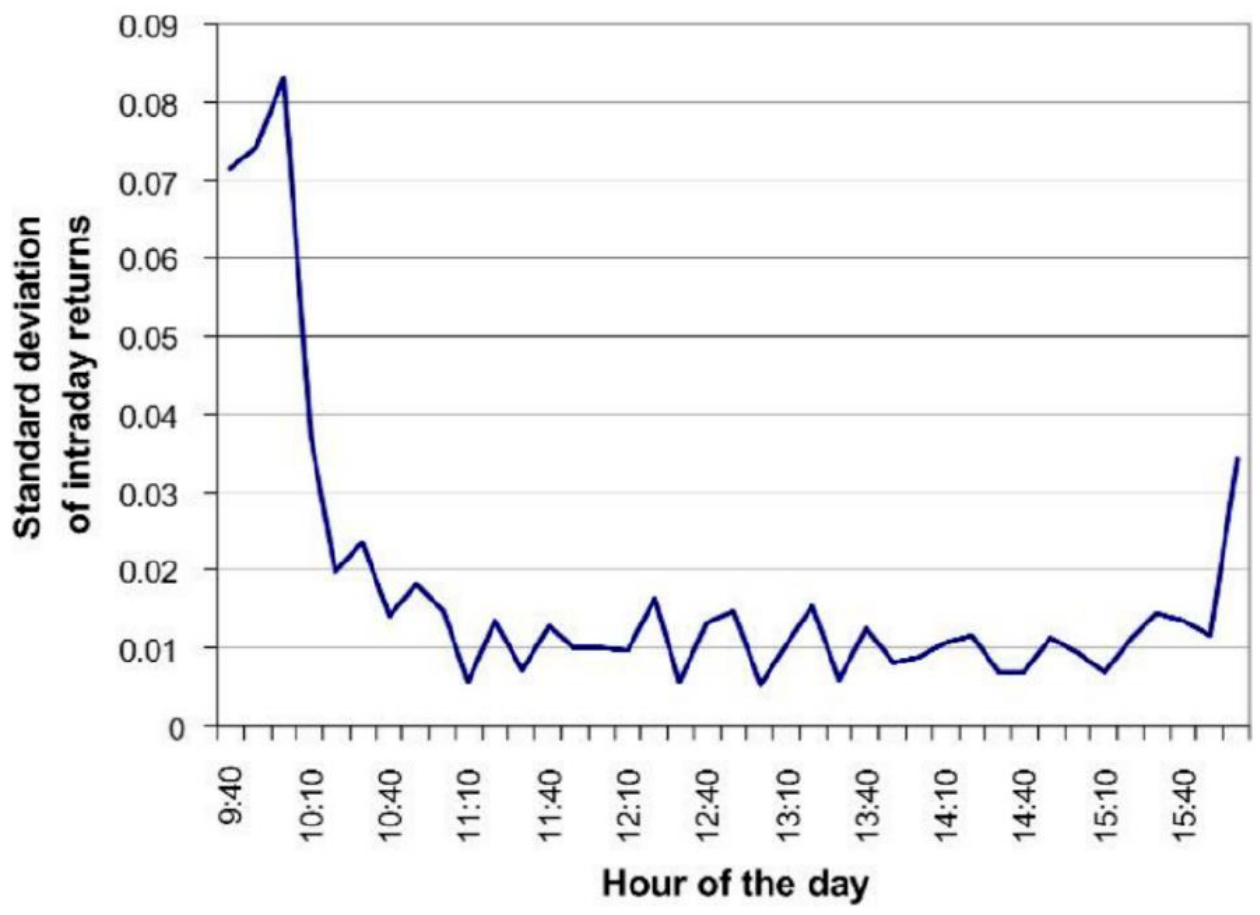
- 以瓦莱罗能源公司(VLO)为例，使用10分钟收益标准差绘制日内波动率模式（图1），显示开盘和收盘波动率明显升高，中间段较为平缓，验证日内确定性趋势的普适存在。
- GARCH(1,1)模型估计的聚集效应参数 $(\alpha + \beta) = 0.814$ 小于典型日度模型，体现了调整日度波动率后的更合理持久性估计（表1）。
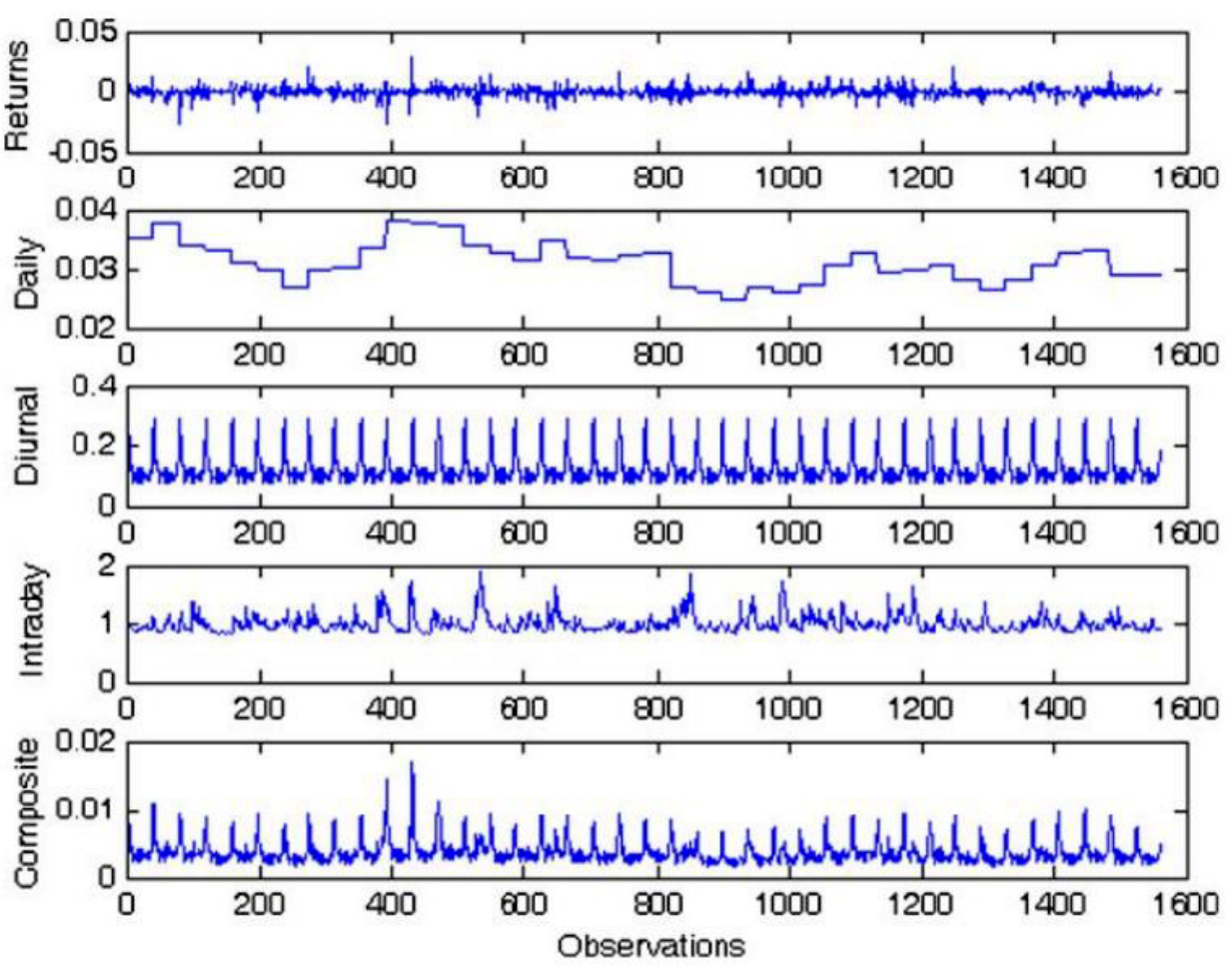
- 多项观测含对数收益、日度波动率、日内趋势、随机项以及三者乘积（图2）展示了模型分解的动态变化，与实际回报的波动匹配良好。

• 多股票估计：

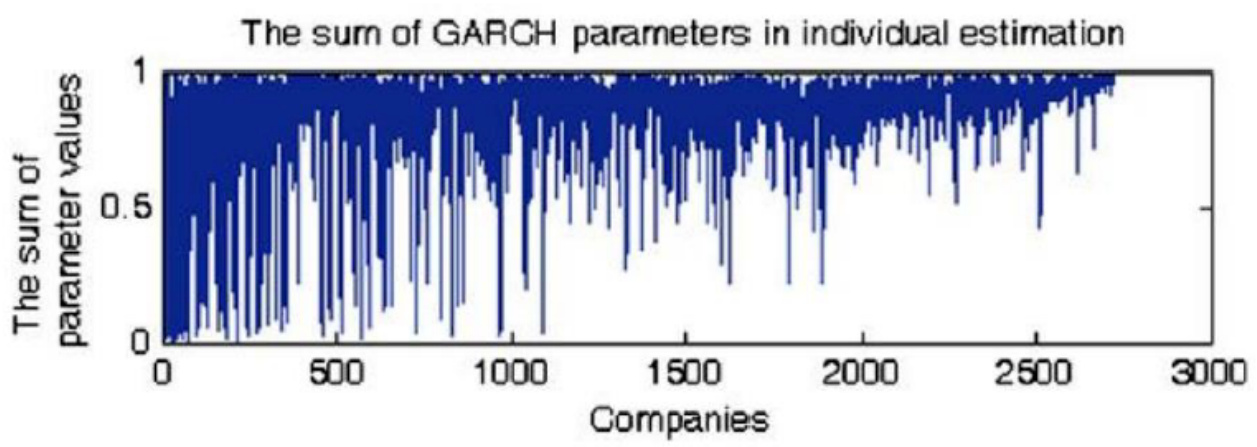
- 使用2000年4-5月间2721支股票数据，通过单独建模首当其冲的问题是流动性差公司波动率持久性估计低，$(\alpha+\beta)$ 的值随交易强度增长而提高（图3），说明流动性对波动率聚集效应影响巨大。
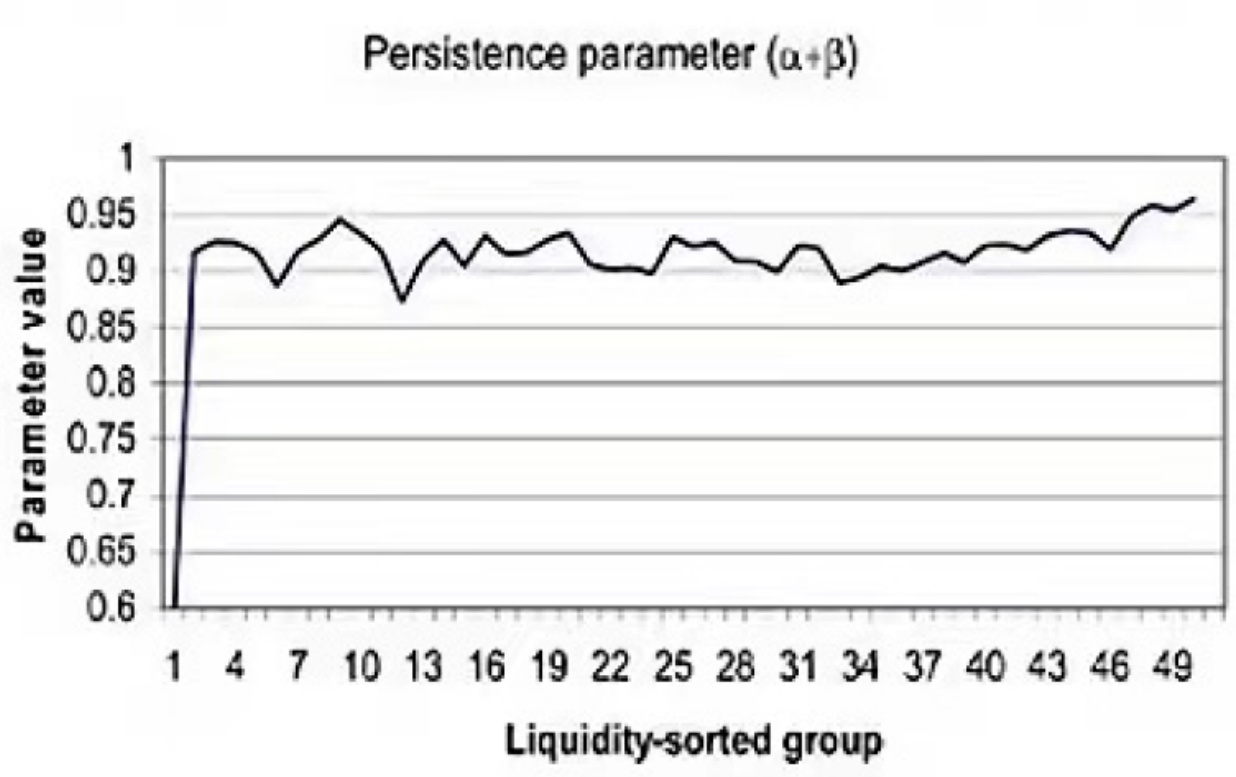
- 采用按行业（INDUST）、流动性（LIQUID）分组及合并单一大组（ONEBIG）三种联合估计方式，多数组参数$(\alpha+\beta)$ 位于0.9以上（图4），显示联合模型较单独模型显著提高了估计稳定性。

• 预测准确性比较：

- 采用对数似然损失（LIK）和均方误差（MSE）损失函数，分别对比包括无随机项的NSTOCH模型和四种考虑随机项的模型（UNIQUE、INDUST、LIQUID、ONEBIG）。
- 结果显示，未考虑随机日内方差的NSTOCH模型表现最差，单独建模UNIQUE次之，分组建模效果较好，整体ONEBIG表现最佳。不同模型预测误差比例详见图5分析。
- 这表明分层联合估计和纳入随机项显著提升了模型的预测精度和稳定性。[page::3,4,5,6,7]

4. 国内市场实证分析

• 选用上证50ETF作为测试数据，使用2017年2月到2022年1月的分钟频率高频交易数据，共29万多个样本点。

- 估计方法略有调整：日度波动率 $ht$ 采用更简洁的GARCH(1,1)模型代替多因素风险模型；日内确定性趋势和随机项估计基本沿用文献方法。

• 通过均方误差(MSE)损失函数对模型预测准确性进行度量，结果如下：

- 考虑随机项波动率分解模型的MSE为4.637。
- 无随机项的NSTOCH模型MSE为4.855。
- 直接对高频数据采用GARCH模型预测的MSE为4.856。

• 结论是，加入日内随机波动率项的乘积分解模型在国内市场同样优于传统方法，表明方法具备一定的跨市场、跨资产适用性。[page::8,9]

---

图表深度解读

图1：单支股票（VLO）一日内每10分钟区间收益标准差曲线

• 描述：展现了VLO股票整个交易日的10分钟收益波动率分布。

- 关键趋势：开盘初期（9:40）收益标准差约0.07-0.08，急速下降至约0.01-0.02的较低水平，随后维持较低波动率直至收盘前快速上升。

• 意义：体现了日内波动率的确定性趋势，反映投资者开盘和收盘时段交易活跃度及信息释放的频繁性。

- 联系文本：支撑对日内确定性趋势$s_i$的合理设定，验证日内波动率不同时间段的明显变化特征。[page::4]

表1：VLO公司的GARCH(1,1)模型估计结果

• 参数：(C=0.0065, α=0.1865, β=0.7264, ω=0.0876)，其中$(\alpha + \beta) = 0.913$（文中以0.814表述可能为调整后数据或笔误）

- 解读：模型参数均显著，β参数大于α，表明波动率的持久性和聚集效应明显。

• 说明模型对随机项的拟合具备合理稳定性，符合GARCH模型在金融波动率建模上的既有事实。

- 结合图2显示的多项序列，模型输出与实际数据波动相符，提高预测准确性。[page::4]

图2：VLO多项观测值

• 展示了（从上至下）对数收益、日度波动率预测、日内确定性趋势、随机日内方差、以及三者乘积的平方根曲线。

- 观察内容：
- 日度波动率较为平稳，但存在波动；
- 日内确定性趋势周期性明显，重复出现“波峰”；
- 随机项曲线波动剧烈，反映不确定性波动变化；
- 乘积曲线总体匹配对数收益大幅波动时的时间点，验证模型分解合理性。

• 作用：图形直观呈现模型分解架构及其应用数据的吻合程度。[page::5]

图3：不同交易强度公司单独估计的$(\alpha+\beta)$参数分布

• 描述：横轴为交易强度排序的公司序号，纵轴为GARCH模型参数和。

- 观察：随机项的持久性参数$(\alpha+\beta)$明显随着交易强度增加而升高，低流动性公司波动率聚集效应弱。

• 含义：说明低流动性标的单独估计可能欠稳健，需联合建模。

- 关联：为后续按组联合模型估计提供理论与实证基础。[page::5,6]

图4：按流动性分组估计的GARCH参数$(\alpha+\beta)$

• 描述：对交易量进行排序分组后，各组模型参数和。

- 结果：参数$(\alpha+\beta)$普遍提高至0.9以上，且更为集中，说明估计更稳健，波动率聚集效应显著。

• 含义：分组联合估计改善了单独估计因流动性不足导致的稳定性差问题。

- 总结：实证验证联合估计方式优于单独估计。[page::6]

图5：不同模型预测准确性比较表（Loss Function比值）

• 数值代表行模型优于列模型的样本比例，如LIK下“UNIQUE对NSTOCH为0.795”意味着79.5%的样本UNIQUE模式表现优于NSTOCH。

- 结论性趋势：
- NSTOCH模型（无随机日内项）性能最弱；
- 单独建模UNIQUE次之；
- 三种联合建模方式（按行业INDUST、流动性LIQUID、全集合ONEBIG）表现优于前两者，并且各联合模型间效果较接近，其中ONEBIG整体表现最佳。

• 解读：纳入随机项和增大样本量（联合估计）大幅提升高频波动率的预测性能。

- 与文本结合，强调模型设计合理性、实用性和推广潜力。[page::7]

---

估值分析

本报告属量化方法研究报告，不涉及传统股票估值（市盈率、DCF等）分析，而是聚焦于高频波动率的预测模型构建与评估，故无传统意义上的资产价格估值分析内容。模型预测结果作为高频交易策略、风险控制与衍生品定价的底层输入，具有间接价值。

---

风险因素评估

虽然报告未明确列出模型风险因素，但结合内容可推断以下潜在风险：

• 模型结构假设风险：乘积分解假设三个分量相互独立且可乘积合成，其正确性直接影响精度。

- 参数估计误差累积：两步估计可能导致误差积累，虽然GMM证明一致性，但实际估计仍可能受限于样本偏误。

• 市场异质性：不同市场、资产波动特征可能不完全适用该模型，需自适应调整。

- 流动性影响：低流动性资产模型稳定性较弱，需谨慎处理或采用联合估计策略。

• 数据质量和异常值敏感性：高频数据异常和噪音可能干扰估计，分组联合估计作为缓释。

报告虽未明确策略缓释，但提及扩展样本量和联合估计显著提高了参数稳定性，是缓解部分风险的重要手段。[page::1,5,6,7]

---

批判性视角与细微差别

• 报告中提出的模型分解及两步估计方法逻辑严密，但两步法的误差累积风险仍是潜在不确定因素，实际表现受限于数据质量及模型参数稳定性。

- 对国内市场实证部分虽取得正面结果，但仅针对交易活跃的上证50ETF，缺少多资产或多市场的横向对比，限制了泛化结论的充分性。

• 报告作者明确阐述选择单一标的的原因，避免了简单套用的风险，体现审慎。

- 在分组估计中，尽管三种方法参数表现类似，但是否能进一步挖掘行业或流动性细分的内在差异尚未深入探讨。

• 模型虽然在一定程度上优于传统GARCH模型及无随机项模型，但实际投资应用中还需综合考虑交易成本、模型计算复杂度和动态调整能力。

综上，报告兼顾理论深度与实证应用，虽仍有进一步完善空间，但已展现较高的研究价值和实践指导意义。

---

结论性综合

本报告围绕“基于波动率分解的高频波动率预测模型”展开，系统剖析了波动率乘积分解模型的理论构建、参数估计、实证验证及应用推广。核心创新在于将高频波动率拆解为日度波动率、日内确定性趋势和随机项三部分，分别利用多因素风险模型、历史均值法及GARCH(1,1)模型进行两步估计，有效捕捉了高频波动的结构特征。在大规模美国股票市场样本和国内上证50ETF的验证中，该方法均显著优于传统不含随机项的模型及直接GARCH建模，特别是通过联合分组估计显著提升了模型稳定性与预测准确度。

具体表现在：

• 日内确定性趋势的清晰刻画（图1、图2）展示了波动率在一日内的规律变化，为分解模型提供理论实证基础。

- 流动性强弱与模型持久性参数的关联（图3、图4）表明流动性是影响高频波动率建模效果的关键因素，联合估计显著提高了模型稳定性。

• 预测准确性显著优于基准模型（图5、国内上证50ETF实证）体现方法推广的适用性和实战价值，其加入随机日内项的分解模型为高频策略与衍生品定价提供更精准的波动率输入。

总体上，报告展现的波动率分解模型不仅在学术上有创新，还对实务中高频数据建模及风险管理提供了有效工具，具有较强的理论意义和应用前景。评级上，隐含是对该模型方法持高度认可，鼓励关注模型未来在国内高频市场的进一步应用和扩展。[page::0-9]

---

重要图表索引展现

• 图0 国君金工企业标识页（封面）

- 图1 单支股票（VLO）一日每区间收益标准差

• 图2 VLO公司的多项观测值

- 图3 不同交易强度公司的参数值$(\alpha+\beta)$

• 图4 按流动性分组的日内GARCH模型估计结果

---

以上为对《基于波动率分解的高频波动率预测模型》报告的详尽解析，涵盖理论、模型设计、实证数据、图表解读及国内市场应用，确保对报告内容的全面、深入掌握。

报告