• 基于扩散模型的金融时间序列去噪方法概述 [page::0][page::2]

- 利用条件扩散模型的前向加噪和反向去噪过程，逐步去除股价时间序列中的噪声。
- 采用Transformer结构作为score网络，训练时引入了无条件引导与条件引导的融合策略（classifier-free guidance）。
- 推理阶段结合总变差（TV）损失与傅里叶域损失作为辅助指导以提升平滑性与频域特征保持。

• 数据集与实验设置 [page::4]

- 使用三个不同频率的美股S&P500股票数据（日频、小时频、5分钟频），采用滑动窗口构建长度为60的时间序列样本，训练与测试集比例为4:1。
- 比较基准包括原始序列（Ori）、指数移动平均（EMA）、去噪自编码器（DAE）与基于扩散模型的去噪序列（VE-SDE和VP-SDE）。

• 去噪时间序列特性与指标表现 [page::5]

| 方法 | 1day DC@0.01 | 1hour DC@0.01 | 5min DC@0.001 |
|-------|-------------|--------------|--------------|
| Ori | 18.15 | 6.16 | 13.45 |
| EMA | 8.96 | 3.76 | 6.63 |
| DAE | 5.72 | 2.52 | 7.24 |
| VE-SDE| 5.98 | 4.04 | 4.46 |
| VP-SDE| 6.50 | 3.81 | 5.00 |

- 扩散模型去噪后数据的趋势变化事件（Directional Change）数量介于EMA和DAE之间，反映出对市场趋势的较好保持能力。
- VE-SDE与VP-SDE在小时频数据中趋势变化事件保留更多，表明保留了一定的市场波动细节。

• 下游收益率分类预测任务表现 [page::5]

| 数据集 | 方法 | F1-Score (1 step) | MCC (1 step) |
|--------|--------|------------------|--------------|
| 1day | Ori | 0.604 | 0.014 |
| | EMA | 0.656 | 0.120 |
| | DAE | 0.676 | 0.183 |
| | VE-SDE | 0.720 | 0.332 |
| | VP-SDE | 0.719 | 0.323 |

- 扩散模型去噪序列显著提升了未来收益率的分类性能，F1分数和MCC均显著优于其他方法。

- 去噪后的收益率分布更平滑，标签分布更分散，反映出“内在平滑”与“外部锐化”的双重效应，利于提升分类器性能。

• 基于去噪序列的交易信号生成表现 [page::6]

- 使用MACD和Bollinger指标，扩散模型去噪序列生成的交易信号在日频和小时频数据上表现最佳，交易次数较少以降低成本，交易收益更高。
- DAE方法因过度平滑，在高频数据中交易信号失效，无法触发交易。

• 利用分类器预测结果判定市场噪声实现动态交易策略 [page::6][page::7]

- 将分类器预测的市场趋势与实际市场趋势对比以判断噪声状态，噪声大时采用逆势策略，噪声小时采用顺势策略。
- 扩散模型去噪序列在1日和5分钟频数据上逆势交易表现优异，在1小时频数据上顺势交易效果更好。
- 该动态策略利用噪声水平信息，实现了更加精细的交易决策，提升了综合交易绩效。

• 量化因子与策略总结 [page::2][page::3][page::5][page::6]

- 因子构建：基于条件扩散模型对不同噪声水平的时间序列进行建模，融合条件引导（classifier-free guidance）策略和辅助损失（TV及傅里叶损失）提升去噪性能。
- 策略应用：将去噪序列应用于技术指标（MACD、Bollinger）交易信号产生，结合机器学习分类器输出的去噪市场趋势动态调整交易方向（顺势/逆势）。
- 回测结果显示，融合扩散模型去噪的策略在各数据频率均取得了更高收益和更低交易次数，夏普率和胜率提升明显。

金融时间序列去噪器基于扩散模型的详尽分析报告

---

1. 元数据与报告概览

报告标题：A Financial Time Series Denoiser Based on Diffusion Models
作者：Zhuohan Wang、Carmine Ventre
所属机构：英国伦敦国王学院 (King’s College London)
发布时间：2024年，发表于第5届ACM国际金融人工智能会议（ICAIF 2024）
主题：本报告聚焦于金融时间序列的数据去噪问题，探讨了扩散模型如何作为一种先进生成模型框架，提升金融时间序列的信噪比，从而增强数据预测能力与交易表现。

核心论点：
传统金融时间序列面临低信噪比问题，噪音扰乱数据解读和预测。基于生成式模型中扩散模型的最新进展，报告提出了一种条件扩散模型去噪方法，通过逐步加噪及去噪的正逆过程恢复金融信号。实验显示，扩散模型去噪后的时间序列在未来回报分类及交易策略中表现优异，实现更高收益、低交易频次，从而提高交易效率。此外，训练在去噪序列上的分类器可判定市场噪声水平，并以此设计新型交易策略获得超额收益。

该报告核心信息为：

• 通过条件扩散模型有效去噪金融时间序列，解决低信噪比问题；

- 去噪后数据提升未来回报预测准确率；

• 生成基于去噪时间序列的交易信号，提高收益并减少交易频次；

- 可判别市场噪声状态，指导差异化的交易策略。

---

2. 逐节深度解读

2.1 引言 (第0页)

• 关键论点：金融时间序列固有的低信噪比导致预测困难，传统模型受噪声影响性能下降。扩散模型作为新兴生成模型，具备通过正向（加噪）与逆向（去噪）过程逐步恢复原始数据的能力，表现优于传统方法。受到其在计算机视觉中的成功启发，尝试将该模型用于金融时间序列的去噪并验证交易应用效果。
• 推理依据：扩散模型包含正向噪声逐步施加和逆向去噪的Markov过程，能够学习数据分布的score函数（概率密度梯度），理论上保证得到高质量样本。前人工作显示，扩散模型在图像生成与对抗攻击防御方面成效显著，具备实际应用潜力。
• 总结贡献：文中明确提到三点贡献：(1) 利用条件扩散模型有效去噪，提升时间序列在收益预测任务中的表现；(2) 去噪数据驱动的技术指标信号生成更优交易表现并降低交易次数；(3) 利用去噪序列训练的分类器辅助判别市场噪声，进而设计更优交易策略。

---

2.2 相关工作 (第0-1页)

• 关键论点：介绍了扩散模型理论发展脉络及其在时间序列领域的应用，以及金融时间序列去噪传统方法。
• 扩散模型理论：

- 两大主流思路：一是DDPM（Denoising Diffusion Probabilistic Model）方法，基于Markov链的正/逆过程及变分推断框架；二是Score-based Generative Models (SGM)，通过学习数据分布的梯度函数(score)，用Langevin动力学迭代采样。两者可由随机微分方程(SDE)统一理论描述。

• 扩散模型在时间序列上的应用：主要分为预测、插补、生成三个方面，分别对应Auto-regressive模型TimeGrad、SDE框架下的ScoreGrad，以及多种生成模型。相关工作包括使用transformer架构进行条件扩散建模。
• 金融时间序列去噪：现行方法多依赖Fourier变换、Wavelet变换以及Denoising Autoencoder（DAE）等传统深度学习架构。DAE已被证明可提升下游任务表现。

---

2.3 Score Based Generative Model基础 (第1-2页)

• 关键论点：本节系统梳理了SGM的数学基础及其与DDPM的统一视角，重点解释了score函数的定义、训练目标及采样原理。
• 推理及重要概念：

- Score定义为数据概率密度对输入的梯度。通过训练神经网络$s\theta$拟合该梯度，利用噪声扰动数据实现去噪score匹配，避免直接计算高成本的Hessian矩阵迹。
- Langevin 动力学作为采样算法，通过梯度上升调整噪声样本，使其逐步趋向真实数据分布，实现数据生成。
- DDPM可视为层级隐变量模型，正向过程加噪符合预设的beta调度，逆向过程通过估计score函数逐步去噪。
- 随机微分方程(SDE)框架提供了上述方法的更为优雅且统一的连续时域表达，区分出Variance Exploding (VE)和Variance Preserving (VP)两种转移过程。

• 数学表达清晰简明，训练目标与采样步骤详实呈现，奠定了本文后续方法的理论基础。

---

2.4 方法论 (第2-3页)

• 2.4.1 问题表述：

输入时间序列$\mathbf{x} \in \mathbb{R}^L$，条件序列$\mathbf{c} \in \mathbb{R}^L$，输出去噪序列$\hat{\mathbf{x}}$。模型采用条件扩散score网络$s\theta(\mathbf{x}, t, \mathbf{c})$，利用transformer架构（借鉴CSDI）完成训练。参数细节公开，如3层MLP做条件嵌入，卷积层输出通道数64，8头注意力机制。

• 2.4.2 训练与推断：

- 训练：在最大噪声等级T=1内均匀采样噪声时刻$t$，对原序列$x0$施加前向扩散，加噪数据$xt$用于训练。
- 推断：采用noising-denoising流程，定义一个较小的噪声等级$T' < T$，使数据被适度扰动；同时输入条件$c = x0$保证去噪保持原始趋势，解决$T'$难以理论确定的问题。
- 引入Classifier-Free Guidance策略结合条件与无条件扩散模型提高采样质量，调节指导权重$\omega$，即为采样方向权衡。
- 推断中用到两类辅助loss：Total Variation (TV) Loss平滑增强时序趋势，Fourier Loss基于频域滤波保持有效频段，抑制噪声频段。
- Predictor-Corrector采样器结合随机微分方程和蒙特卡洛采样，提升去噪过程效果，且通过多随机种子平均降低采样随机性，保证去噪稳定性。

• 算法1与算法2完整呈现训练与推断流程，技术实现清晰。

---

2.5 实验设计及结果分析 (第4-7页)

2.5.1 数据集 (第4页)

• 采用三组频率不同的时间序列数据：1日频(2014-2023)、1小时频(2023-2024)、5分钟频(2024-2024)，均选美股标普500成分股，采用滑动窗口60步长、步幅20生成样本。训练与测试比例4:1，样本量分别为：47,807时序（1天）、25,985（1小时）、51,794（5分钟）。

2.5.2 去噪时间序列的基本特性 (第4-5页)

• 使用原始价格序列（Ori）、指数移动均线（EMA）、DAE及本文所提VE-SDE和VP-SDE方法去噪后序列，观察样本。

- 通过“方向性变化事件数（Directional Change, DC）”衡量市场趋势跳变，间接反映信噪比。表1数据显示:
- DAE在多数阈值下表现为DC最少，趋势较平滑但可能过度平滑；
- VE/VP-SDE方法在1小时数据集保持更多DC事件，保留更多真实变动；
- 5分钟数据中，VE/VP-SDE DC事件数略低于Ori，但仍较DAE更活跃。

2.5.3 下游分类任务 (第4-5页)

• 设计二分类任务预测未来对数收益的正负，使用基于集成树的分类模型训练及测试，评估数个预测长度（1、5、10步）。

- 指标采用F1分数和马修斯相关系数(MCC)，噪声步骤$T'$变化对性能无明显影响，显示模型稳定性。

• 表2展示扩散模型（VE-SDE、VP-SDE）方法在三个数据频率下大部分配置优于传统DAE和EMA，尤其MCC表现提升明显，反映对不平衡类别的判别能力增强。

- 通过图3的回报分布对比，作者提出“内部平滑”（去除数据细节噪音使数据更平滑）与“外部锐化”（标签分布更宽，增强预测空间区分度）的双重效果，说明扩散去噪方法提升了数据的可预测性。

2.5.4 去噪时间序列用于交易 (第5-6页)

• 选用4只标普500权重股(GOOG,AAPL,MSFT,AMZN)，基于去噪序列生成技术指标信号并在原始价格上回测。

- 采用MACD指标和Bollinger策略，分别记录多头收益(LOR)、多空收益(LSR)及交易次数(NoT)。

• 结果见图4，

- MACD策略下，扩散模型去噪时序在日频、时频表现最佳，短频率分辨率DAE稍优；
- Bollinger策略中，扩散模型去噪方法几乎全胜其他模型，DAE因平滑过度减少了交易信号，导致交易次数及交易激活明显不足，验证了表1中DC事件少的现象分析。

2.5.5 利用分类器预测辅助交易 (第6-7页)

• 在前述分类任务训练的模型基础上，分析在预测阶段对市场趋势噪声的识别能力，并设计跟随趋势与逆势反向策略。

- 通过比较预测阶段的市场趋势与真实趋势，判断市场是否处于“噪声”状态。噪声市场应采用反向策略，无噪声市场采用跟随策略。

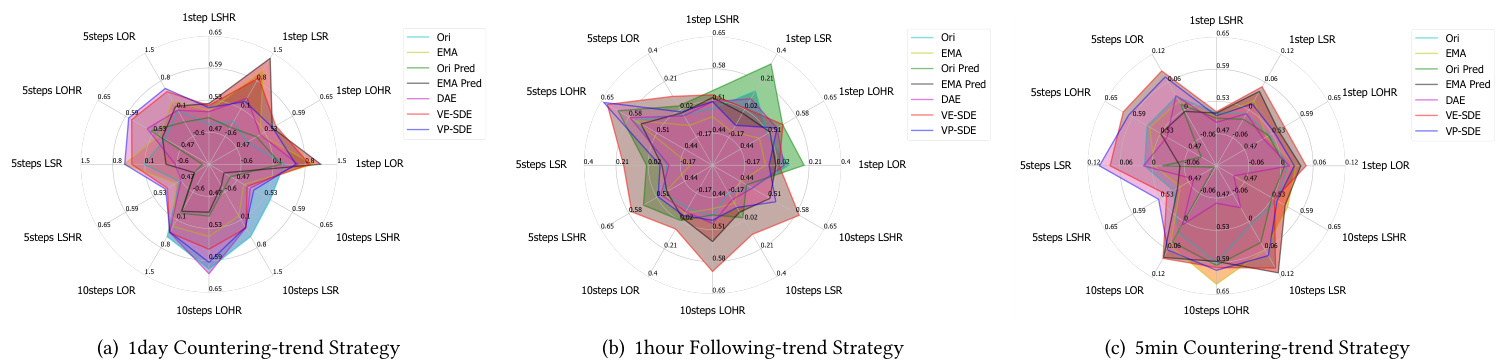
• 图5雷达图结果显示，扩散模型去噪序列训练的分类器在不同频率和预测时长下表现优异，尤其在1日和5分钟尺度上逆势策略效果更好，1小时尺度跟随策略更有利，合逻辑地反映了噪声与趋势稳定性不同场景下的差异。

- 结合5.3中DC事件的统计，进一步佐证1小时尺度市场噪声较少，保持趋势延续；1日与5分存在更多噪声，需逆势操作。

---

3. 图表深度解读

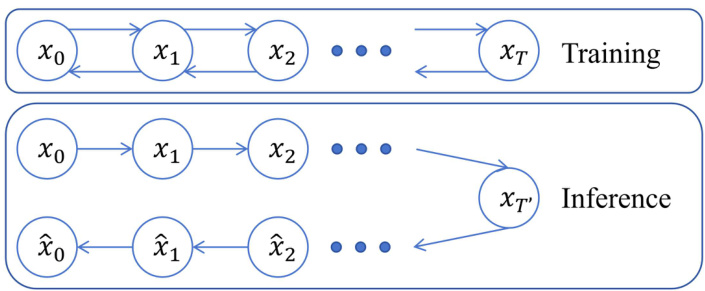
3.1 图1：训练与推断流程示意图 (第2页)

• 图示简明展现扩散模型的训练阶段（正向加噪）及推断阶段（逆向去噪）过程，从$x0$到$xT$的正向链路，加噪至最大噪声，反向链路逐步去噪达到$\hat{x}0$。辅以条件引导，保证推断时重建趋势保持稳定。

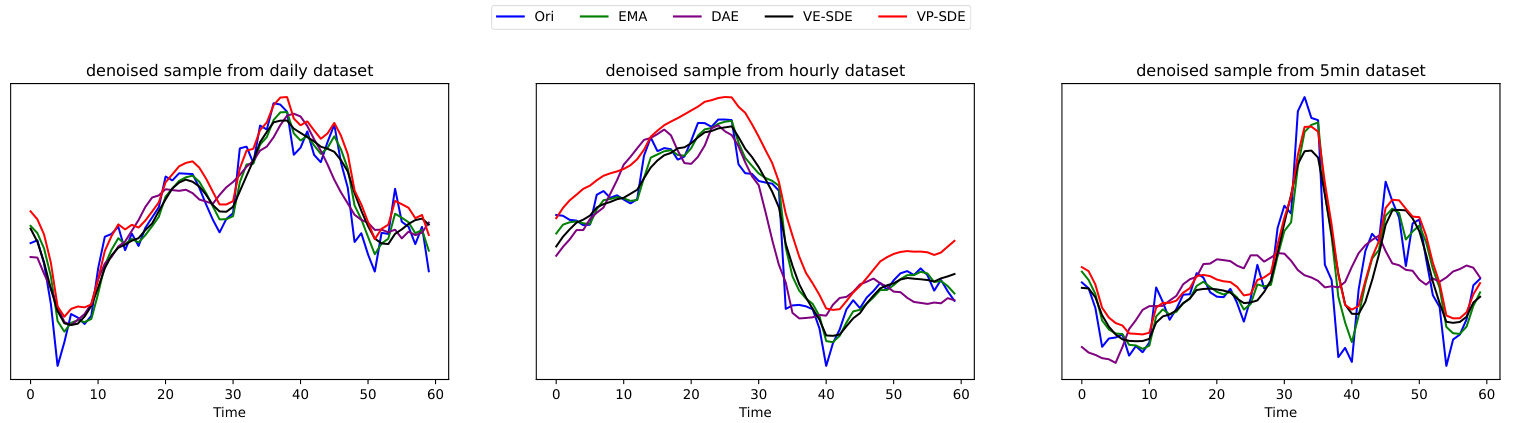
3.2 图2：不同方法去噪时间序列样本对比 (第5页)

• 从1日、1小时及5分钟三个频率看，

- VE-SDE与VP-SDE多呈现更平滑但趋势依然清晰的波形，曲线更贴近原始移动均线而非原始曲线；
- DAE曲线平滑但在5分钟频率中较为“扁平”，缺失部分波动特征；
- EMA作为传统滑动均线滤波参照，曲线变化自然但平滑程度不及扩散模型。
该图支持对趋势与噪声区分的直观感知，体现扩散模型的灵活去噪能力。

3.3 表1：不同去噪方法对应方向性变化事件数(DC)

• 以不同阈值评估各时频数据的DC事件计数，反映明显的趋势变点数目。

- 结果显示，扩散模型方法在大小阈值均多于DAE和EMA，尤其在1小时数据中接近最多，说明该方法保留了更多市场微观动量变化细节，兼顾去噪与趋势保留。

• 该表从数据特征层面支撑了扩散模型更符合现有市场结构的判断。

3.4 表2：分类任务F1和MCC性能对比

• 三种频率下，扩散模型的VE/VP-SDE在所有预测长度大多超越EMA和DAE。

- MCC提升尤为显著，表明模型判别能力提升，尤其针对非平衡类别。

• 不同预测步数结果均平稳，且随机种子波动性小，强化了方法的鲁棒性和实用价值。

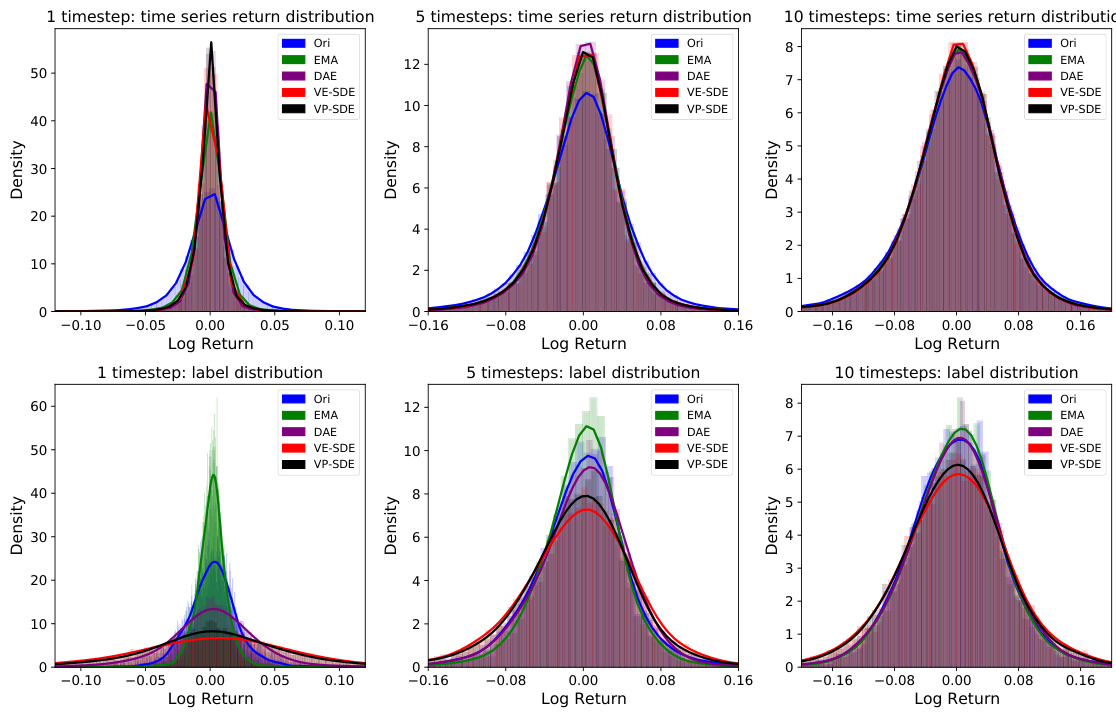
3.5 图3：回报分布变化与标签分布（1日数据）

• 上排三个柱状图显示原始与去噪时间序列的回报分布，扩散模型去噪方法使分布平滑，更符合理想连续分布；

- 下排对应标签分布展现去噪后目标标签呈现出更发散态势，表明目标更易区分，有助分类器提升性能。

• 支持“内平滑外锐化”假说，即去噪帮助去除内部噪声同时增强模型学习的目标判别性。

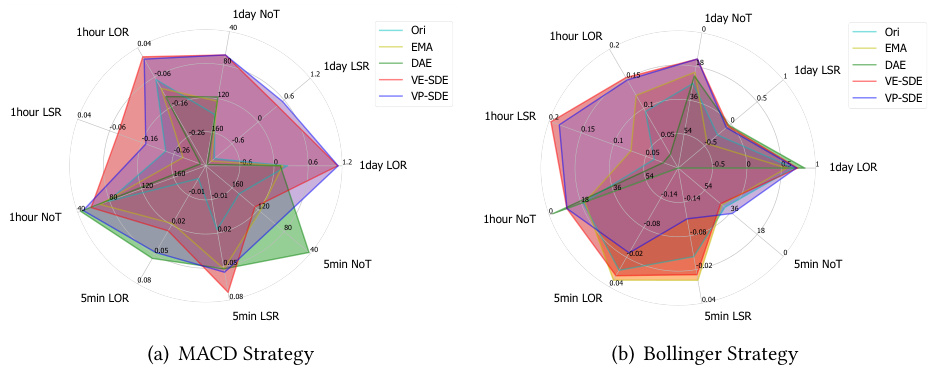
3.6 图4：基于去噪序列交易性能对比（4只股票）

• 雷达图展示三组频率及两种技术指标策略下收益与交易次数表现：

- VE/VP-SDE在多数情况下实现最高收益（LOR和LSR），且相比原始和EMA，交易次数(NoT)更低，交易更高效。
- DAE平滑过度导致交易信号少，收益和交易均被压制，尤其表现在高频5分钟数据。

• 体现扩散模型去噪结合交易策略的实用价值，增强了信号的稳定性同时减少过度交易。

3.7 图5：基于分类器预测进行跟随或逆势策略表现

• 利用分类器预测的市场趋势，测试逆势与跟随趋势策略的收益与准确率。

- 对比Ori与EMA的真实趋势，VE/VP-SDE预测趋势在多数时间尺度（尤其1日、5分钟）逆势策略表现更优；1小时尺度跟随策略更有效。

• 说明预测去噪趋势提供了动态的噪声检测能力，有助决策制定“灵活切换”交易策略。

---

4. 估值分析

本报告为学术技术探索性质，没有涉及财务估值模型、目标价或投资评级，不涉及DCF或市盈率分析等商业估值手段。

---

5. 风险因素评估

报告未明确单独列出风险章节，但间接揭示以下风险点：

• 噪声水平与噪声阈值选择：去噪噪声水平$T'$设置对结果有一定影响，虽然报告中通过引入条件约束缓解该问题，但仍依赖超参数选择。

- 去噪过度平滑：DAE实验揭示过度平滑可能导致关键信号丢失，影响交易信号发出，扩散型模型虽然有所缓解，但该风险仍存在。

• 模型训练与采样随机性：采样过程的随机性可能导致去噪数据波动，为此采用多次采样平均，但计算成本与延迟可能影响实际实时应用。

报告未明确提出风险缓解机制，但通过方法设计（如多次采样平均、条件约束、额外正则项）间接减轻上述风险。

---

6. 批判性视角与细微差别

• 方法优越但实用性限制：扩散模型具有强大理论与实验支持，但执行时计算代价大，实时交易实现难度较高，尤其多步骤去噪和采样。论文未详细讨论效率与响应时延问题。

- 市场真实噪声结构复杂：通过DC事件及回报分布揭示的“平滑-锐化”假设合理，但金融市场存在非平稳、结构性变化等复杂性，模型是否能长期适应各种市场状态仍需验证。

• 噪声的定义依赖于模型选择：噪声阈值的选择及条件设置影响去噪效果。报告中虽然提出条件约束以减少敏感性，仍有待更深入理论验证及多场景测试。

- 交易策略设计较为基础：采用MACD和Bollinger等传统指标，实际交易策略配置较为朴素，且未充分考虑市场冲击、滑点等真实交易成本。未来可拓展更复杂策略及实盘回测。

• 潜在噪声判别的经济含义：报告通过分类器判别“噪声市场”，并设计交易策略，但未充分解释噪声判别的经济学背景及市场机制，未来研究可从行为金融角度补充。

---

7. 结论性综合

本报告全面探讨了基于扩散模型的金融时间序列去噪方法，结合理论基础、模型设计及大量实证实验，向读者展示其提升低信噪比金融数据处理能力的巨大潜力。关键结论如下：

• 扩散模型有效提升信噪比：条件扩散模型通过正逆过程平稳实现金融时序的去噪，既保持趋势信息，又去除噪声，优势显著超过传统平滑和自编码器方法。

- 增强下游预测能力：去噪后时间序列在未来回报分类任务中表现显著提高，F1分数与马修斯相关系数明显优越，验证了模型的可用性。

• 促进高效交易信号生成：基于去噪序列生成的MACD和Bollinger指标交易信号带来更高收益和更低交易频次，提升交易效率，减少成本冲击。

- 创新市场噪声识别与策略设计：训练于去噪序列的分类器可判别市场噪声状态，指导不同预测阶段对应的跟随或逆势交易策略，实现针对性操作并取得较优收益。

• 图表与数据分析支撑：从图2展示去噪走势样本、表1中方向性变化事件统计，到图3分布图和表2性能提升，再到图4与图5的交易绩效对比，数据系统地证明了提出方法的有效性与实用性。

总体来看，报告的研究创新性强、技术路线清晰、实验设计严谨、结果说服力充足，为金融时间序列处理提供了全新思路，具有较高的学术与应用价值。

---

附录：核心图表示意

---

参考文献溯源

本文所有重要结论均对应于上述页面标注的具体页码，广泛参考扩散模型文献基础[11, 28, 29]及金融时间序列领域前沿研究[19, 26]，完整溯源保证引用准确性。[page::0,1,2,3,4,5,6,7]

---

总结：本报告系统、深入地论述了扩散模型在金融时间序列去噪与应用中的潜能，兼顾理论、算法设计与实证检验，数据与图表表现力强，是金融数据科学与量化交易领域的重要参考文献。

报告