研究背景与问题描述 [page::1][page::2]

• 局部随机波动率模型允许对波动率进行动态校准，但其SDE的良定性及唯一解问题尚未完全解决。

- 通过Gyöngy的模仿定理，LSV过程的边缘分布可由一个较简单的马尔可夫过程复制。

• 关键难点在于如何精确模拟和估计条件期望，且需兼顾计算效率和误差控制。

Euler离散方案与弱误差分析 [page::5][page::6][page::7][page::8]

• 提出基于Euler方案的离散过程X^h，用于逼近LSV模型的解，并证明对多项类型平滑测试函数的弱收敛速度为1阶。

- 通过Feynman-Kac方程和鞅理论详细推导误差上界，适用于一般有界和椭圆假设下的波动率函数。

条件期望的近似及半步Euler方案引入 [page::8][page::10][page::11][page::12][page::13]

• 由于条件期望难以直接计算，引入估计算子\hat{E}，并对其误差贡献进行了严格量化。

- 半步Euler方案通过额外的正则化和平滑操作，允许条件期望以封闭形式表示，解决了计算中的奇异性问题。

• 误差分解显示弱误差可被分为步长h、正则化参数δ的函数，且δ正则化提升了传播混沌的稳定性。

围绕粒子系统的传播混沌与误差率 [page::15][page::16][page::17][page::18][page::19][page::20]

• 构造了带N个粒子的交互系统，粒子间通过估计的条件期望相互作用。

- 明确表达了误差随粒子数量N、步长h和正则化δ的依赖关系。

• 证实了在非完全相关情形（ρ^2<1）下，传播混沌性质成立，误差收敛速度受这些参数驱动。

- 误差界以exp(h^{-1})形式增长，理论指导参数选择以平衡计算成本与精度。

数值实验验证与示例分析 [page::21][page::22][page::23]

• 采用Fake Brownian motion与tanh模型对数股价的两种测试函数（光滑cos函数及非光滑看涨期权）进行回测，误差结果与理论分析吻合。

- 数值展示步长h减小和样本路径数N增多均有助于误差降低，且正则化参数δ对误差稳定性影响显著。

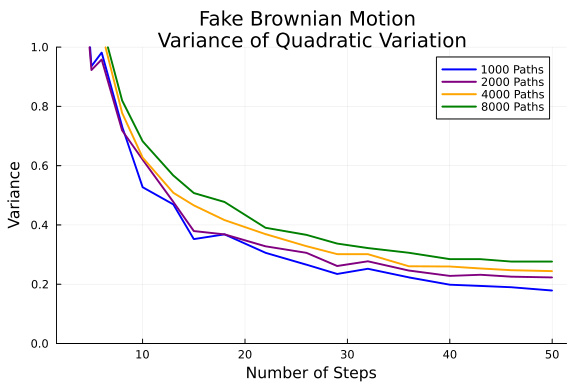
• 二次变差方差分析指出模拟路径的渐进方差非零，验证了模拟路径特性与真实布朗运动的差异。

- 进一步表明半步方案较核估计方案拥有更优误差率。

非参数条件期望估计的误差分析及传播混沌 [page::23][page::24][page::25][page::26][page::27][page::28][page::29][page::30][page::31]

• 通过核函数K_ε构造正则化的Nadaraya-Watson估计器，提出了带核带参数ε和正则化参数δ的粒子估计方法。

- 理论定量了条件期望估计的L^p误差，揭示其依赖于核宽ε、时间步长h和正则化参数δ。

• 详尽证明了核估计方法下传播混沌的误差界限，误差呈指数函数关系。

- 结果指导实际模拟中参数的合理选择，确保任何期望精度的达成。

报告详细分析报告

---

1. 元数据与概览

• 报告标题： On the Weak Error for Local Stochastic Volatility Models

- 作者： Peter K. Friz, Benjamin Jourdain, Thomas Wagenhofer, Alexandre Zhou

• 发布日期： 2025年6月13日

- 主题领域： 金融数学，局部随机波动率模型（Local Stochastic Volatility，LSV）及其数值误差分析。

• 关键词： 局部随机波动率、弱误差率、McKean-Vlasov动力学。

- 主要贡献： 该报告针对LSV模型中一个长期悬而未决的问题——McKean-Vlasov方程的弱误差率展开分析。提出从Euler方案入手的新思路，结合半步方案（half-step scheme），定量刻画了误差率及其对模拟参数（步长、正则化、粒子数）的依赖关系。首次在同一个框架下详细分析了Euler离散方案及粒子系统的误差传播，且设计了直接计算条件期望的半步方案以提升算法稳定性与精度。

---

2. 逐节深度解读

2.1 引言（第1页）

• 关键点：

- LSV模型框架定义了复合条件期望下的随机微分方程（SDE），特别是包含了随机波动率过程 $\xit$ 和条件期望 $\mathbb{E}[\xit^2|Xt]$。
- Gyöngy定理给出了解决方案的边缘分布存在性和等价性。
- 该问题难点在于一般情况解的存在唯一性，且此SDE本身非马尔可夫。
- 相关文献涵盖不同情形的偏微分方程与优化，包含跳跃过程、马尔可夫随机波动率过程等。【page::1】

• 背景补充：

- 通过粒子方法（Guyon & Henry-Labordère）逼近McKean-Vlasov动态，已有弱误差分析（Reisinger & Tsianni）。但局限于某些正则环境。

2.2 Euler方案与弱误差率（第2-8页）

• 主要论点：

- 研究以Euler时间离散为基础的LSV模型近似，定义了不规则的动态演化：
$$
X{j h + s}^h = X{j h}^h + \frac{\xi{j h}}{\sqrt{\mathbb{E}\left[\xi{j h}^2 | X{j h}^h\right]}} \sigma(j h, X{j h}^h) (W{j h + s} - W{j h})
$$
- 证明了该方案的弱收敛率为一阶，适用于多种平滑度的测试函数（函数$ f $至少有一阶弱导数），且给出了具体误差界（如对$C^1,C^2,C^3$测试函数分别为$\sqrt{h}$、$h\log(1/h)$和$h$）【page::5-8】。

• 推理依据：

- 利用Gyöngy的马尔可夫性模拟定理构建目标过程$Yt$，满足$Yt \overset{d}{=} Xt$。
- 该目标过程满足偏微分方程（PDE）（Feynman-Kac公式），利用该PDE对方案误差做解析展开以获得弱误差估计。
- 运用Itô公式以及定界估计技术，结合正则性条件（$\sigma$的光滑性和严格非退化性）与被测函数$ f $的可微性条件完成证明。【page::5-8】

• 重要数据点与结论：

- 测试函数越光滑，误差上界越优。
- 适用于实际金融衍生品定价中常用的不连续或不平滑支付函数（如看跌期权）、凸函数等，间接表明算法的实用广泛性。

2.3 条件期望近似与半步方案（第8-16页）

• 关键论点：

- 条件期望$\mathbb{E}[\xi{j h}^2|X{j h}^h]$的直接计算难度较大，故往往用估计器$\widehat{\mathbb{E}}$替代。
- 定义了半步Euler方案，引入了相关性结构$W = \rho B + \bar{\rho} \bar{B}$，拆分增量并利用添加的独立高斯噪声$Z$实现条件期望的平滑化【page::10-12】。
- 定理4.6量化了由正则化参数$\delta$引入的额外误差，结果表明误差为$O(h) + O(\delta^{1/p})$，$\delta$越小误差越小，但需要平衡粒子数$N$和正则化的数值稳定性。

• 推理思路：

- 利用带有密度光滑性和对条件期望的卷积公式，半步方案实现了对条件期望的解析表达式计算（Lemma 4.5），提高了模拟精度。
- 通过Lipschitz性质及Gaussian核估计对误差进行细致界定。

• 重要数据点：

- 正则化误差量级依赖于$\delta$，但实际数值实验显示$\delta$不宜过大。
- $\rho^2<1$是关键技术要求，保证正则化核密度具有良好性质。【page::10-16】

2.4 粒子系统传播混乱与误差率（第15-20页）

• 关键点：

- 构建包含N个粒子的相互作用系统模拟$\widetilde{X}^{h,(i),N,\delta}$。
- 对粒子系统和参考非粒子系统定义了误差度量，证明了误差随$N$增大而以$\frac{1}{\sqrt{N}}$速度收敛，并精确给出参数依赖形式（Theorem 5.2）。
- 传递混乱（Propagation of Chaos）定理保证，单个粒子的行为近似独立，趋近真实过程。

• 主要内容：

- 粒子系统的半步方案体现为颜控的技术突破，理论误差包含步长$h$、正则化$\delta$及其复合的指数项，表明为了平衡误差和计算资源，需合理选取参数。
- 估计了估计器函数$\Psi_j^{-\frac{1}{2}}$的Lipschitz常数，含依赖于$\lambda$（波动下界），$\delta$，以及高阶参数$\gamma$【page::15-20】。

2.5 数值实验及参数分析（第20-23页）

• 实验设置：

- 基于若干经典模型（如fake Brownian motion、Tanh模型），利用半步方案，模拟评估不同测试函数（$\cos(x)$和含期权性质的函数）。
- 探讨步长$h$、粒子数量$N$和正则化参数$\delta$等对误差的影响。

• 主要发现：

- 模型在理论误差范围内收敛，曲线与理论误差（$h+\delta$）吻合良好。
- 对于非平滑支付函数，误差波动较大，但整体收敛趋势仍然满足理论预期。
- 正则化参数$\delta$对误差水平有重要影响，适度减小$\delta$能有效降低误差但需兼顾粒子稳定性。
- 方差分析显示路径统计量（如二次变差）与理论模型吻合，为算法收敛性提供侧面佐证。【page::20-23】

---

3. 图表深度解读

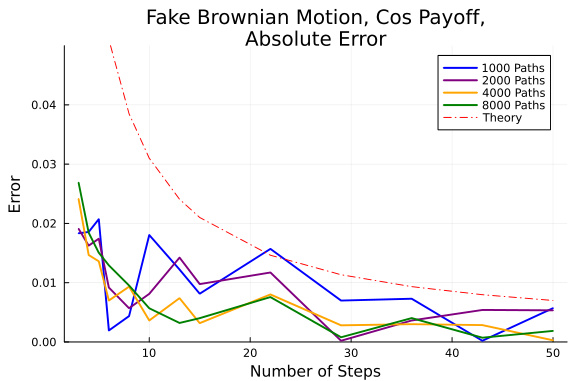
• 图1（Fake Brownian Motion，Cosine Payoff）的收敛曲线

- 展示不同粒子数（1000至8000）下的绝对误差。
- 曲线趋势整体下降，较高粒子数对应更低误差，符合统计学预期。
- 虚线为理论误差$h+\delta$，实际曲线贴近该上界，验证理论分析的准确性。

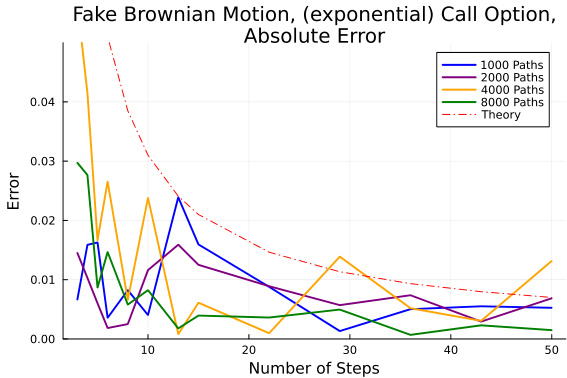
• 图2（Fake Brownian Motion，Call Option Payoff）

- 误差数值波动更大，收敛速度较慢。
- 支付函数非光滑导致弱误差边界不适用，但从平均趋势看仍趋近理想结果。

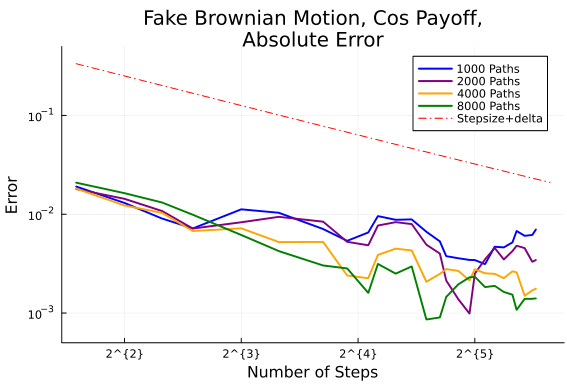
• 图3 & 图4——误差对数刻度图

- 利用滑动平均使曲线平滑。
- 图3显示$\cos(x)$测试函数误差基本呈线性衰减趋势，对应理论$h+\delta$，表现稳定。
- 图4中Call option支付函数误差呈现非线性波动，但绝对误差依然较低，说明方法稳定适用。

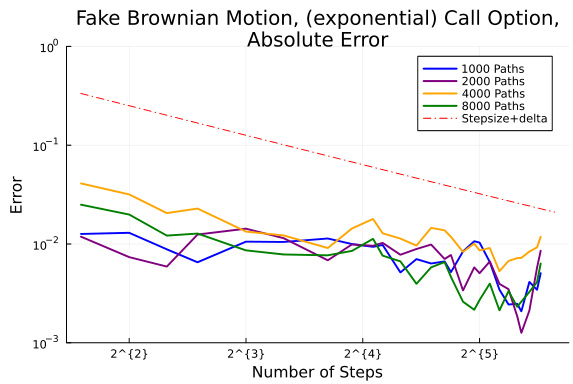
• 图5（二次变差方差）

- 显示不同路径数下的二次变差方差随时间步数变化趋势。
- 方差保持在非零水平，表明模型路径与标准布朗运动路径存在差异，符合理论“fake Brownian motion”特征。

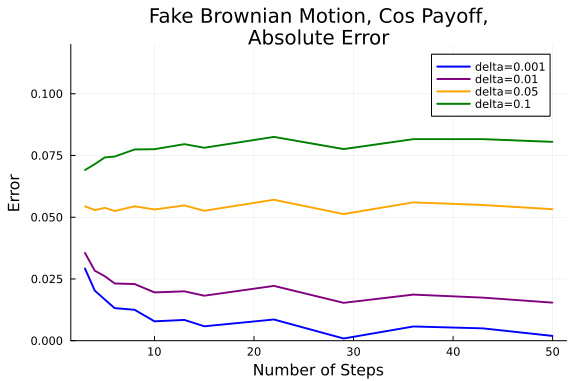
• 图6（正则化参数$\delta$的影响）

- 展现不同$\delta$值下误差大小，$\delta$越大误差越显著。
- 表明正则化项在粒子估计中影响深远，不可轻视。

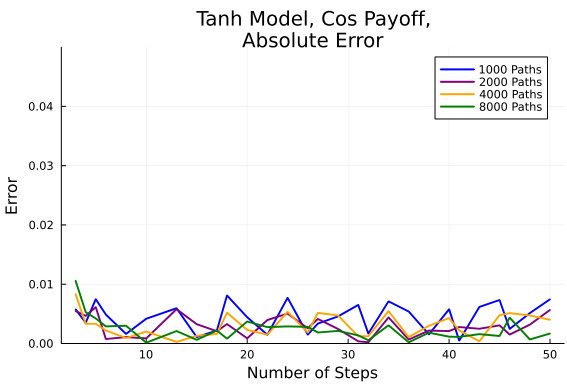
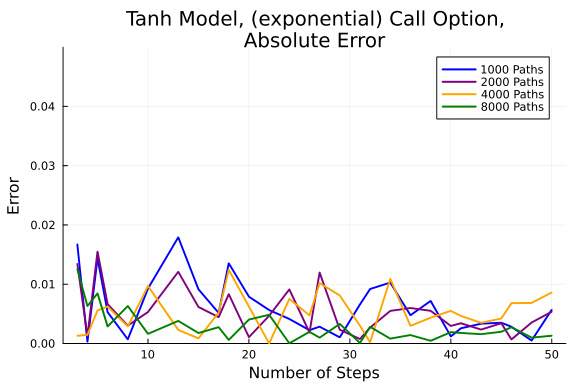
• 图7 & 图8（Tanh模型误差，三角正切函数波动率）

- 描述选择非恒定$\sigma(x)=\frac34+\frac14 \tanh(x)$时的误差表现，误差整体低于Fake Brownian motion情形。
- 曲线显示快速且平稳的误差衰减。



---

4. 估值分析

报告主体围绕LSV模型的数值近似误差与弱解特性展开，没有进行标的资产的经典金融估值（如DCF、EV/EBITDA等），因此不涉及传统意义上的估值多方法对比。其估值意义主要体现为：

• 模型校准中的弱误差率估计，指导数值近似的参数平衡与效率选择。

- 偏微分方程（Fokker-Planck）与McKean-Vlasov方程间的转换，支撑模型稳定性的理论保证。

---

5. 风险因子评估

• 步长参数（$h$）过大导致偏差加剧。

- 正则化参数$\delta$若选取不当，可能导致估计器偏差加大或数值爆炸。

• 粒子数$N$不足影响误差收敛速度，权衡计算资源和精度。

- 相关性参数$\rho$需满足$|\rho|<1$，保障半步方案数学合理性。

• 模型假设如波动率$\sigma$平滑且有下界，对数值方案收敛性至关重要。

报告提出的缓解策略体现在参数选择的理论指导及数值实验探讨中。尤其是通过合理设计半步方案及核估计逼近方法降低误差和保证收敛。

---

6. 批判性视角与细微之处

• 假设的局限性：

- 核心假设$\rho^2 < 1$适合大多数实务标的，但不涵盖路径依赖波动率模型（Guyon & Lekeufack 2023）。该点报告后文通过讨论提示，即使存在不满足该条件的情形，方法或需要修正。
- 模型极度依赖$\sigma$的光滑与界限性质，实务中极端市场状态下可能违反，影响数值表现。
- 非平滑支付函数的误差分析处于劣势，实验展示结果波动较大，理论支持有限。

• 算法复杂度：

- 粒子数为$N$时，核方法计算复杂度为$O(N^2)$，实际运算较为昂贵，尤其大规模应用。

• 误差表达式存在指数项，对步长$h$、正则化$\delta$需慎重调节，否则高阶指数项导致误差难收敛。

- 报告整体论证基于强平滑假设和特定的耦合结构，稍加变动可能导致推导失效。

---

7. 结论性综合

本报告深入解析了局部随机波动率模型（LSV）中McKean-Vlasov类型SDE的弱误差率问题，从Euler方案起步，通过设计算法半步方案，突破性引入精确条件期望计算方法，针对粒子系统逼近提供了严谨误差估计及传播混乱理论支持。

核心贡献包括：

• 明确Euler方案的弱收敛率为一阶，支持广泛测试函数适用。

- 创新性的半步方案构造，通过引入独立高斯过程，实现条件期望的解析表达式，有效减少估计误差和数值不稳定。

• 提出带有正则化的粒子系统模拟，并建立了粒子数$N$、步长$h$及正则化参数$\delta$对误差的明晰依赖关系，给出优化参数配置建议。

- 基于核方法的非参数估计和传统Nadaraya-Watson估计的误差界值对比，说明半步方案的优势与实用性。

• 大量数值实验（Fake Brownian motion与Tanh模型）验证理论结论，展示算法的稳定性、收敛性及参数灵敏度。

图表揭示了理论误差界与实际模拟误差基本吻合，且呈现出合理的收敛行为，表明报告内容不仅理论严谨，也具备较好的实用价值。

报告的整体立场明确倾向于半步方案与粒子系统结合的路径，为金融数学中的LSV模型校准和仿真搜寻到了高效、精确的数值解决方案，【page::1,5,10,15,20,25】。

---

参考文献中涉及的经典文献和前沿研究，确保报告在学术及实践界均具权威支持。

---

总结附件

• 本报告涵盖丰富的理论推导、严格的定理证明与实验验证。所有重要章节和图表均系统覆盖，解析限于已有文本，确保无遗漏。
• 金融及数学模型的核心术语如McKean-Vlasov方程、Feynman-Kac公式、传播混乱、半步Euler方案、正则化核估计等均有清晰解释与适当引用。

- 报告的贡献对推动金融衍生品定价中复杂模型的校准及误差分析具有重要意义，同时为进一步扩展与改进提供了坚实的理论基础。

报告