• 研究背景与问题：2023年硅谷银行等美国及瑞士银行倒闭凸显银行间传染风险，传染渠道分为系统性（全局因素驱动）与特有性（银行间影响）两类。研究目的是辨别这两种风险传染类型及其动态演变 [page::1][page::2]。

• 模型方法：提出多因子copula、结构化因子copula（bi-factor及nested-factor），以及因子藤蔓copula模型，结合潜变量和双变量copula描述银行间复杂非线性尾部依赖关系。采用变分贝叶斯推断提高估计效率并支持模型自动选择，并捕捉未知双变量copula族 [page::3][page::6][page::9][page::10][page::11]。

• 数据与样本：选取2007年至2023年欧洲8家及美国7家主要银行的5年期CDS日数据，涵盖2008金融危机、欧洲债务危机、新冠疫情、2022年利率飙升及2023年银行倒闭等多重历史压力测试期。对CDS数据进行了对数差分处理并建模波动（AR-GJR-GARCH模型），转化为均匀分布作为copula建模输入 [page::11][page::12][page::13][page::14]。

• 模型拟合与比较：对美国、欧洲及两地区联动分别用五种模型拟合，BIC显示区域内最优为因子藤蔓copula，联合样本的最优模型为bi-factor copula，表明区域内同时存在系统性和特有性传染，但跨境体系以系统性传染为主 [page::15][page::16]。

| 模型类型 | 美国银行BIC (全样本) | 欧洲银行BIC (全样本) | 联合样本BIC (全样本) |
|----------|----------------------|----------------------|---------------------|
| One-factor | -22622.88 | -30878.72 | -41131.21 |
| Two-factor | -22610.04 | -32215.13 | -54773.96 |
| Bi-factor | N/A | N/A | -56212.63 |
| Nested-factor | N/A | N/A | -54336.74 |
| Factor-vine | -22698.24 | -32670.12 | -53731.25 |

• 因子藤蔓copula分析：第一层因子-银行对多为t-copula，表现尾部肥厚且对称；第二层银行间连接的copula模型类型多样，且随时间变动明显。美国银行系统中，银行依赖结构时变性强；欧洲银行系统结构较为稳定且联系紧密 [page::16][page::17].

• 预测检验：采用滚动样本20日步长滚动预测及负对数似然(LPS)、条件似然(CdL)和变差评分(VarS)等指标评价。区域内因子藤蔓copula预测表现最佳，联合样本则以bi-factor模型领先，表明跨区域系统性因子主导。上尾风险分析显示区域内多因子系统性传染表现突出，联合模型中兼具系统性及特有传染特征 [page::18].

- 系统性风险指标预测：基于最佳拟合模型（联合样本采用bi-factor copula）模拟未来20日CDS数据，计算个体违约概率（PD）、联合违约概率（JPD）、条件违约比例期望（EPD）及条件预期损失（ES）。模型成功识别了2020新冠疫情、2022利率飙升及2023银行倒闭期间风险急剧上升，且反映了不同银行系统性影响力和脆弱性，如Credit Suisse和Goldman Sachs尤为突出 [page::19][page::20][page::21][page::22].

• 结论摘要：本研究定量区分并建模银行系统金融传染的系统性与特有性渠道，提出的因子藤蔓copula及结构化因子copula模型结合变分贝叶斯实现高效估计。区域层面系统性与特有性传染并存，跨境层面传染以系统性为主。系统性风险预测准确对应历史危机阶段，对监管与风险管理具有重要参考价值 [page::22].

金融研究报告详尽分析报告

1. 元数据与报告概览

报告标题： Structured factor copulas for modeling the systemic risk of European and United States banks
作者： Hoang Nguyen, Audrone Virbickaite, M. Concepción Ausín, Pedro Galeano
发布机构： 瑞典林雪平大学管理与工程系、西班牙CUNEF大学定量方法系、西班牙卡洛斯三世大学统计学系与Santander大数据研究所
发布日期： 2024年1月9日
研究主题： 利用结构化因子copula模型，基于欧、美银行的信用违约掉期（CDS）数据，建模和分析系统性风险和金融传染效应。

核心论点及目标：
本报告旨在通过多因子、结构化因子和因子vine copula模型，揭示欧盟和美国银行间的违约相关性及其内部的系统性与特定银行间传染机制。报告使用CDS市场数据，建构基于因子copula的联合与条件违约概率模型，识别系统性（全球及区域因子）和特定银行间（非系统性）传染渠道。通过模型拟合与预测，回顾并解释近年来银行业多次危机期间的风险爆发，凸显全球金融传染的主要驱动因素。最终，报告推荐了对银行系统风险测算更有效的copula模型架构，并提出了基于Variational Bayesian方法的模型估计和选择新方案。[page::0,1,3,15,22]

---

2. 逐章深度解读

2.1 引言（第1章）

报告首先强调金融机构间复杂的相关依赖结构在2008年全球金融危机后重要性提升，2023年又因几家区域性银行（硅谷银行、Signature银行、First Republic）及欧洲的瑞信银行的倒闭，激化了对金融传染现象的研究关注。金融传染定义为局部冲击导致整个系统性风险扩散的效应。

作者指出传染源一般分为两类：

• 系统性传染（global/systematic）： 由全球性或跨国因素驱动，如宏观经济波动等，具共通性。

- 特定银行传染（idiosyncratic/local）： 由个别金融机构间直接联系或暴露导致，强调机构间直接风险扩散。

报告提出的问题是捕捉和区分两者的复杂依赖关系，并明确两者在不同时期的主导作用。同时，现实数据的因子结构复杂、多因子存在，且依赖关系非线性、高维、非高斯。对此，作者提出基于因子copula和因子vine copula方法，灵活刻画条件和联合违约风险，突破维度和模型选择的技术困境。[page::1,2]

---

2.2 图示解析：系统性与特定银行传染机制（图表1，第2页）

图1形象说明两种传染渠道：

• 左图：单个潜变量\( F \)影响所有银行\( Bi \)，体现系统性、跨国共振效应。

- 右图：单个银行\( B1 \)直接影响其他银行，表明特定银行风险传染。

此图辅助理解copula模型中潜因子与观测银行间关系的数学刻画。报告指出实际中两者并存，强度随时间波动。并且数据的高维和非标准分布需用灵活且低参数模型处理。[page::2]

---

2.3 相关文献综述（第2章）

报告回顾了相关领域用copula方法建模金融传染的文献，包括：

• 跨地区股票市场和主权信用风险传染（Rodriguez, 2007；Aloui et al., 2011）

- 利用vine copula分析银行间风险以及尾部依赖（Brechmann et al., 2013；Kleinow and Moreira, 2016）

• 利用时间变动copula计量信用风险及系统性风险（Oh and Patton, 2018；Krupskii and Joe, 2020）

本报告在此基础上提出结构化和vine拓扑结合的因子copula模型，引入新的高效估计与模型选择方法，扩大适应范围和深度。[page::3,4]

---

2.4 模型详述（第3章）

2.4.1 CDS与隐含违约概率转换（3.1节）

采用简化的CDS定价模型，将CDS点差\(S\)转化为隐含风险中性违约概率\(p\)（假设固定利率\(r\)、固定违约损失率\(L=75\%\)），通过贴现现金流平衡计算，近似关系为：
\[
S \approx pL
\]
为实证需要，原始点差进行对数差分处理、用AR-GJR-GARCH模型拟合带有偏斜t分布的残差，保证序列稳定性和捕捉尾部肥厚、不对称性等特征。

此外说明各模型设定差异及合理性验证，利用概率积分变换将残差转换为[0,1]的均匀分布，为后续copula建模做准备。[page::4,5]

2.4.2 Copula基础与多因子模型（3.2及3.2.1节）

基于Sklar定理，联合分布通过copula分解为边际分布与依赖结构。报告选择因子copula架构（Krupskii and Joe, 2013）规避高维参数爆炸问题，构建多层C-vine结构。
单因子copula中，观测变量\(Ui\)条件独立，依赖潜变量\(V0\)。多因子模型中添加多个潜变量\(Vj\)，形成二层甚至更复杂模式。通过边际及条件分布推进计算条件copula密度及整体密度积分，虽积分维度增加但仍能控制参数复杂度。图2直观展示单因子与双因子copula意味着因子与变量的连接方式。[page::6,7]

2.4.3 结构化因子模型（3.2.2节）

为应对更复杂关联和“维度诅咒”，引入基于分组的结构化因子模型（Krupskii and Joe, 2015），其中银行按区域或其他标准划分为\(G\)组，\(G+1\)个潜因子包括总体潜因子\(V0\)与组级潜因子\(Vg\)。
两大类型：

• Bi-factor模型：观测变量条件独立于潜因子，且各组独立给定公共潜因子。

- Nested-factor模型：组潜因子\(Vg\)本身依赖于公共潜因子\(V0\)，产生层次化依赖结构。

图3给出示意，显著提升模型灵活性同时兼顾复杂关联结构。[page::7,8]

2.4.4 因子vine copula（3.2.3节）

进一步引入因子vine copula（Nguyen, 2019），结合因子copula和截断式vine copula，允许在潜变量支配的第一树分支捕获系统性依赖，同时高层vine捕捉残余的金融机构间非系统性关联和尾部非对称性。

模型由一系列树形结构组成，第一棵树（\(T0\)）连接潜变量\(V0\)，后续树由上一树的边构成节点，树间符合特定结构约束。图4显示一个两级截断因子vine结构实例。此结构既解释经济学含义也弥补传统因子copula对非高斯尾部依赖的不足。[page::8,9]

---

2.5 贝叶斯推断与参数估计（第4章）

针对高度复杂的结构化因子copula模型，传统MLE估计因参数固定限定和计算负担难以灵活选择copula族而受限。报告引入Variational Bayesian（VB）推断近似技术，对模型隐含潜因子和copula参数进行快速估计。其核心为：

• 设定潜变量\(v{0,t}\)与copula参数的先验（潜变量为均匀，copula参数保持Kendall \(\tau\)限制在[-0.9,0.9]）。

- 构造后验分布（形式复杂，含大量积分）

• 利用黑盒变分推断，通过最大化ELBO转为优化问题，使用Monte Carlo采样估计梯度，进而求解参数近似后验。

这种VB方法速度较MCMC快，精度略有折中。
且报告研发自动化copula族选择机制，通过交替估计潜因子与bivariate Copula模型，基于BIC准则调整连接copula类型，提升模型灵活性和适合度。对vine结构按层选取copula族，实现分层模型自适应构建。[page::9-11]

---

2.6 实证说明

2.6.1 数据预处理（5.1节）

选取2007年1月1日至2023年5月1日间，日频5年期CDS残值数据，涉及8家欧洲银行与7家美国银行（如表1）。为保证数据质量，部分缺失数据进行插补处理。数据时长超过16年，涵盖2008金融危机、欧洲债务危机、COVID-19等重要事件，显著适合长期违约风险建模。
图5清晰展现CDS与隐含违约概率的时序波动，显示事件期间压力峰值，凸显研究主题的现实意义。最大CDS点差高达1360bps（摩根士丹利，2008）和1082bps（Credit Suisse，2023）。区域间风险传递可从宏观趋势反映出明显差异。[page::11-13]

2.6.2 边际模型拟合（5.2节）

根据对数差分CDS点差序列的描述统计与波动聚集特征，拟合AR(4)-GJR-GARCH(1,1)模型带偏斜t分布误差。
分析显示：

• 大多数银行存在正偏的AR前阶系数与负偏后阶效应，反映波动集聚与杠杆效应，且波动有明显非对称响应（负震动降低未来波动，因波动为CDS利差变动）。

- 残差分布极度胖尾，模型拟合后，利用概率积分变换后数据满足均匀分布假设，有效满足后续copula要求。
相关分析（图7）显示区域内银行间高度正相关，尤其欧洲银行相关性显著高于美国银行，暗示区域金融网络紧密度差异。[page::13-15]

2.6.3 模型拟合优度分析（5.3节）

尝试多种copula结构模型：单因子、双因子、bi-factor、nested-factor及因子vine copula，用BIC指标评估拟合优度（表3）。

• 对美国与欧洲单一区域，因子vine copula普遍优于其他模型，说明区域内系统性和特定银行传染两渠道并存。

- 尤其在疫情及疫情后期美国银行（2020-2023）阶段例外，单因子模式最佳，表明当期共同风险因子占主导。

• 跨区域联合考虑时，bi-factor模型最佳，表明全球共有潜因子及两片区独立潜因子驱动风险扩散，而银行间直接互传染影响微弱。

进一步结构分析表明，连接潜因子的因子-unit关系多为\( t \) copula（脂尾对称依赖），而因子vine第二层单位-unit边间copula多样（弗兰克、Gumbel等），表明系统内尾部依赖及非对称性由非系统性因素捕获。图8展示了不同子样本下各银行间尾部依赖结构差异，欧洲网络结构更稳定，美国银行间联系变化较大。[page::15-17]

2.6.4 模型预测评估（5.4节）

采用滑动窗口方法对2019-2023年的最后1000条数据滚动预测，使用三类预测评分指标：

• 负对数预测评分（LPS）：评价整体预测分布拟合优度。

- 条件似然分数（CdL）：侧重高尾区域（极端风险）预测准确性。

• 变异函数评分（VarS）：评价预测的多变量联合行为。

结果（表4）显示：

• 在单一区域，因子vine模型预测综合表现最佳。

- 对全球区域联合，bi-factor模型预测表现最好。

• 然而从高尾CdL指标看，单一区域内双因子模型反映极端风险更为精准，体现单一区域内系多源系统性传染更显著；跨区域联合高尾风险则需要兼顾局内与局外传染渠道，因子vine模型表现优异。

综合来看，区域内更侧重双因子及vine模型，跨区域更多体现在系统性潜因子为主导。[page::17-19]

2.6.5 系统性风险测度及动态分析（5.5节）

基于模型模拟的联合违约概率，构建四类系统性风险指标：

• \(PDi\)：单个银行未来20天的违约概率

- \(JPDk\)：系统中至少\(k\)家银行违约的联合概率

• \(EPDi\)：假定银行\(i\)违约时，其他银行违约比例的条件期望

- \(ESi\)：系统中有多家银行违约时，银行\(i\)的预期CDS点差

图9展示上述指标在2019-2023年滚动预测结果：

• 2020年COVID-19疫情期间，所有银行个体违约概率及联合违约概率出现显著且普遍峰值，反映系统广泛风险扩散。

- 2022年及2023年初利率急剧上升与银行危机事件期同样呈现高风险波动，显示利率变化对银行风险敏感度较高。

• 个别银行如意大利的埃尔萨诺银行(Intesa Sanpaolo)在疫情期间的重要性指标\(EPD\)显著飙升，表明该银行违约对整体系统影响巨大。

- \(ES\)指标揭示不同银行在系统压力下的脆弱程度，如高盛在疫情期间曝露出高风险暴露。
整体分析显示所提模型和风险度量有效捕捉了历史危机中多层次系统风险的动态特征，具备较强的实用性与前瞻性。[page::19-22]

---

3. 图表与图像深度解读

3.1 图1：系统性与特定银行传染示意（第2页）

清晰区分系统性传染（由公共潜变量影响全局银行）和银行间特定传染（由单个银行向其他银行传导），为后续模型物理含义奠定基础。[page::2]

3.2 图2：多因子copula结构示意（第7页）

展示单因子copula和双因子copula的网络结构，直观表现潜因子如何根植于银行节点，为理解多因子模型中的因子依赖关系提供视觉辅助。[page::7]

3.3 图3：结构化因子copula结构示意（第8页）

通过bi-factor和nested-factor模型，描绘多组潜变量的依赖及层级结构，强调维度灾难缓解和群体间联系的动态表现。[page::8]

3.4 图4：截断因子vine copula示意（第9页）

结合因子模型和vine结构，图形说明分层依赖捕获不同依赖形式和尾部风险，利于解释系统性和银行间逾对称性尾部相关体。[page::9]

3.5 图5：CDS点差与违约概率动态（第13页）

上半部多条银个体CDS点差时序线性叠加，直观显示重大金融压力事件期间风险急剧上升；下半部对应由点差转换的隐含违约概率轨迹，确认风险水平随CDS同步波动，且历史低谷与高峰明确。反映了区域间不同危机期间风险传导特点，印证实证分析的归因逻辑。[page::13]

3.6 图6：CDS对数差分时序表现（第14页）

动态频繁剧烈波动，平均值均为正，表明整体上CDS风险高于初始水平。灰色为个别银行时间序列，黑色为平均趋势，展示个体差异和总体走势。[page::14]

3.7 图7：CDS对数差分关联矩阵（第15页）

灰度矩阵刻画欧洲和美国银行组内高相关性，组间关联较弱，体现区域属性对风险传染的影响，显示系统分层结构。[page::15]

3.8 图8：因子vine模型第二层详细结构（第17页）

展示两子样本期间，欧洲和美国银行间尾部依赖链路与copula族的变化。

• 美国银行网络结构变化明显，尾部依赖关系多样；

- 欧洲银行网络结构更稳定，尾部依赖保持一致。
展示了区域市场传染机制的时间异质性和风险网络演变。[page::17]

3.9 图9：主要系统性风险预警指标滚动预测（第21页）

四个三维图分别反映单个银行违约概率（PD）、多银行联合违约概率（JPD）、某银行违约时系统违约比例预期（EPD）和特定风险暴露（ES）。所有指标直观揭示了COVID-19及后续利率冲击引发的系统风险扩散，解释了历史重大事件中银行系统的脆弱性和相关性强烈性。[page::21]

---

4. 估值与方法评价

报告未直接进行估值（估价）分析，核心为风险建模与系统依赖测度，模型重点在于构建高维、复杂结构copula模型并有效推断联合违约概率，突出统计建模意义。估值技术主要体现为：

• 模型架构： 通过多因子、结构化因子与vine级联组合捕获金融机构关联性，避免模型维度爆炸和计算繁琐。

- 变分贝叶斯估计： 利用黑盒自动微分技术，实现对复杂后验的快速近似，用于高维模型结构选择与参数估计。

• 模型选择： 结合BIC与自动copula族识别，实现高效且灵活模型优化。

综合反映当前金融风险度量中因子依赖模型的先进估计与选择技术，兼顾理论和实证两方面需求。[page::9-11,16-18]

---

5. 风险因素评估

作者明确了两类风险传染渠道：

• 系统性风险： 全球及区域潜因子驱动，主导大范围同步违约风险，如2008年危机、2022年利率上升等。

- 特定机构风险： 机构间尾部依赖与传染，尤其区域金融系统内部如欧洲，表现更出色，有时在极端情况下单银行风险传染起重要作用（2023年个别美国银行危机明显体现此特征）。

报告动态评估发现，不同时间段系统性与特定风险角色权重变化，明确传染过程多渠道共存，且模型能识别并预测多种风险爆发期，对监管和风险管理提供实用洞察。[page::1-2,16-22]

---

6. 批判性视角与细微差别

• 模型假设及选择依赖：

尽管模型设计精巧，依赖于特定copula族选择及分组策略（如按地理划分），这种预分类可能限制捕获更复杂的关联结构，尤其是国际跨界连锁反应可能存在的动态变化。

• 尾部依赖假定：

主要因子-unit连接多为对称脂尾\(t\)型copula，但实际金融传染可能表现一定尾部非对称性，尽管vine层次部分捕获该异质性，模型整体是否充分刻画极端右尾风险存在讨论空间。

• 估计方法的局限：

变分贝叶斯方法虽快速，但报告也提示其可能低估参数不确定性，尤其尾部和极端事件建模中的置信区间可能偏窄。

• 数据样本与银行选择偏差：

若关键倒闭银行CDS数据缺失（如2023年三家美国银行），可能低估危机期间特定风险传染强度，对结果的全面性有一定影响。

• 模型动态演变考虑有限：

虽涉及滚动窗口估计，潜因子和结构动态变化的更复杂时间序列建模尚待深化。

整体报告结构严密、分析全面，缺点主要是模型对于异常极端情况的敏感度和动态复杂系统的微妙变化捕捉可以进一步加强。[page::1-2,15-18]

---

7. 结论性综合

本报告创新性地利用结构化多因子及因子vine copula模型，结合变分贝叶斯估计与自动化copula族选择技术，构建了多层次、多渠道的银行系统风险建模框架。该模型能够精准识别欧洲与美国银行系统内存在的系统性（潜因子驱动）与特定银行间（机构间）两大传染渠道，表明：

• 区域级别风险传染具有双渠道特征， 系统及机构间传染共存，风险层级丰富，尾部依赖表现多样。

- 跨区域全球系统传染以系统性潜因子为主导， 银行间直接风险传递较弱。

• 评估模型在历史重大金融事件（2008、欧洲债务危机、COVID-19、2022年利率冲击及2023年银行危机）中均有效捕获风险爆发期， 支持模型的实际监测和预测价值。

- 系统性风险度量指标（PD, JPD, EPD, ES）提供了多角度的风险透视， 有助于监管机构和市场参与者洞察风险来源及相对重要性。

报告细致结合丰富的数据与模型对比，验证模型广泛适用性，指出未来研究可关注动态模型演进、多样尾部依赖、跨区域复杂网络动态等，推动系统风险建模理论与实践进步。[page::22]

---

参考报告中关键图表展示

图1：系统性与特定银行传染结构示意

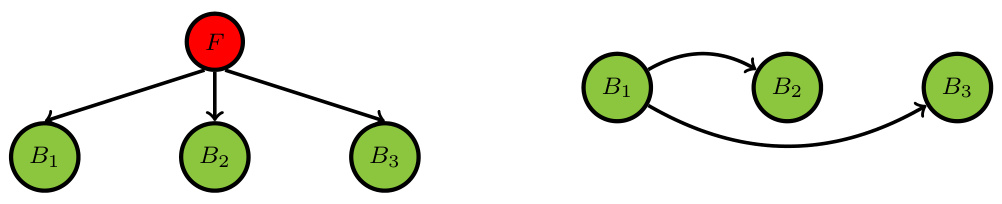
图2：多因子copula模型示意

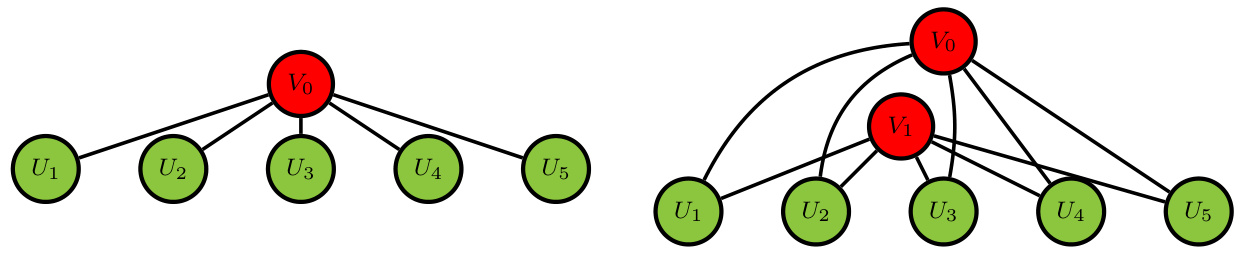
图3：结构化因子copula示意

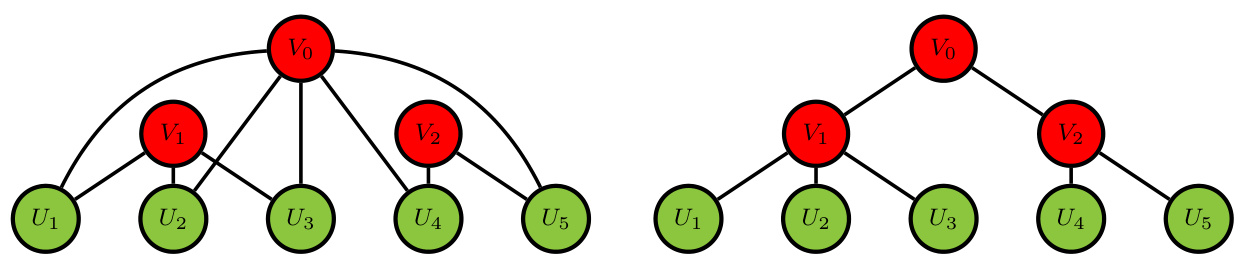
图4：因子vine copula示意

图5：CDS点差及隐含违约概率动态

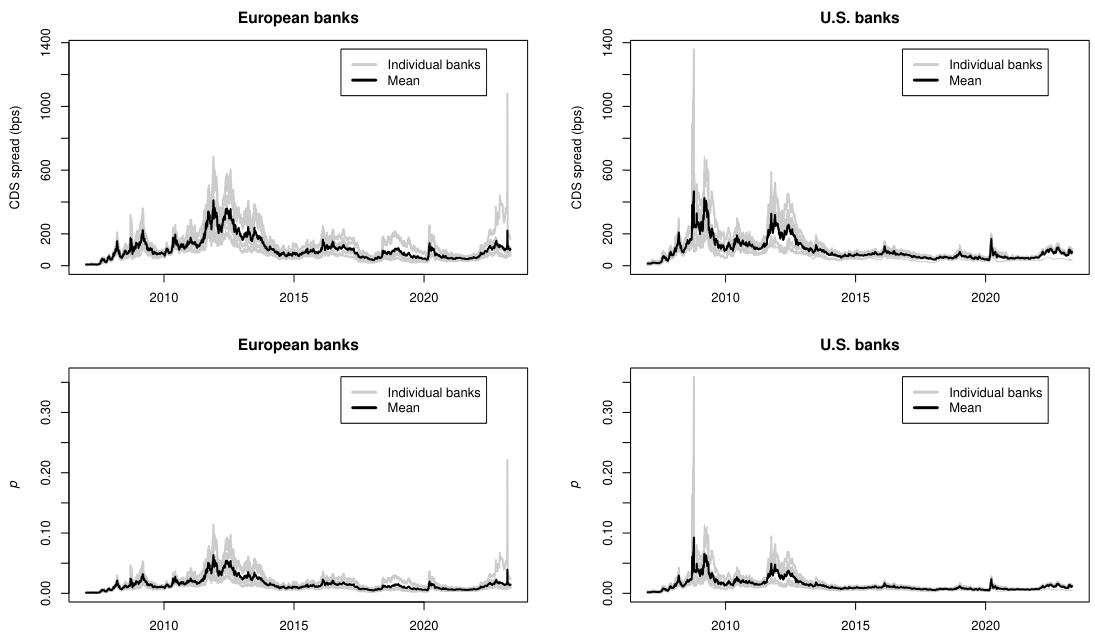
图6：CDS点差对数差分动态

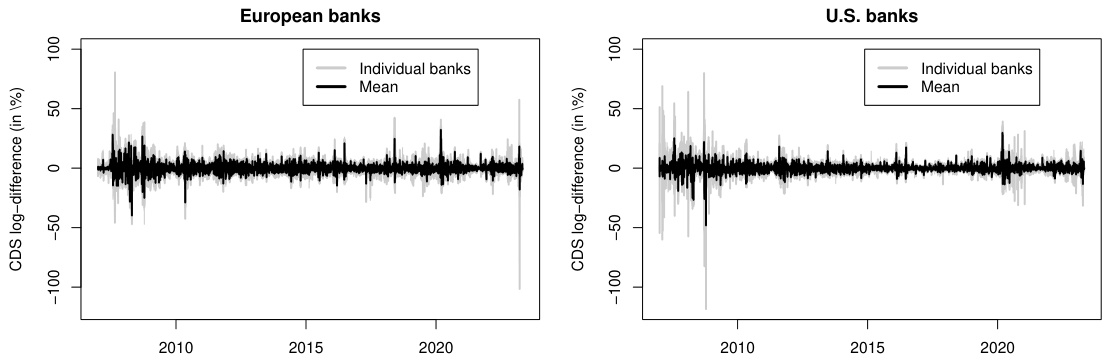
图7：CDS对数差分相关矩阵

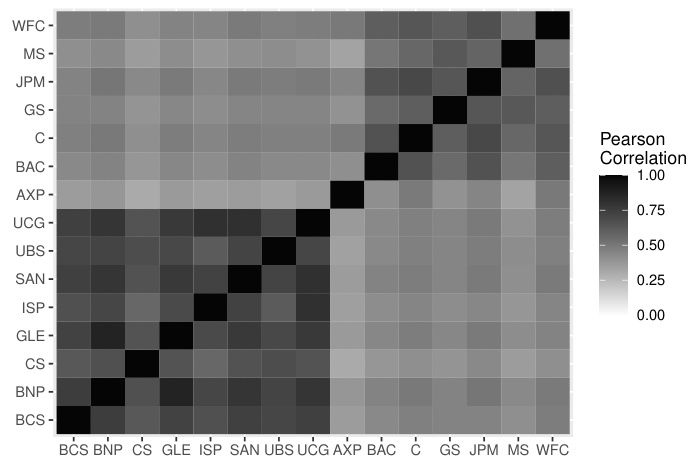
图8：因子vine模型第二树层依赖结构

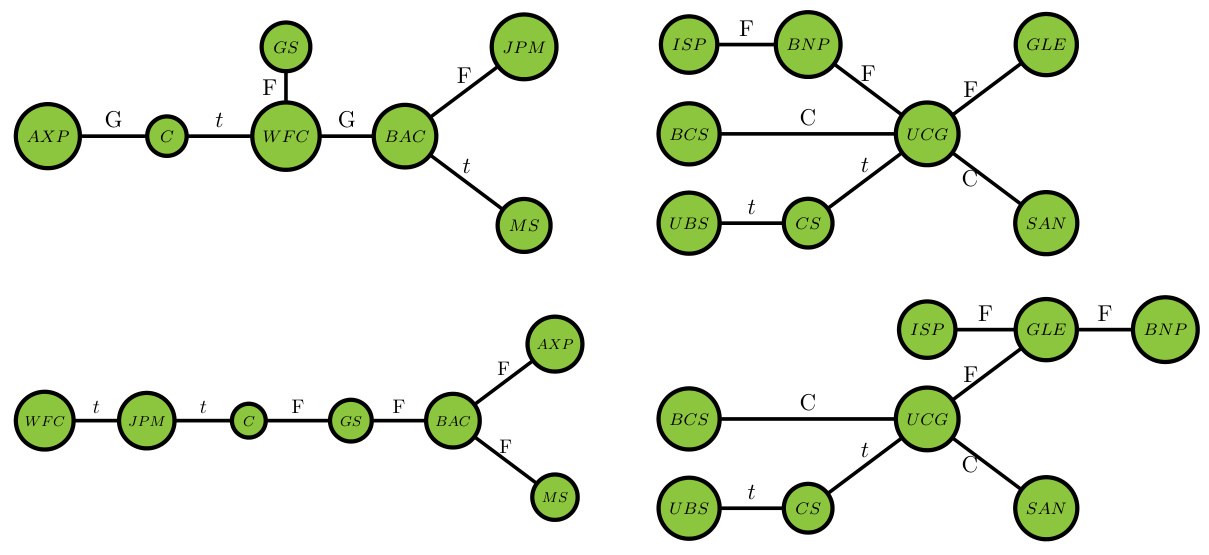
图9：系统性风险度量的滚动预测

---

总结

报告通过系统性和个体银行风险两条维度，利用先进的copula建模技术，搭建了一个高效而灵活的系统性风险分析框架，结合详实的欧洲与美国银行CDS市场数据，精确捕捉风险传染路径与极端风险爆发，实现对历次金融危机和系统濒危时期的准确定位与预测。理论与实证相结合，推广了因子依赖模型与变分贝叶斯算法在金融风险管理中的应用，为后续系统风险测度与监管提供了重要的工具和思路。

报告