• WIAE-GPF 结构与创新：采用弱创新表示理论，将复杂的非参数时间序列预测问题转化为无偏的IID均匀“伪创新”采样与解码过程，生成与未来真实条件概率分布一致的样本，实现了非高斯、非参数的时间序列概率预测，是对经典Wiener-Kalman滤波的广义推广。[page::5][page::8][page::13][page::14]

• WIAE训练机制：引入两个基于Wasserstein距离的生成对抗网络判别器，分别约束隐变量分布（创新判别器）及输入输出的分布一致性（重构判别器），采用因果卷积神经网络编码器和解码器联合训练，确保弱创新自编码器的有效学习。[page::11][page::12]

• 理论保证：证明了弱创新序列的贝叶斯充分性，确保基于其的预测无信息损失，且提出有限维度实现的结构收敛性定理，在理想训练条件下有限模型输出分布渐近于真实条件分布。[page::13][page::14][page::15][page::16]

- 多样化指标评估体系：采用NMSE、NMAE、MASE、sMAPE等多种点预测指标，CRPS、覆盖概率误差（CPE）、归一化宽度（NCW）等概率预测指标，全面评估预测精度和不确定性估计表现。[page::18][page::43][page::44]

• 实证评估：针对三个典型实时电力市场信号（NYISO的地点边际价格LMP，NYISO-PJM间LMP价差，PJM的区域控制误差ACE）进行了详细实验。结果表明：

- WIAE-GPF在夏季、秋季、冬季和春季的LMP预测中普遍优于DeepVAR、TLAE、Transformer系列（Pyraformer、Informer、BWGVT）和传统统计模型，CRPS和CPE指标显著最优，点估计指标也趋于更好。

- 对于跨ISO的LMP价差预测，WIAE-GPF在准确度（包含价格方向预测错误率PER）和概率指标均优于所有对比算法。

- PJM的ACE信号（15秒间隔）5分钟预测中，WIAE-GPF表现最佳，CRPS低于0.01，sMAPE低于11%，显著优于基于Transformer的BWGVT及传统方法。

• 量化因子 / 策略总结：

- WIAE-GPF的核心是构建弱创新自编码器，一方面通过编码器将时间序列映射为IID均匀分布的创新序列（隐变量），另一方面通过解码器利用隐变量和独立随机创新重构未来时间序列样本，实现条件概率分布的模拟。
- 训练使用同时最小化创新序列分布与均匀独立分布的Wasserstein距离，以及输入输出序列分布一致性的综合损失函数，保证模型拟合的有效性和泛化。
- 该方法具备贝叶斯充分性，确保从弱创新隐变量能无损推断未来变量，且有限维实现在训练充分下结构渐近逼近真实条件分布。

• 现场市场数据分析发现，实时电力市场信号（尤其LMP）表现出局部平稳性且长程依赖较弱（Hurst指数接近0.5），表明复杂长序列建模如大型语言模型(LLM)并无显著优势。实验中WIAE-GPF优于多种基于Transformer和LLM的模型，验证了创新表示非参数方法的有效性和实用性。[page::38][page::39]

金融/电力市场信号概率预测研究报告详尽分析

—— 对《Probabilistic Forecasting of Real-Time Electricity Market Signals via Interpretable Generative AI》报告的深度解析

---

1. 元数据与报告概览

• 报告标题：Probabilistic Forecasting of Real-Time Electricity Market Signals via Interpretable Generative AI

- 作者：Xinyi Wang, Qing Zhao, Lang Tong

• 机构：Cornell University电气与计算机工程学院

- 研究主题：利用可解释的生成型人工智能模型，对电力市场实时信号（如本地边际电价LMP、区域间价差、供需失衡等）进行概率性预测

• 核心贡献：提出了一种基于弱创新自编码器（Weak Innovation AutoEncoder, WIAE）的生成概率预测（Generative Probabilistic Forecasting，GPF）框架——WIAE-GPF。该架构不仅能够生成未来多变量时间序列的样本，且因其引入了创新序列的解释性表示，使得预测过程更透明且具备理论保证（训练充分时，生成样本分布与真实条件概率分布一致）。此外，对美国各地市场数据进行了多指标性能评估，WIAE-GPF在多个指标上优于经典和现有机器学习前沿技术。

- 报告核心信息传达：
- 生成式AI适合概率预测，传统方法受限于模型假设和参数化难题
- 利用经典时序表示理论可实现生成模型的可解释性与理论保障
- WIAE-GPF可作为基线，提升电力市场价格及相关实时信号的预测精度，对市场运营及风险管理极具价值

---

2. 逐节深度解读

2.1 摘要及引言部分（第0-3页）

• 观点总结：

- 生成式AI能模拟真实数据的内在结构，适合预测时间序列的条件概率分布
- 概率预测（PF）通常依赖参数模型简化无限维分布预测为参数估计，但面临模型不匹配风险
- 现有生成概率预测（GPF）方法多为参数模型，缺乏非参数的通用方案
- 本文首次提出基于弱创新自编码器的非参数GPF模型，解决了计算与采样复杂性
- 引入创新理论连接，保障模型的可解释性与生成样本的统计一致性
- 关联文献回顾涵盖经典的参数方法（ARMA、Gaussian等）、非参数的分位数回归、及近年深度生成模型（VAE、GAN、Transformer等），指出深度模型虽表现好但缺乏理论保障，大型语言模型（LLM）在电力价格预测中应用有限

• 关键点：

- PF和GPF的区别与联系：GPF直接生成未来样本，PF多依赖分布参数估计
- 创新表示理论根植于Wiener、Kallianpur、Rosenblatt等经典时序分析，为深度模型提供结构基础 [page::0,1,2,3]

---

2.2 WIAE-GPF模型介绍与原理（第4-8页）

• 核心论证：

- WIAE-GPF设计基于弱创新表示，提取时间序列中独立同分布的创新序列作为生成样本的隐空间
- 该结构是对经典Wiener/Kalman滤波的非高斯非参数推广，具备对应的因果编码器和解码器结构（见图1）
- 创新编码器类似因果白化滤波，解码器模拟线性预测过程
- 利用IID均匀分布的“伪创新”样本可生成满足真实条件分布的未来样本，实现有效采样
- 该方法具有理论保证：理想训练下生成样本分布收敛于真实给定历史的条件分布【定理1】；且对有限维网络实现收敛行为进行证明【定理2】

• 图1解读：

- 图示展示了编码器接收过去观测序列，生成创新序列，解码器结合来自均匀分布的伪创新生成未来样本
- 通过这种设计，WIAE-GPF实现了生成的随机样本真实反映未来多维时间序列的条件概率结构

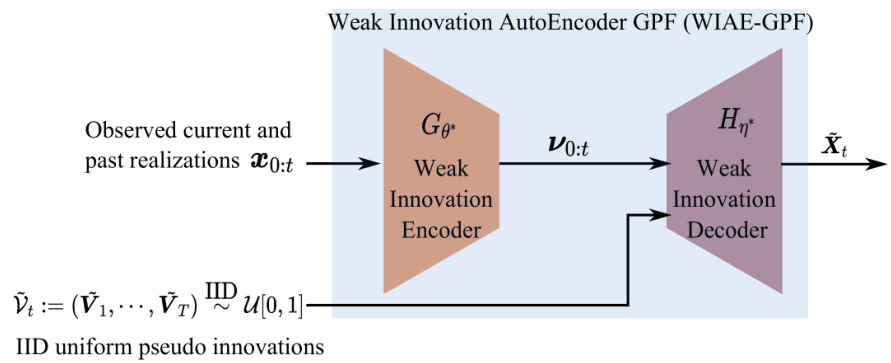
• 创新及可解释性亮点：

- 将经典统计学创新序列理论引入深度生成模型，保证生成过程不仅有效且解释明确
- 突破传统VAE对潜变量分布的高斯假设，采用非参数定义的弱创新约束
- 兼顾生成模型的灵活性与理论严谨性[page::4,5,6,7,8,10]

---

2.3 WIAE学习算法（第9-12页）

• 技术细节：

- 模型采用因果卷积神经网络构成编码器和解码器
- 采用两类Wasserstein距离判别器：创新判别器确保潜变量近似IID均匀；重构判别器保证重构分布与输入分布匹配（图3）

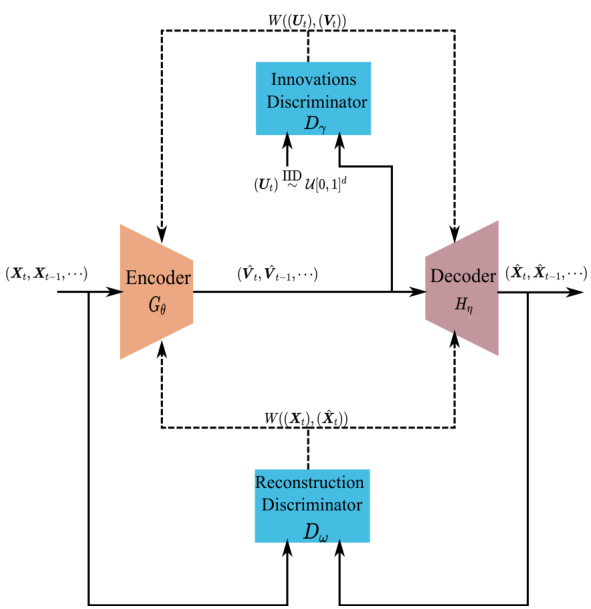
• 损失函数概览：

- 式(3)定义为判别器最大化与编码解码器参数最小化的min-max问题
- 结合两类Wasserstein距离，联合训练确保潜空间符号分布与输出重构分布的匹配

• 优势：

- 解决了传统强创新编码难以存在的问题
- 适应多维时间序列，避免单变量创新限制
- 去除参数化假设，适合复杂非高斯时序数据

• 训练细节：

- 采用Adam优化器
- 实际需基于有限时间窗口样本训练，后文分析有限维实现收敛性[page::9,10,11,12]

---

2.4 理论性质及概率生成（第13-17页）

• 贝叶斯充分性【引理1】：

- 证明创新序列作为统计量对未来时间序列具备充分信息，基于Markov结构，可无损决策

• WIAE-GPF有效性【定理1】：

- 给定训练后编码器-解码器，结合独立伪创新生成的样本，准确恢复了未来序列的条件概率分布

• 有限维实现的结构收敛【定理2】：

- 在训练样本无限及训练收敛条件假设下，有限输入维度的神经网络编码器解码器生成的预测分布，弱收敛至真实条件概率分布

• 衍生预测计算（点估计和分位数）：

- 提供通过Monte Carlo样本计算前向（MMSE均值）预测、中位数（MMAE）及任意分位数的方法

• 评价指标：

- 介绍多指标体系的选取，包含点预测（NMSE、NMAE、MASE、sMAPE）和概率预测指标（CRPS、CP、CPE、NCW）
- 解释各指标的物理意义及优势[page::13,14,15,16,17,18]

---

2.5 应用实验设计与基线技术（第19-24页）

• 应用范围：

- 三大电力市场信号：NYISO能源市场的实时LMP、NYISO-PJM间的LMP价差（CTS交易市场）、PJM调频市场的区域控制误差（ACE）预测

• 数据特征：

- 电价和ACE受内生市场调度影响，具有高波动性和尖峰特征
- 假设市场信号在短期具局部平稳性，适用于WIAE-GPF架构

• 基线方法：

- 传统参数模型 DeepVAR
- 变分自编码器类模型 TLAE
- 三种引入Transformer架构的大型语言模型（LLM）方法：BWGVT(结合分位数回归)，Pyraformer，Informer
- 统计分位数回归与经典机器学习方法

• 对比依据及准备：

- 数据集覆盖2023年不同季节，针对LMP季节性分析[page::19,20,21,22]

---

2.6 实验结果与分析：实时LMP预测（第24-32页）

• 季节与数据描述：

- 夏秋季波动剧烈，春季数据中存在极端异常峰值
- LONGIL节点LMP价格尖峰对预测有显著挑战

• WIAE-GPF表现总结：

- 在所有四季样本及指标中，WIAE-GPF均取得整体第一名或第二名表现，特别是在概率指标（CRPS、CPE）和NMSE优势明显
- 非参数特征使WIAE-GPF避免了传统模型的分布假设偏差，表现出更准确的条件分布匹配能力

• DeepVAR表现：

- 优于非参数的指标主要是中位数相关点预测（NMAE、MASE），表现出其对条件均值和媒值估计较好

• LLM模型表现：

- Pyraformer在寒冷季节NMSE表现优异，但整体点估计和概率指标不及WIAE-GPF
- Informer表现稳定，训练难度大且参数多，影响其性能发挥

• 异常点对评测影响的处理：

- 评价指标剔除距离均值3个标准差外的极端值，避免尖峰导致指标严重偏差

• 各季节模型轨迹可视化（图5、图6）：

- WIAE-GPF预测曲线紧贴真实走势，抑制波动过度，较少被尖峰影响
- 深度AR模型存在峰位错误，LLM模型偶尔波动较大而偏离真实

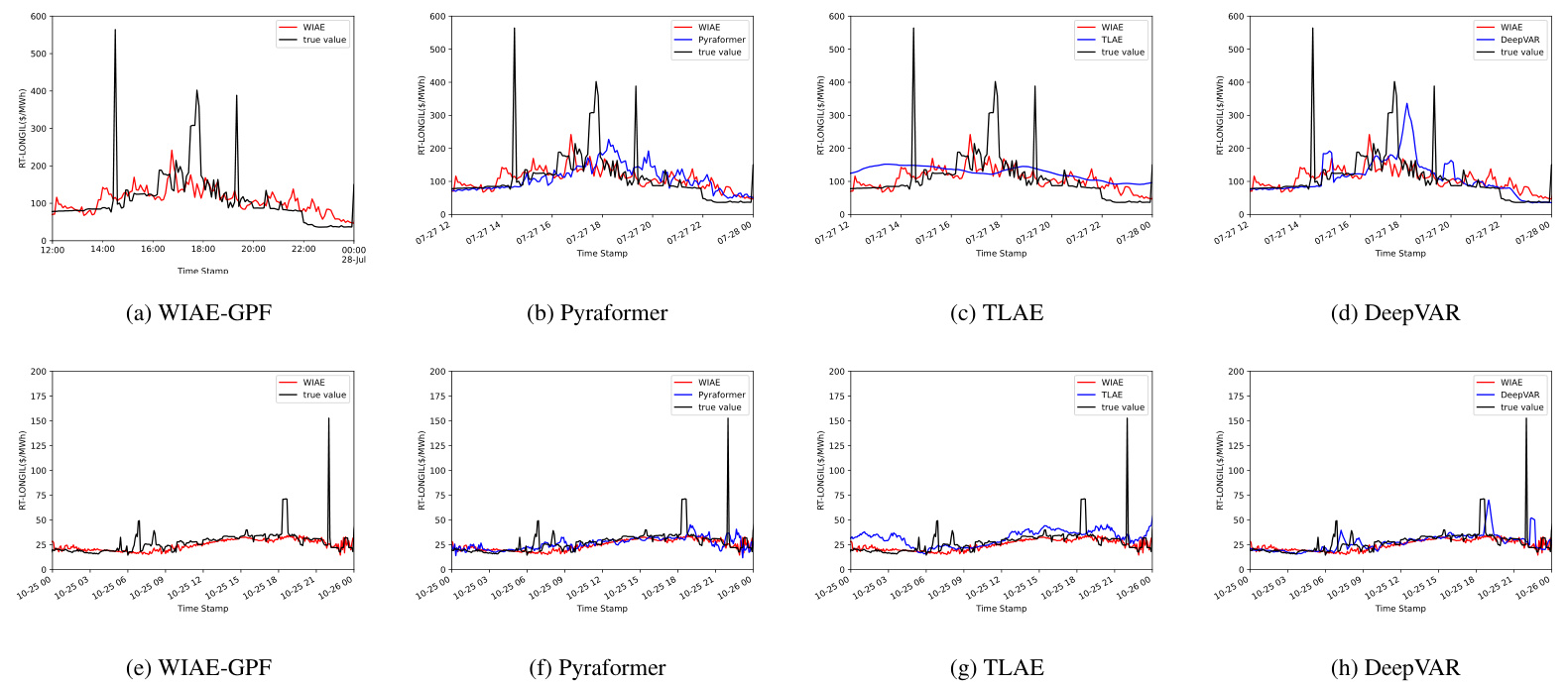
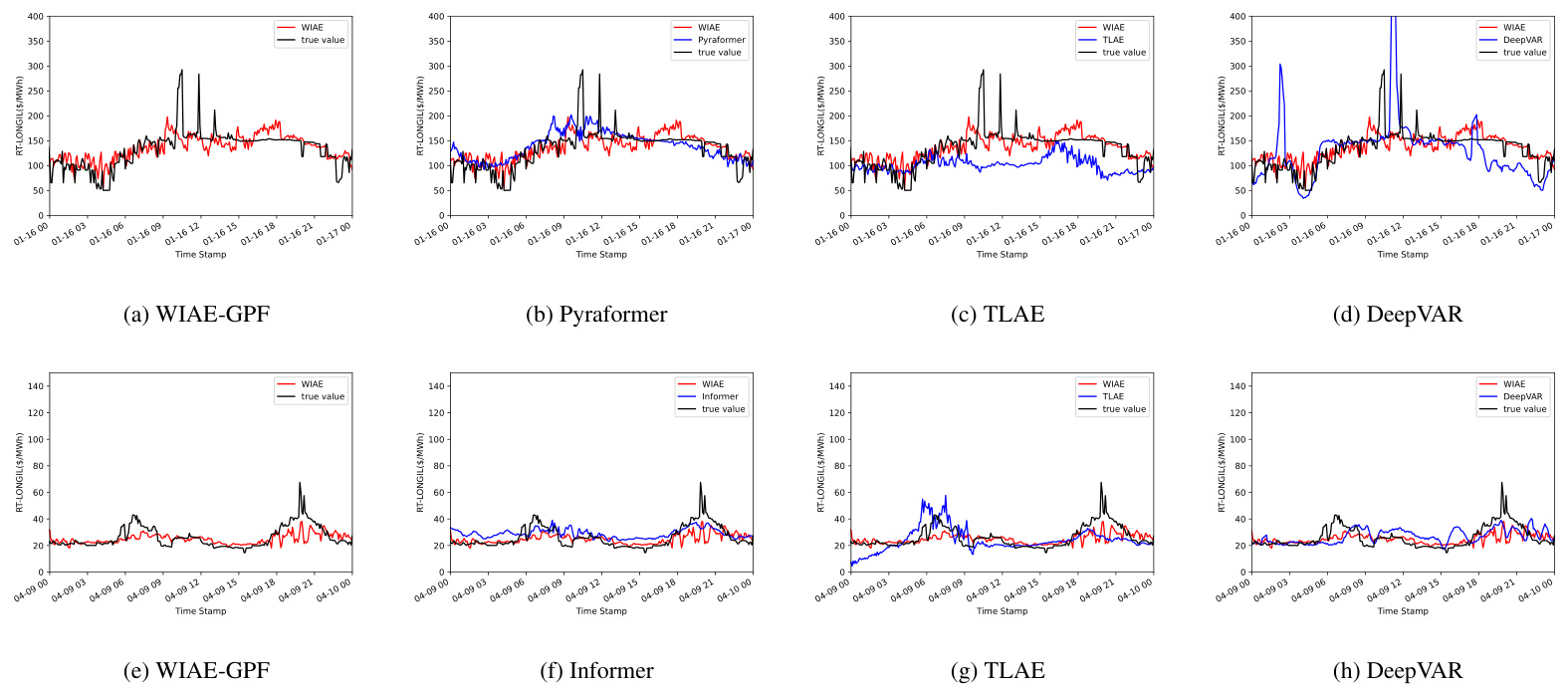
• 结论：

- WIAE-GPF非参数的优势、理论保证和创新编码示范了其卓越的市场价格预测潜力[page::23,24,25,26,27,28,29,30,31]

---

2.7 实验结果：区域间LMP价差与ACE预测（第33-37页）

• 区域价差预测：

- CTS市场用于虚拟交易，价差方向的准确预测至关重要
- WIAE-GPF在连续的数值指标及方向预测准确率上均优于其他方法
- TLAE量化回归（BWGVT）次之，LLM方法表现略逊
- 深度AR模型表现存在峰值错位和对快速变化反映迟缓的问题

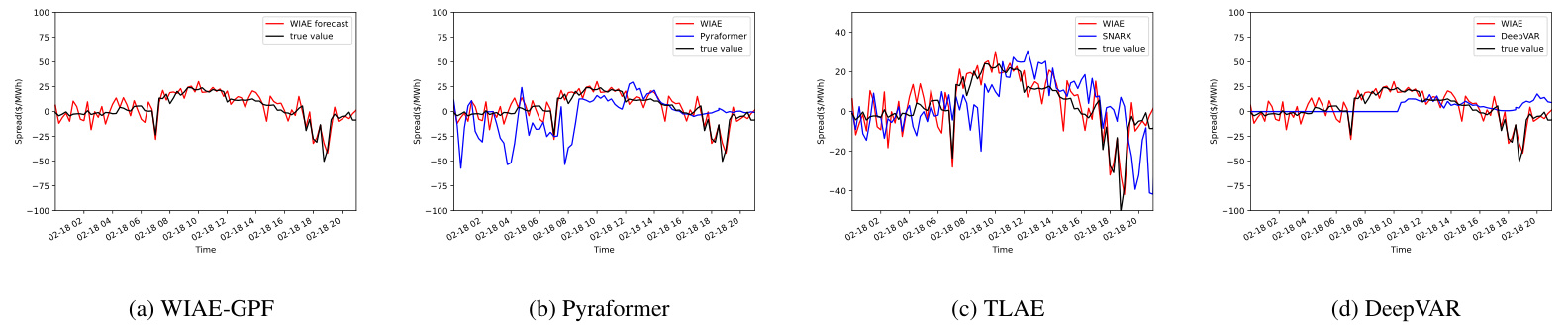
• ACE预测：

- 高波动性高频数据，5分钟提前预测难度大
- WIAE-GPF CRPS、sMAPE显著优于其他模型，表现稳定可靠
- BWGVT表现较差，区间宽度大，准确性较弱
- LLM预测NMSE较好，但整体NMAE和概率指标弱
- DeepVAR、SNARX表现落后，可能因模型不匹配产生较大误差

• 总结：

- WIAE-GPF对动态、高波动、复杂市场信号具有较强泛化能力，优于参数化及黑盒模型[page::33,34,35,36,37]

---

2.8 LLM技术讨论与长程依赖分析（第38-39页）

• 实证发现：

- LLM（Transformer及其变种）在电力市场信号中长程依赖特征较弱
- Hurst指数及去趋势波动分析均显示LMP信号长程依赖程度极低，接近随机游走或短程记忆
- 因此，LLM所擅长的长程依赖建模优势难以发挥
- WIAE-GPF通过创新序列捕捉关键新信息，虽不特意建模长程依赖，但效果优于LLM

• 基于此，作者推测电价信号的复杂度要求适合结构更简单且理论保障更强的模型

- 提示未来研究可结合跳变模型或非平稳方法拓展WIAE-GPF[page::38,39]

---

2.9 结论与未来展望（第39-41页）

• 研究三大贡献：

1. 开创性实现了非参数、具理论保证的生成式概率时间序列预测
2. 在真实电力市场数据上优于包括最先进LLM在内的多种前沿机器学习模型
3. 确立了弱创新序列的贝叶斯充分性质，理论与实践紧密结合

• 方法优势：

- 可解释架构，拟合传统Kalman滤波测量和预测更新过程
- 生成式AI与经典线性滤波的创新结合

• 局限性：

- 目前模型基于局部平稳假设，需扩展至非平稳时间序列（如用时变态势空间模型）
- 探索跳变过程和更复杂结构的未来改进方向[page::39,40]

---

3. 图表深度解读

图1 (第5页) WIAE-GPF预测管道结构

• 描述：展示了WIAE-GPF的核心机制——编码器从已观测序列生成创新序列，解码器结合IID均匀伪创新序列生成未来时间序列样本

- 解读：
- 编码器和解码器均是因果结构，确保生成过程符合时序关系
- 创新序列作为充分统计量携带所有未来预测所需信息

• 意义：

- 使整个生成预测过程具备严格概率含义，能够理论上保证生成样本分布的正确性[page::5]

图3 (第11页) WIAE训练架构

• 描述：展示了训练时编码器、解码器与两个对抗判别器的交互流程

- 解读：
- 创新判别器逼近编码空间潜变量与理想均匀分布
- 重构判别器保证预测分布与原始数据分布匹配

• 意义：

- 通过联合对抗训练，WIAE学习到满足弱创新定义的隐变量表示及对应解码结构[page::11]

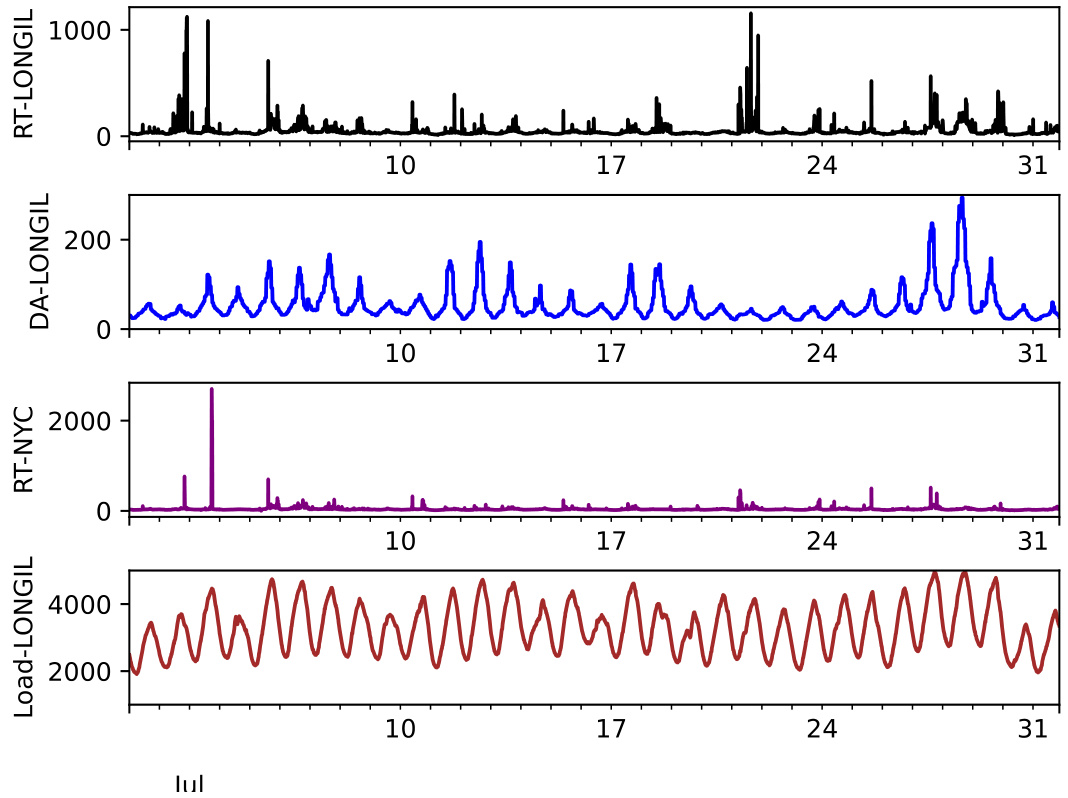
图4 (第21页) 7月LONGIL实时和日前负荷及电价曲线

• 描述：

- 包括实时LMP（LONGIL、NYC）、日前LMP（LONGIL）、以及负荷数据
- 时间跨度为整个月，间隔5分钟至1小时观测

• 解读：

- 实时LMP存在明显尖峰和高波动期，尤其在夏季7月
- 空间依赖显著，LONGIL与NYC间LMP相关性较强
- 负荷时间序列呈现季节性周期及波动特征

• 联系文本：

- 反映现实市场状态，证明预测复杂度和挑战，为模型评价提供背景[page::21]

图5 和 图6 (第29页, 30页) 不同月份LMP预测轨迹对比

• 描述：

- 与真实LMP轨迹对比，展现WIAE-GPF、Pyraformer、TLAE和DeepVAR等模型预测对比

• 解读：

- WIAE-GPF更准确跟踪真实价位，波动幅度适中，减小误差扩散
- 其它方法存在过度平滑或异常大波动，特别是深度AR和某些LLM

• 意义：

- 视觉验证WIAE-GPF具有更稳定、准确的预测，符合定量指标表现[page::29,30]

图7 (第35页) 州际LMP价差预测曲线

• 描述：

- 以NYISO-PJM间LMP价差时间序列为例，比较WIAE-GPF与Pyraformer、SNARX、DeepVAR预测

• 解读：

- WIAE-GPF预测和真实价差最为吻合，波动极小且捕获趋势明显
- 其他方法存在价格峰值错位及过度波动

• 联系文本：

- 强调非参数、创新编码方法对价差复杂动态有更好拟合能力[page::35]

图8 (第37页) PJM区域控制误差（ACE）轨迹

• 描述：

- 2023年1月24-26日3天内15秒分辨率的ACE时间序列

• 解读：

- ACE信号极具波动性，包含尖峰与快速变化

• 联系文本：

- 说明预测模型需能应对高频且噪声大的市场调控信号[page::37]

---

4. 估值分析

本报告未涉及传统金融估值分析，其核心内容围绕生成概率预测模型构建、验证及市场应用，没有传统意义上的企业估值、DCF或市值倍数分析。

---

5. 风险因素评估

• 模型风险及挑战：

- 依赖历史数据及局部平稳性假设，若真实市场非平稳变动剧烈，性能可能下降
- 神经网络训练依赖超参数与初始化，WIAE-GPF对其敏感度尚需进一步研究
- 尖峰和极端事件预测仍然挑战较大，模型对极端价格的捕捉依赖更多上下文信息

• 缓解策略：

- 通过贝叶斯充分性及结构收敛理论提供理论保障
- 使用多指标多季节测试，验证了模型一定范围内的鲁棒性
- 后续建议扩展非平稳及跳变过程建模能力，加强异常检测结合[page::39,40]

---

6. 批判性视角与细微差别

• 报告声称WIAE-GPF是首个非参数且有理论保证的GPF模型，但现实中，训练收敛与模型容量限制可能阻碍理论有效转化为实践效果

- LLM部分的劣势分析侧重于特定特征信号的长依赖性弱，未充分考虑可能通过微调和架构设计适应性提升的潜力

• TLAE和BWGVT表现偏弱，VAE设计与分位数回归的局限性未系统展开讨论

- 报告未深入探讨模型在异常波动和新兴市场条件（非静态市场环境）中的性能弹性

• 格外强调WIAE-GPF的可解释性，实质上仍为复杂深度神经网络架构，对于实时业务应用仍需进一步简化与验证[page::26,34,38]

---

7. 结论性综合

该报告系统提出并验证了创新编码自编码器的生成概率预测框架（WIAE-GPF），成功将经典时间序列创新理论与现代深度生成模型融合，填补了非参数生成概率预测领域的空白。WIAE-GPF既保证了预测结果的概率一致性，又兼备与Kalman滤波相仿的透明结构，为电力市场实时信号的多维时序预测提供了强有力的工具。通过美国NYISO和PJM市场实测数据展示，WIAE-GPF在多个点预测和概率预测指标上均优于DeepVAR、TLAE及多种LLM技术。

表格与图示深入反映了：

• LTC电价的波动性特征及空间时序关联性（图4）

- WIAE-GPF在季节性强和极端事件频出的环境下，稳定还原价格动态（图5、6）

• 价差与ACE预测场景下，WIAE-GPF的灵敏度、准确率和区间宽度整体领先（图7、8）

- 多指标客观评估体系支撑了结果的广泛适用性和鲁棒性

综上，WIAE-GPF既具有强理论基础，又展现了在电力市场高波动、非线性、非高斯环境下的卓越实用性，有望成为未来能源市场风险管理和调度优化的重要基础预测工具。未来工作重点聚焦非平稳过程扩展、异常事件刻画以及模型训练稳定性改进。

---

总体评价

本研究以严谨理论和丰富实证，首次实现了非参数且可解释的生成概率预测框架，有效增强了电力市场时序数据的预测能力。其新颖创新编码视角值得业界关注和后续推广。报告结构清晰，理论与实践结合紧密，指标选用严谨，图表展示直观，对相关领域科研及实际应用均具深远指导意义。[page::0~53]

---

如需进一步数据或章节解析，欢迎继续交流。

报告