亚梯度与模拟退火混合算法设计 [page::2][page::5]

• 将局部搜索的亚梯度法与全局搜索的模拟退火法结合，解决非光滑非凸优化问题。

- 算法交替执行：用亚梯度方法寻找驻点，用模拟退火跳出局部最优，提升全局最优搜索能力。

• 证明算法在有限步内收敛到可接受的$(\eta,\delta)$-驻点。

半变分不等式与接触力学建模 [page::6][page::7]

• 以弹性体静力接触为背景，构建基于子微分的接触条件及力学平衡表达。

- 将问题转换成带非光滑非凸势能函数的优化问题，利用有限元离散求解。

实例应用及数值验证 [page::8][page::9][page::10][page::11]

• 针对多层复合材料接触梁模型进行了仿真验证，考察不同层数和载荷下的力学响应。

- 提供了功能非单调的接触势能$j(u)$曲线，表现材料分层断裂引起的非线性响应。

• 比较六种优化算法，亚梯度与混合亚梯度方法在求得全局最优及计算效率上优于基准算法Powell及BFGS类方法。

- 模拟退火结合亚梯度显著提升全局最优搜索能力，避免陷入局部极小点。

方法贡献与创新点总结 [page::5][page::12]

• 结合亚梯度方法的非光滑处理能力与模拟退火的全局搜索特性，形成新型混合优化框架。

- 数学上给出收敛性及算法终止的理论保证。

• 展示用于复杂材料接触力学中的良好性能，支持多层非凸复合材料的数值模拟。

详尽全面分析报告：《Hybrid subgradient and simulated annealing method for hemivariational inequalities》

---

1. 元数据与概览

报告标题： Hybrid subgradient and simulated annealing method for hemivariational inequalities

作者及机构：

• Piotr Bartman-Szwarc（Jagiellonian University, 波兰）

- Adil M. Bagirov（Federation University Australia）

• Anna Ochal（Jagiellonian University, 波兰）

日期： 未明确指明，文中引用较新资料至2022-2023年左右。

研究领域及主题：
该论文聚焦于半变分不等式（Hemivariational Inequalities, HVI）的数值解法，尤其针对由接触力学问题衍生的非光滑非凸优化模型。提出一种结合局部子梯度法（subgradient method）与全局模拟退火法（simulated annealing）的混合算法，用于求解这类具有复杂非光滑、非凸特性的优化问题。

核心论点与贡献：

• 针对HVI问题中的非光滑非凸能量函数，提出一种全局汇聚的聚合子梯度方法，通过结合模拟退火算法，实现从局部最小值跳脱，从而实现更优全局最优解的搜索。

- 设计并实现包含“空步”和“实步”的算法结构，空步使用有限的两个子梯度决定搜索方向，实步则为参数更新步骤。

• 通过典型的接触力学问题案例验证算法性能，并与现有数值算法比较，展示了该混合方法的优势。

[page::0,1,5]

---

2. 逐节深度解读

2.1 引言 (Section 1)

• 论文从半变分不等式的一般背景入手，指出HVI为变分不等式的推广，通常与非光滑非凸能量函数的亚稳点问题等价。

- 文献回顾了HVI的应用范围，特别是接触力学领域，以及已有的求解方法。

• 明确了本文的目标——开发一种兼顾非光滑性（通过子梯度法）和非凸性（通过模拟退火）结合的数值算法。

- 强调该方法在寻找能量函数的亚稳点的同时，通过模拟退火跳出局部极小值，以期获得全局最优解。

[page::0]

2.2 子梯度法基础与算法设计 (Section 2)

• 问题定义：

目标函数为
\[
\mathcal{L}(\mathbf{u}) = \frac{1}{2}\langle A\mathbf{u}, \mathbf{u}\rangle + \langle \mathbf{b}, \mathbf{u}\rangle + J(\mathbf{u}),
\]
其中 \(A\)是正定对称矩阵，\(\mathbf{b}\)是向量，\(J\)为非光滑非凸的局部利普希茨函数。

• 重要假设包括对函数 \(\mathcal{L}\) 的亚梯度定义及对差分约束的限制，保证能应用埃克分解与子梯度概念。特别强调\(J\)可视为差分凸（DC）函数的典型代表。
• 算法结构：

设计了双循环的迭代算法——内循环（计算搜索方向）和外循环（更新步长参数 \(\eta\)）。通过“聚合子梯度”(aggregate subgradient)构建方向，使用两个子梯度的凸组合，保证了下降条件和收敛性。

• 收敛性理论支撑：

- 证明了内循环有限步终止性，基于对更新子梯度序列的单调性与有界性分析，控制了迭代次数的上界（相关公式详见页2-4）。
- 定义了\((\eta, \delta)\)-站点，并证明算法在有限步骤内能找到该近似站点。
- 采用数学归纳和反证法，保证目标函数有下界时，算法不会无限下降。

[page::1,2,3,4,5]

2.3 混合算法设计：结合模拟退火 (Section 2末尾)

• 定义了Metropolis函数作为模拟退火中的接受概率函数。
• Algorithm 2描述了完整的混合流程：

1. 以初始点开始用算法1找到局部稳点。
2. 用模拟退火生成随机扰动，尝试跳出局部极小。
3. 如果新点更优，则更新最佳点。否则，以一定概率接受新点，避免陷入局部极小。
4. 轮回迭代，持续搜索可能的更优起始点。

• 该方法的理论优势为根据已知模拟退火收敛性质，可以保证算法几乎必然收敛至全局最优解。

[page::5]

2.4 接触力学问题描述 (Section 3)

• 详细介绍了弹性体在二维/三维空间中占据的域、边界划分以及边界条件。关键的物理量有拉伸应变\(\varepsilon(u)\)、应力\(\sigma\)、位移\(u\)、与接触边界的单位法向量。
• 通过多物理场的边界值问题建立起半变分不等式形式(HVI)，说明了一般接触力学问题的数值求解等价于求解该HVI。
• 列出了本问题的基本假设：

- 弹性算子\(\mathcal{A}\)满足对称性和正定性。
- 接触势\(j\)满足局部利普希茨连续性、有界子梯度和半变分不等式必要的单调性及光滑性条件。

• 将空间问题利用有限单元法离散化，从而得到有限维的优化问题，形式对应前述的数学优化模型。

[page::6,7]

---

3. 图表深度解读

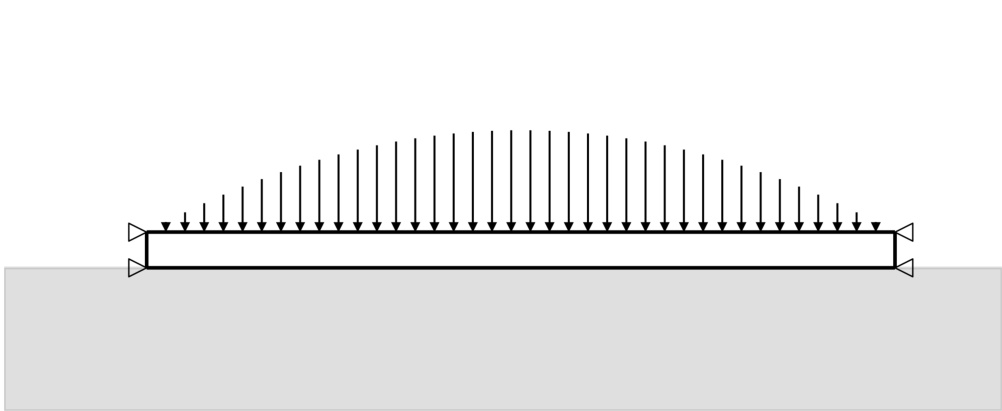
3.1 图1：二维梁模型示意

该图展示了受力梁结构，长度210mm，厚度10mm，两端固定，中间承受分布向下压力，梁直接接触软基底。

• 该示意图明确了模拟的物理边界条件及施加载荷分布，是后续数值模拟的基础。

- 图中箭头量化了施力方向和分布，为能量函数定义提供外力输入。

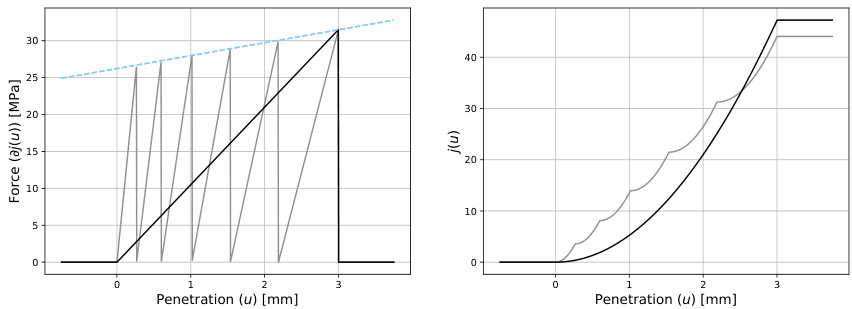
[page::8]

3.2 图2：非单调接触律及其能量函数表现

左图展示了接触力-渗入深度关系的非单调性：

• 黑线代表两层复合材料的响应，力随渗入深度线性增加至临界点，临界点后因保护层破裂，反力骤降；

- 灰线代表七层更复杂复合材料的逐层裂解，呈多阶梯形非光滑力响应。

右图是对应的能量函数 \(j(u)\)，显示明显的非凸非光滑特征，且层数更多时曲线更复杂。

• 该图形象展示了问题非光滑非凸的本质，验证了算法设计针对复杂接触力学材料的必要性。

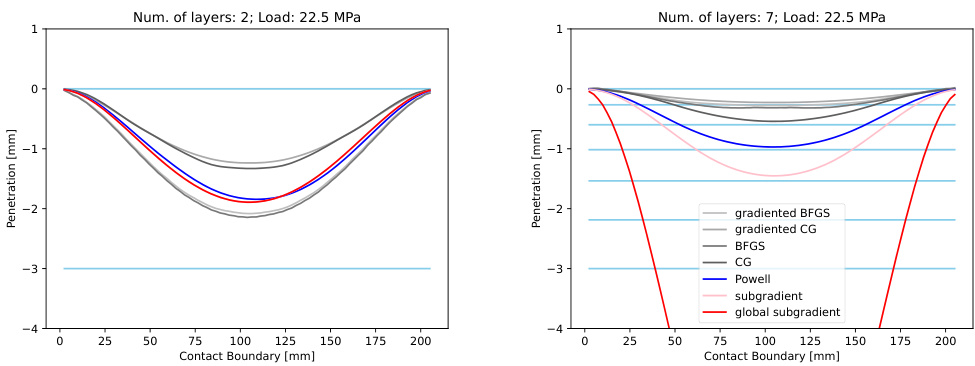
[page::9]

3.3 图3：梁的形变（渗入深度）比较

• 左图为2层保护层，右图为7层复合层情况下的渗入深度分布。

- 多条曲线对应不同数值优化方法：包括BFGS、共轭梯度法（CG）、带子梯度的梯度方法、Powell方法、基本子梯度法和本文提出的全局聚合子梯度法。

• Powell法表现良好但计算量大；常规梯度法虽然快但结果不好；基于子梯度的全局搜索子梯度法达到较佳的解且收敛更稳健。
• 位置与曲线细节揭示出层数越多，非线性越强，局部极值陷阱越多。

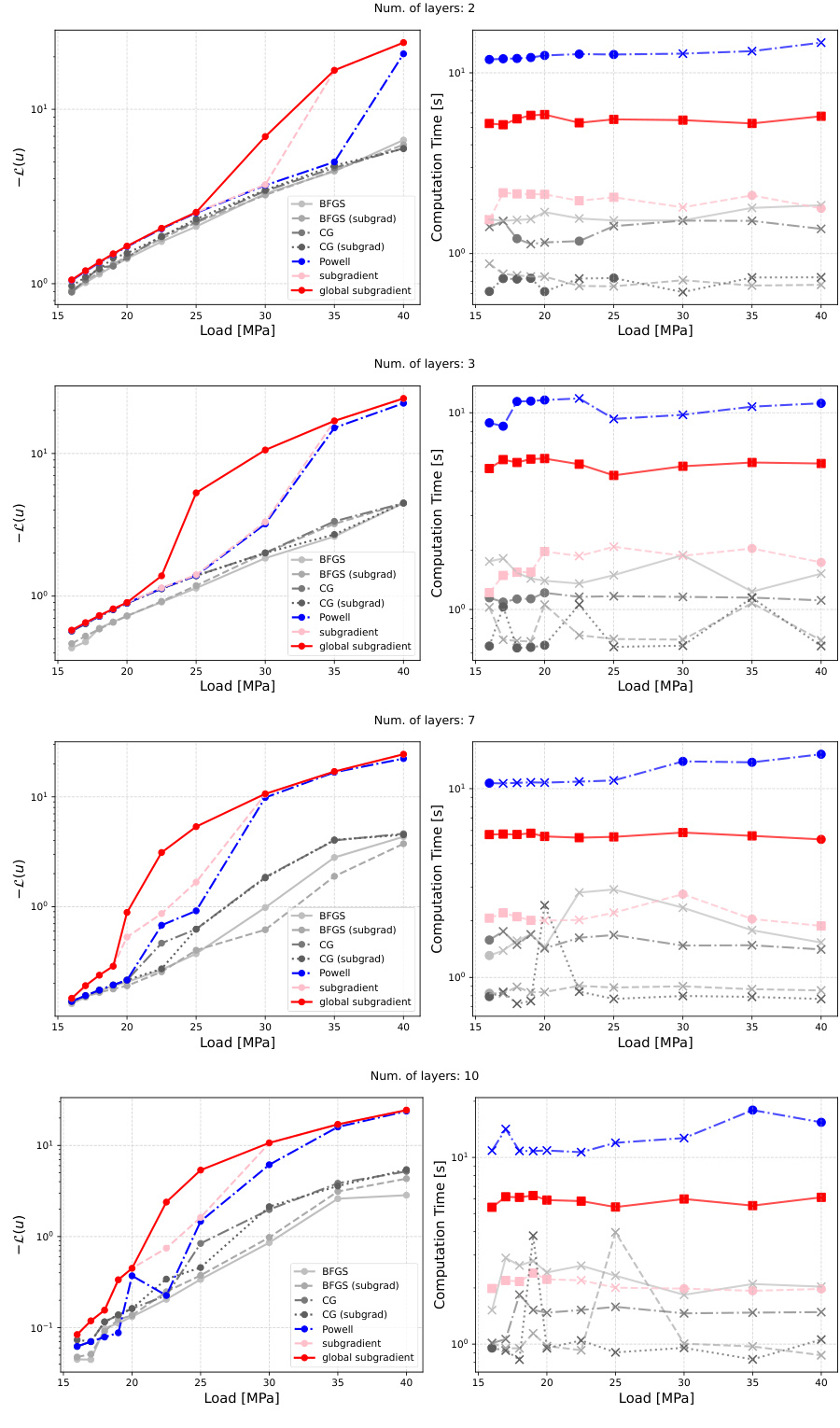
[page::9]

3.4 图4：优化过程中的能量函数值与计算时间

• 左侧图表为负能量函数值（以便更大值表示更优解），纵轴为对数尺度。

- 不同图表分别对应层数为2、3、7、10的复合材料。

• 标记符号：

- 方块：该方法中找到的最优值
- 圆点：接近最优（在0.9倍最优值以上）
- “×”符号：较差结果

• 右侧为对应计算时间，单位秒。

解读：

• “global subgradient”方法在准确性与计算效率上均优于其他算法，尤其在层数较多时优势更明显。

- Powell方法虽精度高，但时间开销是全局子梯度法的数倍以上，且容易陷入中间状态。

• 传统梯度和共轭梯度方法整体表现一般，且污染较多噪声点。
• 这些数据表明，本文提出的混合子梯度-模拟退火方法兼具全局搜索能力与非光滑处理优势，适合复杂接触力学问题。

[page::10,11]

---

4. 估值与算法分析

本报告并无典型金融估值模型，所讨论为数学优化算法。不过可归纳算法的性能评估：

• 目标函数为非光滑非凸复合能量函数（带形式 \(\mathcal{L}(\mathbf{u})\)），多局部极小值，传统方法难以保证全局最优。

- 子梯度法：允许处理非光滑性，保证向亚稳点收敛。

• 模拟退火法：通过概率接受非优解跳出局部极值，保证全局收敛概率为1。

- 混合方法设计，在维持局部搜索效率的同时，增强全局探索能力。

算法复杂度未详细量化，但通过数值实验比较，混合方法在计算时间与结果质量间取得较好平衡。

---

5. 风险因素评估

论文涉及的风险主要为算法效率及可靠性风险：

• 非光滑非凸的优化问题固有复杂，可能陷入局部极小状态，降低算法有效性。

- 模拟退火策略中参数（温度、退火速率等）对性能影响不确定。

• 算法终止条件、步长选取不当可能影响收敛速度或结果准确性。

- 数值离散化、网格尺寸等对计算精度与复杂度的权衡。

论文通过数学证明及数值验证，从理论和实践两方面缓解上述风险。

---

6. 批判性视角与细微差别

• 文中数学收敛理论建立在若干理想假设（如函数局部利普希茨连续、目标函数有下界）。实际问题中若这些条件不满足，可能影响收敛保证。

- 模拟退火方法在实际执行时依赖降温策略和参数调节，算法表现对于这些设置较为敏感，论文未详细展开敏感性分析。

• 数值例子基于二维简化模型，三维或更复杂模型的计算复杂度及收敛性可能变差，需进一步验证。

- 多层复合材料的模型近似性质也可能影响结果的真实反映。

• 总体而言，方法理论充分，实验验证有力，但在实际复杂工程应用中仍需根据具体情形调参。

---

7. 结论性综合

本文针对接触力学中由半变分不等式形成的非光滑非凸优化问题，提出了一种混合子梯度与模拟退火法。该方法具有以下亮点和贡献：

• 结合两种算法优势，子梯度法负责局部快速下降与稳点发现，模拟退火法用以跳出局部极小值，提高全局搜索能力。

- 数学上证明了算法在有限步内找到近似站点，并结合模拟退火保证全局收敛概率为1。

• 通过二维弹性梁接触复合材料的非单调接触问题数值实验，展示了该算法在处理非凸非光滑能量函数时的优越性。尤其在层数多的复合材料接触问题上，展现出高精度与较高的计算效率。

- 与传统梯度类方法、Powell方法比较，混合算法在准确率和计算速度间达到较优平衡。

• 数值工具包conmech使用Python实现，并结合编译加速(Numba)，具备实用性和扩展性。

综上，本文工作有效推进了HVI数值优化的算法研究，尤其适合接触力学领域复杂材料的模拟，具有理论价值与应用前景。

---

参考溯源

本文分析内容对应原文页码如下：

• 引言与方法设计：[page::0,1,2,3,4,5]

- 接触力学建模：[page::6,7]

• 数值实验与图表：[page::8,9,10,11]

- 结论与文献：[page::12]

---

总结

本文对半变分不等式的非光滑非凸优化问题提出了一种创新的混合算法，理论严密，数值验证充分。对相关领域研究者和工程师均具有较强参考和指导意义。

报告